基于球面投影的散乱点云三维建模算法实现与效果分析

徐秀川,花向红,龚子桢,郝 旦

(1.武汉大学 测绘学院,湖北 武汉 430079;2.武汉大学 灾害监测与防治研究中心,湖北 武汉 430079)

基于球面投影的散乱点云三维建模算法实现与效果分析

徐秀川1,2,花向红1,2,龚子桢1,2,郝 旦1,2

(1.武汉大学 测绘学院,湖北 武汉 430079;2.武汉大学 灾害监测与防治研究中心,湖北 武汉 430079)

介绍基于球面投影的散乱点云三维建模算法步骤,运用VC++编程语言结合OpenGL图形接口实现该算法,并结合实例说明球面投影法相对于圆柱面投影法、椭球面投影法在三维建模中的优势。

球面投影法;散乱点云;Delaunay三角网;三维建模

三维激光扫描技术是目前测绘领域中一个新的研究热点,其中散乱点云数据建模主要采用基于体剖分、基于面剖分和基于面投影3种方式建立。基于面投影是先将三维空间数据投影到平面上进行平面构网,再映射到三维空间最终达到三维建模目的。这种方法相对于基于体剖分和基于面剖分构造三角网出错率较低,构网效率相对较高。而基于面投影法分为基于平面投影、临近区域切平面投影、圆柱面投影法。平面投影法只适用于平坦点云;临近区域切平面投影处理复杂的点云时,生成的格网有重叠现象,不利于结构复杂的大型点云的数据处理;由于圆柱面投影法是将空间点沿着半径方向投影到圆柱面上,顶部和底部数据点的投影易产生重叠,无法维持点云中原有的点之间的相对位置关系。针对圆柱面投影法的缺陷,曹操提出椭球面投影法,该方法是沿着椭球中心将各点投影到椭球面上,这就避免了点的重叠,然后根据高斯投影投影到平面上,在平面上构造Delaunay三角网后再映射成三维空间三角格网。椭球面投影虽然避免了圆柱面投影的缺陷,但是由于该方法需要涉及到迭代计算,且正算公式复杂,应用椭球面投影法建网效率明显低于圆柱面投影法,且随着点数的增多,这种差异越明显。为此,本文从提高椭球面投影效率的角度出发,提出球面投影法。详细论述了基于球面投影的散乱点云三维建模算法步骤,并结合实例证明球面投影法相对于圆柱面投影法、椭球面投影法在三维建模中的优势。

1 基于球面投影的散乱点云三维建模的实现

基于球面投影的建模方法的基本思路是:经过数据配准[1],由三维激光扫描仪获得的点云原始坐标都转化为统一空间坐标系下的坐标(Xi,Yi,Zi)。以球面为媒介将空间散乱点云(Xi,Yi,Zi)投影到平面上,得到相应二维坐标(xi,yi),在平面内通过Delaunay算法构造平面三角网,最后将平面三角格网映射到空间完成三维建模。

1.1 散乱点云投影到平面

图1为球面坐标系,O为球心,且尽量定位在扫描对象的几何中心,球的半径 r大小可根据计算简便需要任意选择,OX、OY、OZ轴构成右手坐标系,投影方向沿着球心指向各点。

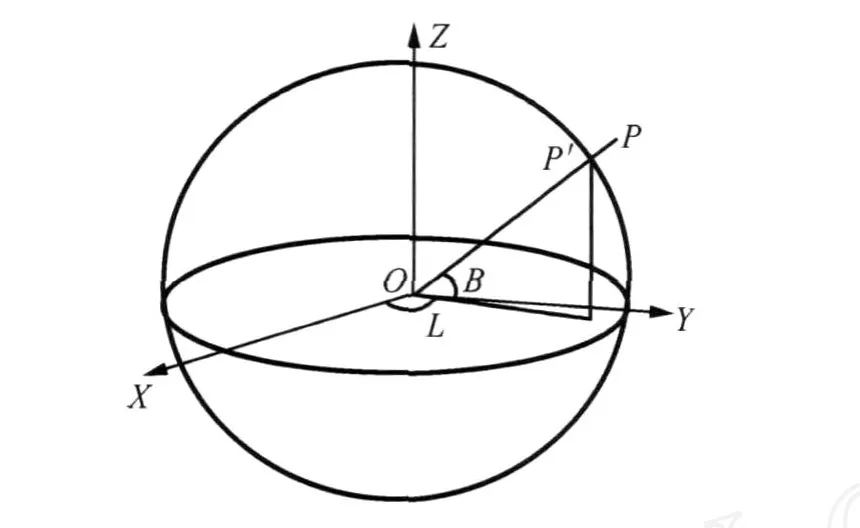
图1 球面坐标系

设 P(X,Y,Z)为任一点云数据,经投影后在球面上有唯一的 P′与点 P对应。球面坐标用(L,B)表示,与大地测量中大地经度与大地纬度定义类似,L表示OP′连线在XOY平面上的投影与OX轴的夹角(0°＜L≤360°),B 表示直线 OP′与 XOY面的

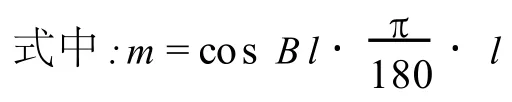
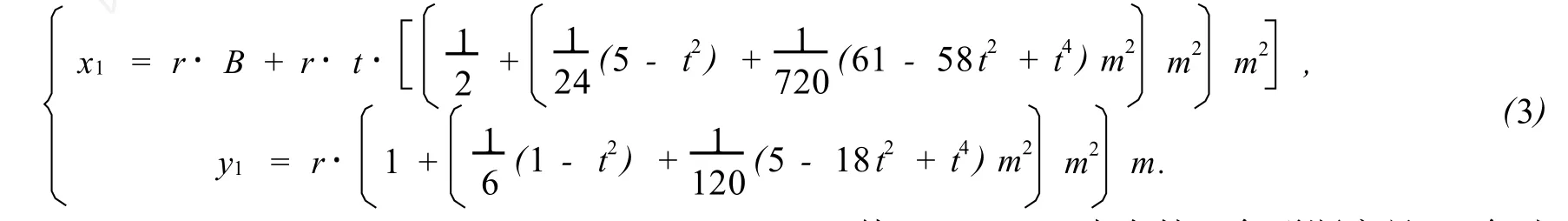
为大地经度与中央子午线的差值;t=tan B,r为球半径。

虽然扫描对象不像地球那样庞大,但考虑到计算结果的准确性,从尽量减小变形的角度出发,仍然对球面进行分带投影,选用6度带投影。然而不同带的点通过正算式(3)获得的平面坐标并不在同一个平面直角坐标系中,这样就不能保证点与点之间原有的相对位置关系,通过式(4)可将计算所得的平面点归化到统一坐标系中。x、y为归化后的坐标。

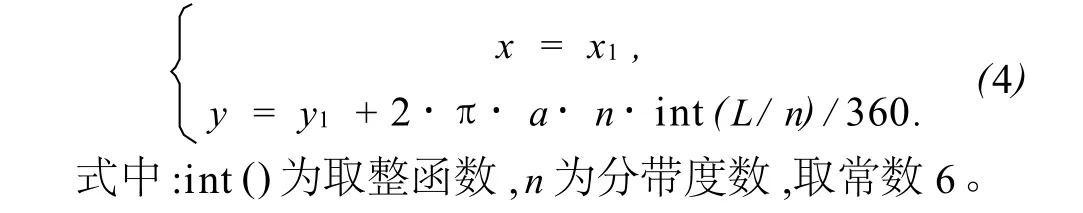
1.2 Delaunay生长算法构造平面三角网

经过以上各步骤的投影后,就将空间点云数据投影到统一的平面坐标系中,根据各平面点坐标(xi,yi),可由Delaunay生长算法构造平面三角网。其基本步骤如下:

1)创建点point表,边list表,三角形 triangle表,point表存储各点坐标信息及顺序点号,list表存储边号、两个端点点号、对面点点号以及各边的usetime值。Triangle表存储三角形顺序号、三条边顺序号。

2)构建初始基线:在点point表中选择顺序点号点为1的点 A作为初始点,然后遍历所有点,找到距点A最近的点B,连接后作为初始基线。将该边放入边表edge中,并将该边的usetime值设为1。如图2(a)所示。

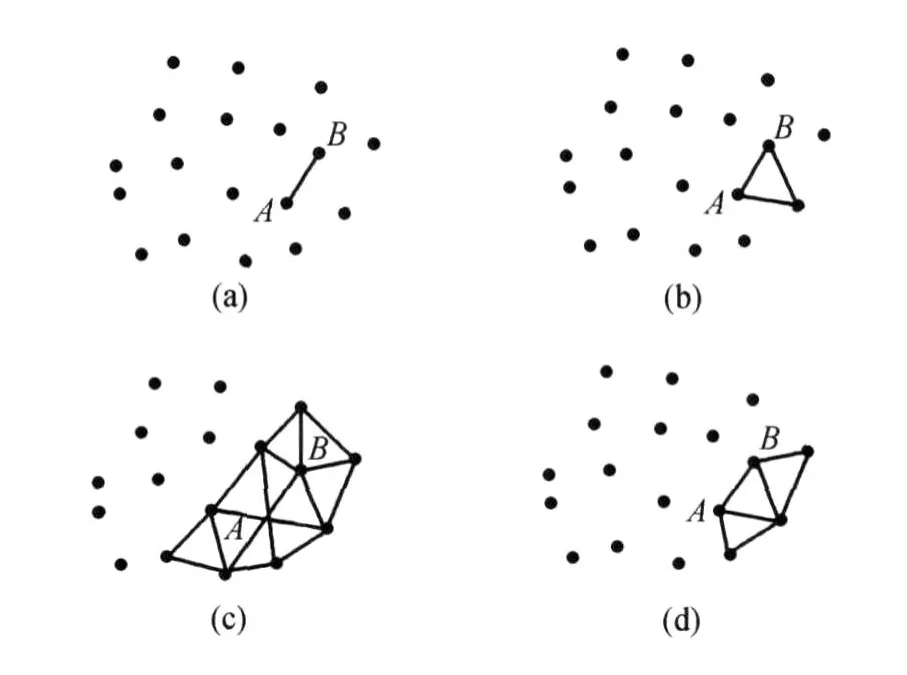
图2 Delaunay生长算法示意图

3)构建核心三角形:运用Delaunay法则搜寻第3点,具体的做法是:遍历所有点,查找距此初始基线距离最短的点,可由余弦定理求该边对应角最大的点为第3点。将新形成的两个边放入边表list表尾,边usetime值均设为1,三角形放入三角形列表triangle中。如图2(b)所示。

4)扩展核心三角形:由核心三角形的各边分别向外扩展新的三角形,具体做法是:在该扩展边在原三角形中的对应点异侧的所有点中,如步骤2)按照余弦定理查找与该边对应角最大的点,并组成新的三角形,加入 triangle表尾,两条新边加入 list表尾,usetime值设为1,已扩展的初始边usetime值变为2。如图2(d)所示。

5)在list表中依次按步骤3)扩展所有usetime值为1的边,扩展后usetime值变为2,扩展的新边顺序放到edge表中,usetime均设为1,新三角形加入triangle表中。

6)重复步骤3)、4),直至边表中所有边的 usetime值变为2,或usetime值为1的边无法再找到满足扩展要求的点。

7)三角格网优化:根据最小内角最大准则,对所建成的三角格网进行优化。

1.3平面三角格网映射为空间三角格网

由于投影前后保证了点的相对位置不变,且点表中包含点号信息,将三维点按照平面三角格网确定的拓扑关系根据点号进行连接,可以将平面三角格网映射为空间三角格网,实现空间建模。

2 程序实现与效果分析

根据上述所介绍的基于球面投影的散乱点云三维建模步骤,运用VC++编程语言结合OpenGL图形接口实现。

2.1 球面投影法与圆柱面投影法效果分析

选取皇冠模型原始数据(共含14443个点云数据),如图3所示,分别采用圆柱面投影法与球面投影法进行建模,圆柱参数底面圆半径 R=1,球参数半径 r=1。其建模效果见图4、图5。

图3 散乱点云

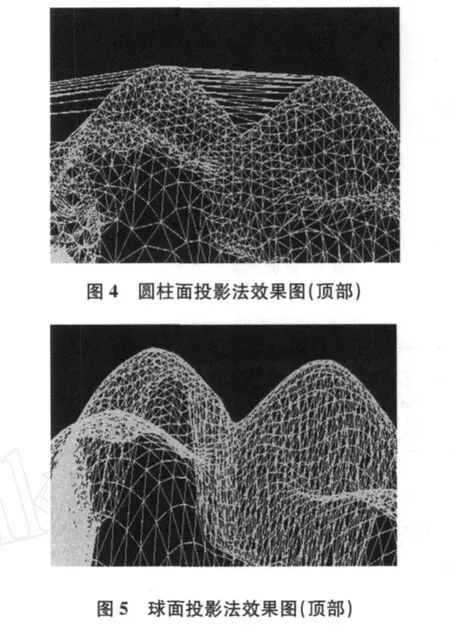
由图4、图5可以看出:对于顶部的点云利用圆柱面投影实现空间建模时,顶部点云格网拓扑关系较混乱,而利用球面投影法生成的三角形的形状较为均匀,网形结构较为合理,能较好地维持原始的拓扑关系。可见,球面投影法很好地弥补了圆柱面投影法由于投影方式造成的顶部数据投影重叠这一缺陷,可以更好地维持顶部或底部点云的拓扑关系。

2.2 球面投影法与椭球面投影法效果分析

同样选取图3所示点云数据,分别采用椭球面投影法和球面投影法构造空间三角格网,椭球面投影法椭球参数长半轴 a=2,短半轴 b=1,球面投影法球参数半径 r=1。图6为椭球面投影法建模效果局部截图,图7为球面投影法建模效果局部截图。为了更好地进行效率对比,从原始点云中任意抽取1132、3842个点云数据,分别采用椭球面投影法和球面投影法进行建模,并记录完成时间,实验结果如表1所示。

图6 椭球面投影法效果图(局部)

图7 球面投影法效果图(局部)

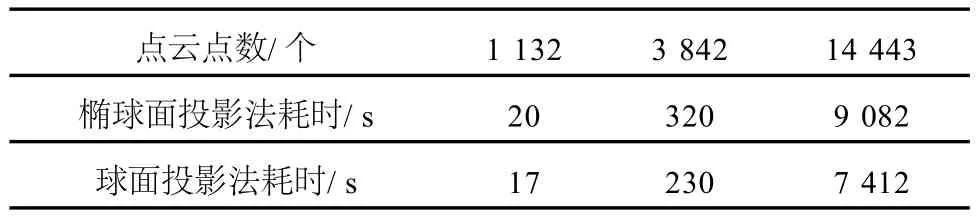
表1 点云数据建模效率对比

由表1可以看出:对于相同数量的点云数据,利用球面投影法构造三角格网速度更快,且点云数量越多,这种优势越明显。由图6和图7效果对比可以看出:对于较平坦区域,椭球面投影法与球面投影法效果类似,但对于表面曲率变化较大的区域,球面投影法比椭球面投影法构造三角网出错率更低,建模效果更好。由于球的特殊性,球面投影相对于椭球面投影,投影间的转换公式简单且精确,采用球面投影法建模效率更高,且效果更好。

3 结束语

实验结果表明,基于球面投影的散乱点云三维建模方法,可以避免圆柱面投影过程中造成的顶部或底部点云数据缺失问题,同时,在建模效率及效果方面,球面投影法也优于椭球面投影法。球面投影法具有很好的实用价值。

[1]曹操.三维激光扫描数据三角格网建立方法的研究[D].南京:河海大学,2008:33-35.

[2]郑德华.三维激光扫描数据处理的理论与方法[D].上海:同济大学,2005:64-70.

[3]孔祥元,郭际明,刘宗泉.大地测量学基础[M].武汉:武汉大学出版社,2005:156-158,103-104,108-109,112-113.

[4]武晓波,王世新,肖春生.Delaunay三角网的生成算法研究[J].测绘学报,1999,28(1):28-35.

[5]江剑霞,刘少华,吴汉英.VB环境下不规则三角网的算法设计与实现[J].四川测绘,2006,29(2):64-67.

[6]蒋红雯,涂鹏,李国忠.基于生长算法构建Delaunay三角网的研究[J].公路交通科技,2004(12):38-40.

The im plementation algorithm of three-dimensionalmodeling to point cloud based on spherical surface projection and effect analysis

XU Xiu-chuan1,2,HUA Xiang-hong1,2,GONG Zi-zhen1,2,HAO Dan1,2
(1.School of Geodesy and Geomatics,Wuhan University,Wuhan 430079,China;2.Research Center for Hazard Monitoring and Prevention,Wuhan University,Wuhan 430079,China)

The algo rithm of three-dimensional modeling to point cloud based on spherical surface p rojection is introduced in the paper,and the algorithm is achieved through the app lication of VC++combining graphical interfaces OpenGL,and the superiority of spherical p rojection methods against the cylindrical p rojection methods and ellipsoidal p rojection methods is demonstrated by instance.

spherical p rojection methods;point cloud;Delaunay triangulation netwo rk;three-dimensional modeling

TP309

A

1006-7949(2011)03-0005-04

2010-05-07

国家自然科学基金资助项目(40901214);精密工程与工业测量国家测绘局重点实验室开放基金资助项目(PF2009-2)

徐秀川(1985-),男,硕士研究生.

[责任编辑刘文霞]