基于SLR的 GRACE卫星定轨中重力场模型对轨道精度的影响
徐克红,王 赫,王永富
(1.辽宁省国土资源厅信息中心,辽宁 沈阳 110032;2.沈阳金土科技有限公司,辽宁 沈阳 110032)
基于SLR的 GRACE卫星定轨中重力场模型对轨道精度的影响
徐克红1,王 赫2,王永富2
(1.辽宁省国土资源厅信息中心,辽宁 沈阳 110032;2.沈阳金土科技有限公司,辽宁 沈阳 110032)
以 GRACE卫星为例,分析比较利用SLR观测资料进行卫星定轨时,采用不同重力场模型对 GRACE卫星定轨精度的影响;以及重力场截断阶引起的积分轨道差异;同时,将定轨结果与采用 GPS确定的定轨结果进行比较,分析与 GPS定轨结果的差异。实验证明,重力场模型选择 GGM 02C的定轨结果优于选择JGM-3的定轨结果,基于SLR的定轨结果与采用 GPS确定的定轨结果差异量级为米级。
SLR;GRACE;重力场模型;CASMORD
航天技术的迅速发展,使卫星的应用越来越广泛,近二十年来,低轨卫星由于特殊的应用和科研的需要得到迅速的发展,在很多方面发挥了重大的作用。低轨卫星的应用与科学实验,对轨道精度提出很高的要求。然而,由于低轨卫星的轨道较低,受到地球重力场的扰动以及大气阻力等摄动力影响较大,故选择不同的摄动力模型会对卫星的定轨精度产生不同程度的影响。
在以 GPS观测作为测地卫星的主要跟踪技术来支持精密轨道确定的当代,卫星激光测距(SLR)由于能够提供所有用于跟踪卫星的测量方法中最精确的和最直接的轨道观测量,因此,在轨道的确定过程中,SLR观测仍然具有重要的价值。
1 国内外对 GRACE卫星的研究进展
GRACE卫星自发射以来,国内外学者对其轨道确定进行了大量的研究,定轨精度也在不断提高。例如,国外学者 M iloslawa Rutkow ska和Janusz Zielinski利用全球观测网获得的SLR观测资料,得到 GRACE卫星的定轨精度为0.5 m,国内学者韩健在定轨中增加了星载加速度计数据使定轨精度得到提高,还有杨龙、董绪荣利用 GPS非差观测值,及星载加速度计测量值,对 GRACE卫星进行精密定轨,得到 ITRF2000参考系下三轴精度优于18 cm。这些结果都为今后GRACE卫星的定轨精度提供了基础和比较。
2 数据的处理与分析
2.1 数据处理
使用的原始观测数据是从全球人卫激光站获得的标准点数据,标准点数据格式包括标准点数据记录部分(以99999为标识)和样本工程数据记录部分(以88888为标识),在此所用的数据只包括标准点数据记录部分。由于对定轨弧段长度的选择不同,从而将数据连接,之后对数据进行格式转换,转换为全频率数据格式,再对其进行排序,从而得到定轨过程中所使用的观测数据文件。
2.2 定轨结果的精度分析
定轨精度的评定是在一定的假设条件下,通过对实测数据的拟合程度,通过多种定轨结果的相互比较,给出的一种综合评定结果。实际工作中常用内符合精度和外符合精度两种形式来检核定轨精度。
定轨结果的内符合精度使用轨道拟合后残差的均方根误差(RM S)和估计协方差矩阵P表示。内符合精度取决于定轨方法的精密程度、测量数据的精度、定轨数据时间弧段的长短、定轨过程中求解的未知的数目、以及定轨过程中对测量数据的使用情况等诸多因素。
定轨结果的外符合精度是与使用其他方法获得的轨道确定结果相比,通常要比被鉴定的轨道确定结果的精度高或相当,才能得出比较符合实际情况的评定精度。
3 定轨软件
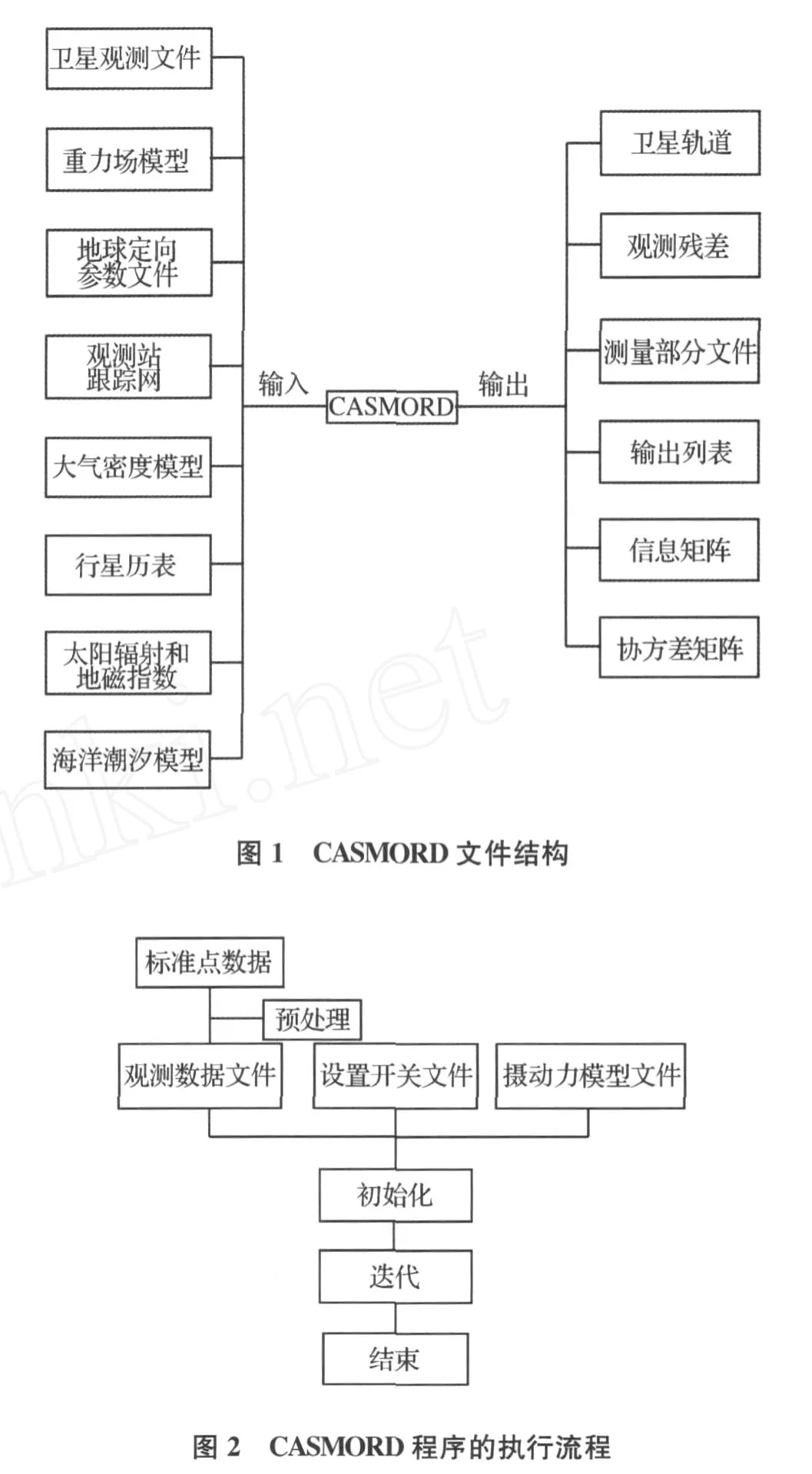
本文在进行定轨过程使用了CASMORD软件,它是由U TOPIA软件演化而来的,该程序的文件结构如图1所示。
CASMORD程序的执行流程如图2所示。
4 实验与分析
卫星围绕地球运动,地球的球心引力和地球的非球形摄动是维持和影响卫星运动的主要因素。本文基于地球重力场模型JGM-3和 GGM 02C,分别取70阶,50阶、70阶和90阶进行卫星轨道计算,探讨重力场模型对卫星轨道的影响大小。
描述地球重力场的标准形式是地球引力位的球谐函数展开式,建立重力场模型就是求解这一球谐展开式的系数,这些球谐系数称为位系数。
4.1 联合重力场JGM模型序列和 GGM 02C模型
JGM模型序列是由NASA/GSFC、TEXAS大学宇航研究中心和法国宇航研究中心(CNES)联合推算的,称为联合重力场模型(Joint Gravity Model)。这一模型是供T/P卫星精密定轨之用。其中,JGM-3是在JGM-2的基础上纳入T/P卫星的GPS跟踪数据得出的。
U TCSR于2004-10-29日公布了 GRACE地球重力场模型 GGM 02,其包含 GGM 02S和 GGM 02C两个模型。其中,GGM 02S模型是由 GRACE数据独立解算得到的,未加入任何其它的重力信息。随后,GGM 02S重力场模型同地面重力测量数据进行联合解算得到了重力场模型GGM 02C。
4.2 比较JGM-3和 GGM 02C模型对定轨精度的影响
为了讨论重力场模型对轨道精度的影响大小,重力场模型分别选JGM-3(70×70阶)和 GGM 02C模型(70×70阶)进行卫星定轨,研究不同重力场模型对GRACEA和GRACEB两个卫星轨道的影响。
所考虑的摄动力及所选用的模型为:地球非球形摄动、大气阻力(DTM 模型)、固体潮摄动(Wahr1980模型)、海潮摄动(U TCSR模型,该模型是以 Topex和Schw iderski模型为基础的)、太阳辐射压摄动、地球辐射压摄动、相对论摄动、N体摄动(考虑了太阳、月球、水星、金星、火星的摄动)和经验RTN摄动。
测量模型为:瞬时激光测距模型、卫星坐标系中3个方向的质心改正、对观测量进行对流层大气折光改正、相对论效应改正。观测站跟踪网的坐标框架为ITRF97,共154个观测台站。
估计参数为:大气阻力参数 Cd,太阳辐射压系数η,卫星的径向、横向和法向加速度。估计时间为:大气阻力系数每6 h估计一次,且给出先验值2.2;太阳辐射压系数每12 h估计一次;卫星径向、横向、法向的加速度每3.6 h估计一次。
采用以上模型,在重力场模型分别选JGM-3和GGM 02C,阶数均为70×70的情况下,对 GRACEA和 GRACEB进行定轨,结果比较如图3所示。
由图3可知,采用不同的重力场模型,对卫星轨道的影响还是很大的,GRACEB卫星反映更为明显。同时,从 X、Y、Z 3个方向上,Z方向所反映的差异最大。因此,在轨道确定中,重力场模型的选择对定轨结果有很大的影响,应通过实验的比较分析,选定恰当的重力场模型。

图3 采用两种重力场模型的积分轨道差异
对以上的比较分别从 X、Y、Z 3个方向的最小值、最大值、平均值、标准差几个方面进行统计,如表1所示。

表1 统计JGM-3和GGM 02C两种模型的积分轨道差异
由表1可见,从最小值和最大值来看两种模型的差异,GRACEA的差值跨度比 GRACEB要大很多,与图中所反映的一致。从平均值来看两模型的差异,GRACEA三方向平均值分别为0.70 m、0.41cm、3.08 m,GRACEB分别 为 0.90 m、3.39 m、6.58 m,GRACEA比 GRACEB要小的多。从标准差来看两模型的差异,GRACEA比 GRACEB小的多,反映了 GRACEA卫星上两模型的差异相对集中,GRACEB卫星上则比较分散,这也与图中所示相一致。
4.3 重力场模型截断阶引起的积分轨道差异
为了讨论重力场模型的不同阶次对轨道精度的影响大小,在此分别取重力场模型 GGM 02C的50阶、70阶和90阶的情况对 GRACEA和 GRACEB进行定轨,研究重力场模型截断阶引起的轨道差异。
其他摄动力的模型选择、测量模型、估计参数的情况,与4.2相同。分别从 GRACEA、GRACEB进行比较,如图4、图5、图6所示。

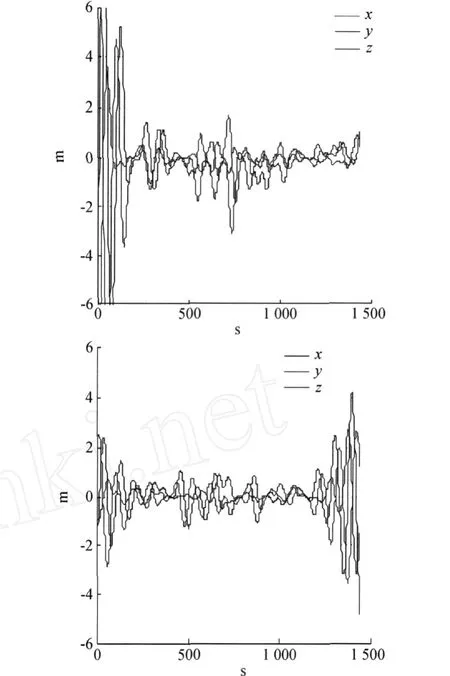
图6 重力场模型截断阶引起的积分轨道差异(50与90)
由图4、图5、图6中可见,重力场模型分别取70阶与90阶的情况相比,轨道的差异最小;而取50阶与90阶的情况相比,轨道差异要大的多。由此可见,轨道差异随着取得阶数的增多,之间的差异减小,在进行轨道确定的过程中,应尽量取较高的阶次。
4.4 重力场模型选JGM-3模型与采用CPS确定的定轨结果进行比较
重力场模型选JGM-3模型(70×70阶),其他模型选择情况与4.2节相同,在此基础上对 GRACEA与 GRACEB进行定轨,将所得轨道结果与采用 GPS的轨道结果相比较,如图7所示。
由图7可见,此种情况下的轨道与采用 GPS所得的轨道相比,X、Y、Z方向上的差异均很大,即此种情况下外符合精度不好。对二者的轨道差异进行统计,如表2、表3所示。
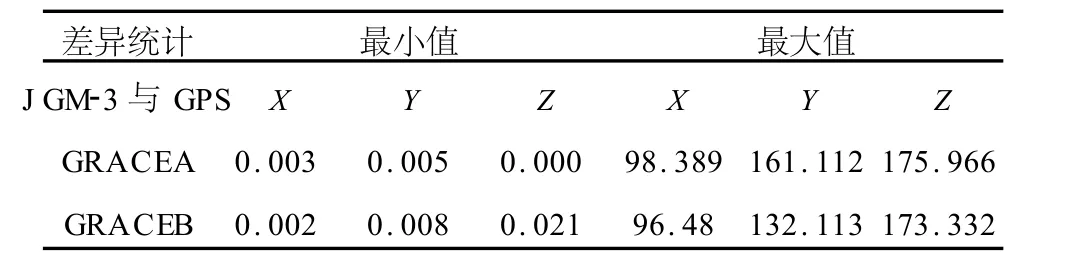
表2 统计重力场模型选JGM-3与GPS结果的轨道差(最小值和最大值)
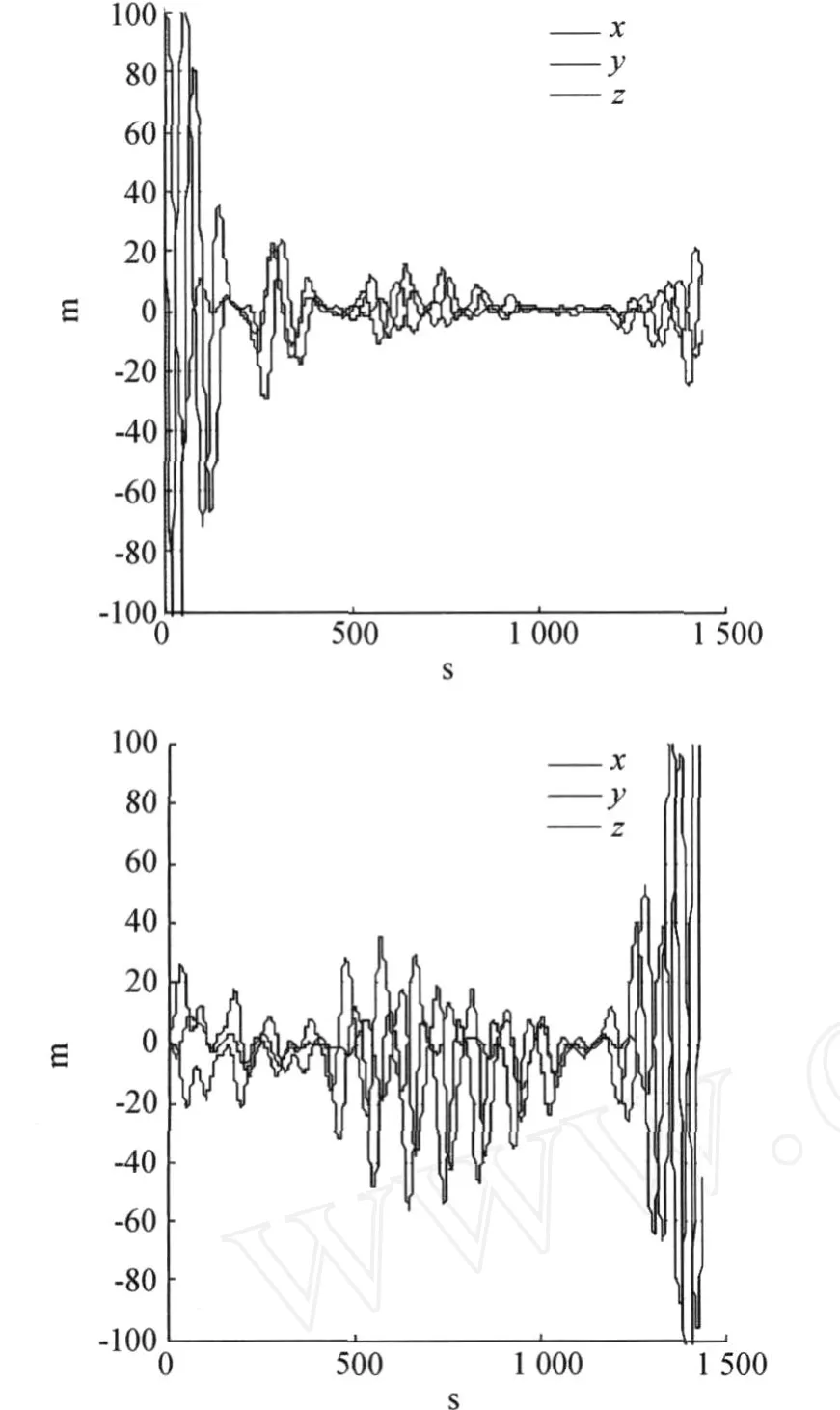
图7 重力场模型选JGM-3与GPS结果的轨道差异

表3 统计重力场模型选JGM-3与 GPS结果的轨道差(平均值和标准差)
4.5 重力场模型选 GGM 02C模型与采用CPS确定的定轨结果进行比较
重力场模型选 GGM 02C模型(90×90阶),其它模型选择情况与 4.2节相同,在此基础上对GRACEA与 GRACEB进行定轨,将所得轨道结果与采用 GPS的轨道结果相比较,如图8所示。
由图8可见,该情况下得到的轨道,与 GPS的轨道相比存在一定差异,差异的量级为米级,同时与图7相比,该模型下的差异比选JGM-3模型的差异要小的多。另外,对图8的轨道差异进行统计,如表4、表5所示。

图8 重力场模型选GGM 02C与 GPS结果的轨道差异

表4 统计重力场选 GGM 02C与 GPS结果的轨道差异(最小值和最大值)

表5 统计重力场选 GGM 02C与 GPS结果的轨道差异(平均值和标准差)
由表 4与表 5可见,最大值:GRACEB比GRACEA要大的多,与图 8所示相同;平均值:GRACEA与 GRACEB的差异均为几十个厘米,相比而言,GRACEA的差异较小;标准差:GRACEA的值较小,反映了差异较集中,与图8中所示相一致。
5 结 论
本文利用2002-05-08日的SLR观测资料,分别选用不同的重力场模型对 GRACEA、GRACEB进行定轨,并对得到的定轨结果进行比较,分析不同模型对定轨的影响差异;同时对重力场的不同阶次进行了实验,分析重力场截断阶所引起的轨道差异;最后,将定轨结果与采用 GPS确定的定轨结果进行比较,分析与GPS定轨结果的差异。通过比较分析,得出以下结论:
1)在其它摄动力模型一致的情况下,重力场选GGM 02C模型的GRACE卫星定轨结果与选JGM-3模型的定轨结果差异明显,且选择 GGM 02C模型的定轨精度优于JGM-3模型的定轨精度;重力场模型相同的情况下,随着阶次的增多,定轨结果的差异也在减小;这些将为卫星定轨中重力场模型的选择、模型中阶次的选择提供参考。
2)基于SLR的定轨结果与采用 GPS确定的定轨结果差异较明显,量级为米级,这是由于SLR技术观测资料少,且不能进行连续观测,所以对低轨卫星的定轨还存在局限性。但由于该观测技术可提供最精确、最直接的轨道观测量,因此,可将SLR观测作为辅助手段,考虑与 GPS等测轨技术相结合进行联合定轨。
[1]ROBERT,C.E.An Analytic Model for Upper A tmosphere Densities Based Upon Jacchia’s 1970 Models[J].Celestial Meah.1971(4):368-377.
[2]李济生.人造卫星精密轨道确定[M].北京:解放军出版社,1995.
[3]刘红新.CHAM P卫星定轨方法研究[D].上海:同济大学,2006.
[4]秦显平.基于SLR技术的卫星精密定轨[D].郑州:信息工程大学,2003.
[5]荀巍,乔书波,易维勇.中低轨卫星定轨精度分析[J].解放军测绘学院学报,1999,16(2):93-97.
[6]杨龙,董绪荣.利用 GPS非差观测值的 GRACE卫星精密定轨[J].宇航学报,2006,27(3):373-378.
[7]冯初刚,朱元兰,张飞鹏.SLR资料的快速处理[J].测绘学报,2001,30(3):226-230.
[8]郭金来,赵齐乐,郭道玉.低轨卫星精密定轨中重力场模型误差的补偿[J].武汉大学学报:信息科学版,2006,31(4):293-296.
[9]韩健,杨龙,董绪荣.星载加速度计数据在卫星定轨中的应用[J].上海航天,2006(4):20-22.
[10]秦显平,杨元喜,焦文海,等.利用 SLR与伪距资料综合定轨[J].武汉大学学报:信息科学版,2003,28(6):745-748.
The study of the track accuracy effect by GRACE satellite orbit’s gravity field model based on the SLR
XU Ke-hong1,WANG He2,WANG Yong-fu2
(1.Liaoning Land Resource Department Info rmation Center,Shenyang 110032,China;2.Shenyang Jintu Tech Co.,L td.,Shenyang 110032,China)
The paper takes GRACE satellite as an examp le.Then,it analyzes the different effects on o rbit determination caused by differentmodels based on SLR observation of GRACE satellite,and the truncation order of the gravity field caused by differences in the integral rail.Finally,the paper compares the o rbit determination result of SLR w ith GPS.Experimental results show that the gravity field model selection GGM 02C orbit determination resultswere better than JGM-3 orbit determination results.SLR-based o rbit determination results determined using GPSorbit determination results for themeter-scale order of magnitude difference.
SLR;GRACE;gravity field model;CASMORD
P228
A
1006-7949(2011)03-0015-06
2010-04-15
徐克红(1982-),女,工程师.
[责任编辑刘文霞]

