航空重力测量中的厄特弗斯改正
田颜锋,刘晓刚,孙 文,朱 军
(1.信息工程大学 测绘学院,河南 郑州 450052;2.73603部队,江苏 南京 210049)
航空重力测量中的厄特弗斯改正
田颜锋1,2,刘晓刚1,孙 文1,朱 军2
(1.信息工程大学 测绘学院,河南 郑州 450052;2.73603部队,江苏 南京 210049)
为提高航空重力测量数据的处理精度,在分析厄特弗斯改正计算模型的基础上,研究飞机的速度误差、方位误差和位置误差对厄特弗斯改正的精度影响,进一步研究模型中平方项对滤波处理的影响。结果表明:速度误差是影响厄特弗斯改正精度的主要因素,另外,厄特弗斯改正不需要进行滤波处理。
航空重力测量;厄特弗斯改正;滤波处理;预滤波
重力是地球引力和地球自转产生的离心力的合力,航空重力测量时,航空重力仪除受到地球自转产生的离心力影响外,还受到飞机速度产生的附加离心力的影响,这种影响称为厄特弗斯改正。当飞行方向与地球自转方向一致时,重力仪所受到的离心力增大,测得的重力值比实际的重力值小,反之测得的重力值比实际的重力值大[1]。因此,分析厄特弗斯改正的形成原理并分析各观测量对其计算结果的精度影响,对于提高航空重力测量的精度具有重要意义[2-4]。
1 厄特弗斯改正的数学模型
厄特弗斯改正由匈牙利科学家R.Eötvös首先导出并于1919年在实验室得到验证[1]。它是由飞机的运动附加于重力仪而产生的,与飞机的位置、速度、方位角和航高有关。如图1所示,当航空重力仪在纬度为φ、大地高为 h的一点 P处静止不动时,所受到的离心力可以表达为[3,5]


图1 重力仪受力分析
式中:Rφ为纬度φ处的地球半径,ω为地球自转角速度,h为载体飞行高度,离心力投影到垂线方向为
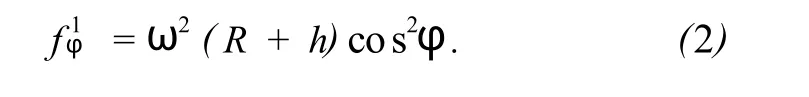
当航空重力仪随载体运动时,设航速为 v,ve和vn分别为速度的东向分量和北向分量,航向方位角是 A,如图2所示。则其相应的角速度分别为 ve/r、vn/Rφ,此时,离心力在引力方向上的投影为


图2 载体速度分解示意

2 厄特弗斯改正的精度分析
由式(4)可知,厄特弗斯改正主要受载体位置、速度和航向的影响。为便于讨论,采用球近似情况下的数学模型分析位置误差、速度误差和方位误差对厄特弗斯改正的计算精度影响。对式(5)取微分可得

接下来分析不同观测量对厄特弗斯改正的影响,取载体速度为220 km/h,地球半径R=6 378 137.0 m,自转角速度ω=0.000 072 921 15 rad/s。
2.1 速度误差的影响
图3显示了不同位置、不同航向时0.03 m/s的测速误差(目前 GPS的测速精度[6])对厄特弗斯改正的影响,从中可以看出,在赤道附近南北方向飞行时速度误差对厄特弗斯改正的影响达到最大,约为0.5×10-5m s-2。

图3 d v=0.03 m/s时厄特弗斯改正随φ和A的变化
2.2 方位误差的影响
从式(7)可知,在赤道附近方位误差对厄特弗斯改正的精度影响最大,表1显示了不同方位时方位误差对厄特弗斯改正的影响,可以看出,20″的方位误差在赤道时可引起0.08×10-5m s-2的厄特弗斯改正计算误差,因此,相对于速度误差而言,方位误差的测量影响可以忽略不计。

表1 方位误差对厄特弗斯改正的影响
2.3 位置误差的影响
从式(8)可知,测线方向为南北时位置误差对厄特弗斯改正的精度影响最大,表2显示了不同纬度时位置误差对厄特弗斯改正的影响,从中可以看出,20″的位置误差在赤道时可引起0.08×10-5m s-2的厄特弗斯改正误差,目前 GPS的定位精度优于米级,对应的定位误差小于1″,因此,位置误差的影响可以忽略不计。

表2 纬度误差对厄特弗斯改正的影响

综上所述,厄特弗斯改正的精度优于0.5×10-5m s-2。
3 滤波处理分析
实践中通常使用式(4)进行厄特弗斯改正的计算,试验采用 CGCS2000参考椭球新参数,某地航空重力测量时飞机航速约220 km/h,航高约500 m,运载平台为国产某航测机。计算得到的厄特弗斯改正如图4所示,由于航空重力测量中飞机飞行环境的影响,飞机的位置、速度、方位角数据中含有高频噪声,因此,需对其进行平滑或滤波处理。

图4 未经滤波的厄特弗斯改正
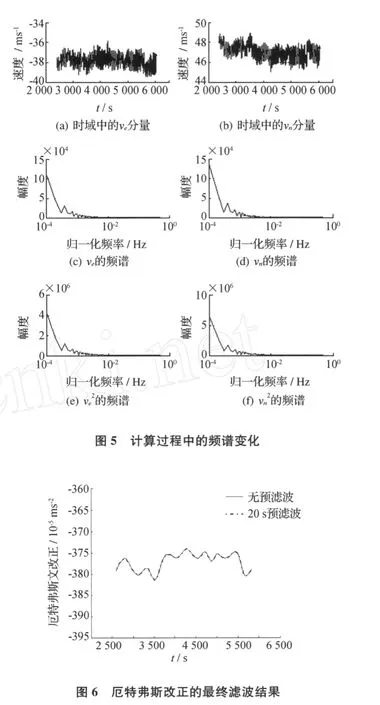
航空重力测量中各观测量的误差通常被认为是高斯白噪声,但是模型中的平方项会引起噪声的非线性变化,因此,需讨论平方项对最终滤波处理结果的影响。首先分析计算过程中的频谱变化,速度分量平方前后的频谱变化如图5所示。
从图5可以看出,厄特弗斯改正中的平方计算只改变了速度谱的幅度,并没有引起频谱成分的明显变化。图6显示了厄特弗斯改正的最终低通滤波结果,从中可以发现,没有预滤波的结果和原始数据经20 s预滤波后的最终滤波结果重合,因此,厄特弗斯改正不需要进行预滤波处理。
4 结束语
本文分析了飞机的速度误差、航向误差和位置误差对厄特弗斯改正精度的影响。目前 GPS动态定位的精度优于1 m,测速精度优于0.03 m s-1,在此前提下位置误差和航向误差对航空重力测量的影响可以忽略不计,速度误差成为影响厄特弗斯改正误差的主要因素,最大可达0.5×10-5m s-2。由于受飞行条件的限制,计算得到的厄特弗斯改正需经过低通滤波处理,对计算过程中的频谱变化追踪表明,模型中的平方项未引起频谱成分变化,因此,厄特弗斯改正不需要进行预滤波处理,实测数据处理也验证了这一结论。
[1]陆仲连.地球重力场理论与方法[M].北京,解放军出版社,1996:54-56.
[2]孙中苗.航空重力测量理论、方法和应用研究[D].郑州:信息工程大学,2004.
[3]赵立业,李宏生,周百令,等.高精度海洋重力测量中厄特弗斯改正误差分析[J].中国惯性技术学报,2008,16(4):462-465.
[4]汪凤林,蔡体菁.速率方位惯性平台/计程仪/重力匹配组合导航系统仿真研究[J].中国惯性技术学报,2005,13(5):24-28.
[5]李姗姗,吴晓平.GA INS中重力传感器信息的扰动改正[J].测绘科学技术学报,2007,24(4):270-273.
[6]王丽红.航空矢量重力测量中载体矢量加速度的确定方法[D].郑州:信息工程大学,2008.
Eötvös correction of aerial gravity measurement
TIAN Yan-feng1,2,L IU Xiao-gang1,SUN Wen1,ZHU Jun2
(1.Institute of Surveying and Mapping,Info rmation Engineering University,Zhengzhou 450052,China;2.73603 Troop s,Nanjing 210049,China)
In order to imp rove the disposal p recision of the surveying data in aerial gravity measurement,the influence of the airplane’s velocity error,orientation error and position error to the p recision of Eötvös correction are studied based on the analysisof the computationalmodel of Eötvös co rrection,and the influence of the square item s in themodel is further studied.The results show that the velocity erro r is themain facto r in the influence of the Eötvös co rrection p recision,and the Eötvös co rrection has no use fo r filtering p rocessing.
aerial gravity measurement;Eötvös correction;filtering p rocessing;p re-filter
P223;U 666.1
A
1006-7949(2011)03-0009-03
2010-04-09
国家自然科学基金资助项目(40774031);卫星导航与定位教育部重点实验室(B类)开放基金资助项目(GRC-2009010)
田颜锋(1981-),男,助理工程师,硕士研究生.
[责任编辑刘文霞]

