若干重要数论问题的证明

沈卫国

若干重要数论问题的证明

沈卫国

（西北工业大学信息智能与逻辑研究所，陕西省西安市 710072）

通常认为，若干重要数论问题是不能用初等数论的方法解决的。但这一结论本身就未加证明。文章尝试用初等数论的方法，对若干这样的问题进行证明，其过程简单、明确。结论具有易判性。

角谷猜想；3n＋1猜想；冰雹猜想；乌拉姆猜想；强哥德巴赫猜想；黎曼猜想；证明；初等数论

一、角谷猜想（冰雹猜想、3n＋1猜想、哈塞猜想、乌拉姆猜想、叙拉谷猜想）

角谷猜想为：任何奇数乘以3，再加1（3n＋1，n为任何奇数），得到一个偶数后，再不断除以2，直到得到一个奇数。然后再重复上述操作，最后终会得到1。以下寻求这个猜想的证明。

引理1：3n＋1，n为奇数，所得偶数间隔必为6的倍数。

证明：极其明显的，作为奇数的n的间隔为2的倍数。乘3，自然得6的倍数；每次均加1，间隔不变。即：n＝1时，为4；n＝3时，为10；n＝5时，为16；……………等等。当然，这些数并不全是偶数。

引理2：由角谷猜想的运算步骤，除了n＝1的情况，不可能出现循环。即由任一奇数n（n≠1）出发，经反复操作，又能得到该奇数n的情况不可能出现。

证明：完成一次角谷猜想的操作结果：

完成两次角谷猜想的操作结果为：

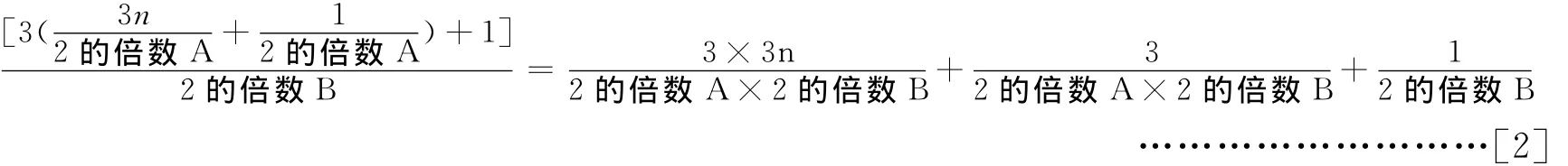
完成第三次角谷猜想操作的结果为：

我们还可以不断做下去。

如果在某一步后，正如角谷猜想所预言的，都会得到1，则整个式子应等于1。以［3］式为例（假设整个操作以3次结束），令其等于1，则可得到：

可以看到［4］式右边分子、分母都是奇数，因此等式右边完全可以得到整数，此式完全有可能成立。

另一方面，如果按角谷猜想的运算步骤，若干步后最终得到原设奇数，即运算是循环的，则［3］式右边必等于原设初始奇数n，则可得到：

可以看到，尽管［5］式右边分子、分母都为奇数，但其为负数，而n必须为正数。因此，此式不可能被满足（也就是［3］式右边不可能等于n），于是角谷猜想的运算在n≠1时不可能出现循环，得证。

引理3：对偶数而言，如果其形式为奇数×2，即只有一个2因子，则相邻两个奇数所产生的两个偶数间隔为4。如6，10，14，………等等，同理，形式为奇数×4的，间隔为8。如12，20，28，…………等等。同理，奇数×8的，间隔为16；奇数×16的，间隔为32；………………，依次类推。其证明类似引理1，从略。直观的，参见表1。表中每一偶数的下角标的数字，为该偶数中2因子的个数。特别应注意，只有2因子的偶数（因子1自然不算）2，4，8，16，32，64，128，……………等等，其相邻两数的间隔是以指数级别越来越大的，即2n，n＝1，2，3，4，…………。由引理3（同时参见表1）可以理解，只含一个2因子的偶数，占全部自然数的1／4，也就是占全部偶数的1／2。而有两个以上2因子（即4因子以上）的偶数，占到全部偶数的另外1／2；其中只是两个2因子（即4因子）的占整个偶数的1／4；三个2因子以上的，占到整个偶数的另外1／4；同理，只是三个2因子（即8因子）的，占到整个偶数的1／8；四个2因子以上的，占到另外的1／8；…………，其它依次类推。

表1

从表1我们还可看到，满足角谷猜想3n＋1操作所得到的偶数，由于间隔为6，因此，只能为：42（n＝1时），101，164，221，282，341，403，461，522，581，646，701，762，821，883，941，1002，1061，1124，1181，………………等偶数，其中只有一个2因子的，仍占这一偶数子集的1／2；有两个2因子的，占1／4；有三个2因子的，占1／8；……………。这可看成是引理4，其证明很简单：间隔6中有奇数因子3，因此与纯含2因子的间隔4，8，16，32，…………等，不可公度。因此所取到的含不同数量的2因子的偶数占所取偶数总数的比率，仍与原先一样。

可以看出，如果要通过角谷猜想规定的运算步骤最终达到1（即角谷猜想如成立），须先得到只有2因子的那些偶数（或只有1这一个奇因子），我们看到，在经过3n＋1（n为任意奇数）的运算后，是可以得到4，16，64，256，……………等等的（当然没有8，32，128，……………等等）。反之，如果角谷猜想不成立，这些无奇因子的偶数必然不会通过某个或某些奇数n的3n＝1运算得到。而由我们前面证明的引理3知道，角谷猜想的运算过程不会导致循环。同时在任一给定范围内，满足3n＋1运算的偶数有限，因此，要想满足上述条件，只有这一或这些奇数每一次进行角谷猜想运算的结果，总趋势是所得数（无论偶数还是奇数）逐渐变大的，否则早晚会达到4，16，64，256，…………之类只包含2因子的（自然不算1“因子”本身）偶数，也就是达到1。换言之，要保证从某或某些奇数开始的这种运算的结果，必须永远“遗漏”4，16，64，256，…………这样的偶数才有可能。

由引理3及表1可知，某类数的间隔越大，在总数中所占比率相应越小；反之则越大。而比率越大，无论随机取数还是顺序取数，取到的都相应多；反之则少。而且比率是与间隔相当的。同理，又由引理4，如果间隔为6地取数，在取数多时与随机取数相似；或在取数少时看作顺序取数，于是，取到的偶数类型所占的比率，是与其在全部偶数集中的比率相当的。如果同时考虑角谷猜想的运算步骤的约束条件，同时它的运算得数如与随机取数无异，则经若干次运算操作后，得数必然减小而非增大，于是不满足角谷猜想不成立的必要条件。这里我们有近似公式：

而K＝2，4，8，16，……………2p，……………。其中，p＝1，2，3，4，………………。同时，K≤n。

［6］式反映我们进行角谷猜想所要求的n次运算时，所最终得到的数的上限（最大可能数）与最初选择的那个奇数的比率。如果我们将n＝16代入，也就是假设有一个角谷猜想的运算进行了16次，则有＝25.628905×0.3164062×0.140625×0.1875×0.09375≈0.0200526

可见，在n足够大时，经过若干次角谷猜想的运算，所得数只能减小。因此不满足角谷猜想不成立的所得数必须增大的必要条件。当然，以上结果的前提是：角谷猜想的运算结果是类随机的。它不会在无穷个运算次数中都永远得不到某些特定的数，特别是仅以2作为因子的数。此点仍需证明。

我们知道，在角谷猜想的运算过程中如只除一次2即可完成（重新得到一奇数），也就是3n＋1运算后所得偶数只含一个2因子，则经过一次运算后，所得新的奇数是大于原设奇数的。因为

在n足够大时新得奇数约等于1.5倍原设奇数。如这运算可连续进行两次，则约为1.5×1.5＝2.25倍。依次类推，所得新的奇数是不断增大的。而如果3n＋1运算后所得偶数包含两个2因子（即4），则在运算后（n足够大时），所得新奇数约等于原设奇数的。依次类推，所得新奇数是不断减小的。而在一次3n＋1运算后得到只有一个2因子的偶数、下一次3n＋1得到有二个2因子（即4）的偶数的情况，则有，在n足够大时，约等于倍，只有微小增大。而其它情况，运算所得新奇数都将减小（读者可自行验证）。因此，要想在角谷猜想的运算中所得新奇数不断增大，必须重复以上二种运算，或以上二种运算不但存在，而且相对其它运算的比率足够多才行。但这一点在现实中不被满足，证明如下：

由某一奇数起始的某一具体角谷猜想运算过程，是角谷猜想运算过程可能得到的全部偶数集合的一个子集。因此也应该满足其全部性质。由引理4，从某个奇数开始的角谷猜想的具体运算过程如想刻意避开某些偶数，比如4，16，64，…………则必须满足公度性。但这一点同样已知不会被满足。因此经若干次角谷猜想规定的运算后必能达到上述那些偶数。得证。

通过上面的讨论、几个引理及其证明可知，角谷猜想必然成立。

二、强哥德巴赫猜想的证明

哥德巴赫猜想的表述早已为人所知，此处不再重复。但哥氏猜想并未就构成任一偶数的素数对的个数作任何陈述。换言之，任一偶数只要有一个素数对，哥氏猜想即成立。此文将证明，满足哥氏猜想的素数对存在下限，并且此下限随偶数N的增大而以固定规律（依赖于增大。这是一个比传统哥德巴赫猜想强的命题。为区别于传统意义的哥氏猜想，特称其为“强哥德巴赫猜想”。以下就此问题进行具体的分析。

由偶数的定义可知，任一偶数都是一个自然数与2的乘积。此时该自然数被认为是所给偶数的“中点”。其中又分为如下几种情况：

1、那个自然数（中点）是素数，如7、11、13、19等；

2、那个自然数（中点）是非素奇数，也就是包含素数因子的奇数，如9、15等；

3、那个自然数（中点）是包含素数因子的偶数，也就是同时包含偶数因子，如18、22等；

4、那个自然数（中点）是没有素数因子的偶数，也就是形如2n的数，其中n是任意自然数，如16、32、64等。

情况1，根本无需证明。两个该素数之和（或乘以2）。当然是偶数。如7＋7＝14。

其它几种情况，如将该偶数表为两个奇数之和，则必然是其中一个小于该偶数除以2后的中间数，另一个则大于该中间数，且该二奇数以此中间数为中心对称分布。比如偶数30，其中间数为30／2＝15，满足二奇数和为30的奇数对分别为13、17；11、19；………等等。它们每一组是以15为中心对称分布于二边的。毫无疑问，如果哥德巴赫猜想成立，则满足该猜想的素数对必也满足上述对称条件。下面先证明一个引理。

引理1：某素数的合数（指含该素数因子的数。这里包括该素数自身），在删除了其它素数的合数后的集合中所占的比率（当然包括其它素数因子的该素数的合数），与其全集在自然数中的比率一样，不变。

证明：设有某素数N，其合数（所有含其为因子之数）在自然数中的比率为1／N。在自然数中删去素数P（P≠N）的所有合数，即在自然数中删去了1／P个数，其中也包括素数N的合数中的1／P个。此时N的合数的个数为自然数自然数自然数在自然数中删去素数P的全部合数的集合

即此时剩余的N的合数的个数仍占删去素数P的所有合数后的集合的1／N，得证。

比如，3的所有合数占全部自然数的1／3，同样其奇合数也占奇数集合的1／3。因为删去的偶数集合中也包括了1／3的3的合数。比如6，12，18，等等。又比如5的合数，在删去全部偶数集合及全部3的合数集合后，在此剩余集合中5的剩余合数集合仍占其1／5。其余类推。

对于前文第2、3种情况中，由于所给偶数的中点数包含素数因子，于是由该中点数向二边（增大与减小）方向对该素数因子对称。于是以此中点数为中心左右两边（大与小）相互对称的奇数所构成的奇数对，要么同时是该素数的合数，要么不是。于是，是该素数S的合数的奇数对为全部以所给偶数的中点数为中心的素数对总数的个；反之，不是该素数合数的奇数对占总数的个。而对于情况4及情况2、3中，如果以中间数为中心左右（大、小方向）对称的奇数对中所包含的素数因子并非我们上面所讨论的情况，则相对该中点对所论素数是非对称的，即所论奇数对不能在中点二边对称位置同时得到包含所论素数的合数，而是有先有后。于是，满足所论素数S的合数的奇数对为所论奇数对总数的个；反之，不是该素数合数的奇数对占总数的个。当然，上述结果没有述及所论 奇数对的总数不能被该素数S整除这一极其普通的情况。实际上，在此情况下，我们舍弃相除的余数，只保留整数，如果结论不变，将会有误差。但如果所论偶数足够大时，误差是极小的，而且随偶数的增大越来越小。现举例予以直观说明：如果所选偶数为30，则中点数为30／2＝15，这符合“情况2”，其为素数3的合数。分别对称地位列15两边（满足其和等于30）的奇数对为13、17；11、19；9、21；7、23；5、25；3、27。注意，奇数对1、29不被计入，因为1通常不被认为是有意义的素数。我们看到，满足要求的奇数对共有6个，可以被所论素数3整除（其中有素数3因子）的有两对，为9、21；3、27。2／6＝1／3，即为总奇数对6的三分之一。如果所论偶数为36，则中点数为36／2＝18，符合“情况3”，其两边对称的奇数对为17、19；15、21；13、23；11、25；9、27；7、29；5、31；3、33。共8对，8除以所论素数3得，不能被所论素数3整除，如果如前面所论的做法舍弃余数（即分数2／3），则得整数2，但有所论素数3因子的奇数对有15、21；9、27；3、33。共三对，有误差。但这种误差随着所选偶数的增大将越来越小，而且对下面的讨论没有任何影响。如果所选偶数为32，则中点数为16，其不是所论素数3的合数（同时符合“情况4”），于是应该是“满足所论素数S的合数的奇数对为所论奇数对总数的个，具体这里也就是2／3（因为这里的“所论素数S”为3），而不再是1／3了。在16两边对称的奇数对为15、17；13、19；11、21；9、23；7、25；5、27；3、29。共7对。7乘以2／3，舍弃余数（分数部分）后整数部分为4，我们看到，上述7对奇数对中含有素数3因子的为5对，分别是15、17；11、21；9、23；5、27；3、29。相对于4而言，有所误差。但如果所选偶数非常大，我们将会看到，这种误差对下面将要进行的讨论无任何影响。

对于所论素数大于3的情况，读者可自行验证。

引理2：有某素数A及整数N，当A2＞N时，从N以下的任何数不会是大于A的两个素数相乘的合数。

证明很容易。设B＞A，则A×B＞A2＞N，得证。

引理3：任何间隔为2×某素数的两个奇数间，当然有该素数个不同的奇数，但其中必有、且只有一个含有该素数的奇合数存在。

证明：如其不然，则起码应有一个间隔为2×某素数的两个奇数间，没有（或有多于1个）含该素数的奇合数存在。也就是说，必然存在两个相邻的奇数，它们分别与该素数的乘积之差，大于（或小于）间隔2×该素数。但我们知道，任何两个相邻的奇数间隔为2，而如此的两个相邻的奇数分别与所论该素数的乘积（也就是包含该素数的奇合数）之差，即为也只为2×该素数。所以总会有一个且只有一个满足条件的奇合数存在。引理3得证。

引理4：任何间隔为4×某素数的两个奇数间，其中必有、且只有两个含有该素数的奇合数存在。证明：由于它的间隔比引理3所述情况的大一倍，所容纳的合数自然也多一倍，也就是两个。

我们知道，由“中间数”向大小两边对称、同步地列出奇数对时，其间隔正是以4的倍数增加的。由引理4可知，每当我们列出“某素数个”这样的奇数对时，必在中间数的大小两边分别各有且只有一个含有该素数的奇合数。同时，当该“中间数”本身就是该素数的合数时（注意，当然不一定是奇合数，也可以是偶合数），在上述做法下，含该素数的奇合数是成对（可视为“同时”）出现的，其它情况则不同时，也就是“分别”先后出现，即不成对出现。

以下将在上述讨论的基础上，证明强哥德巴赫猜想。

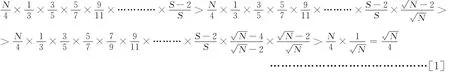
倒数第二步，为倒数第三步分子、分母上下相消所得。此式在N＞16时总被满足。特别当N→∞时，→!，即满足哥德巴赫猜想偶数N的素数对数不少于（由公式［1］）且随N趋于无穷而趋于无穷。这是一个比传统哥德巴赫猜想强的结论，因此，可称之为“强哥德巴赫猜想”。这里应该特别说明的是；上式中所有小于的素数，也被删去了（因其显然可以被自身整除）。但即使如此，哥德巴赫猜想也能被满足。如果算上由这些本不该删的素数可能构成的素数对，满足歌德巴赫猜想的素数对将更多。此外，也应该说明，偶数N内的奇数对为（取整）个，但1＋（N－1）类型的奇数对不能算。因为1不是一般的素数。通常将其排除在外，哥德巴赫猜想也不包含这种类型的素数对。所有公式［1］中的，实际应为－1。比如偶数32，中间数（中点）为16，算1＋15的奇数对共8个，不算的则为7个（有效的），但N足够大时，此误差几乎不用考虑。

前已述及，尽管公式［1］对证明哥德巴赫猜想已经足够，但由于将3、5、7、11等素数也记入了含素因子的合数中，因此对于确定素数对数目而言，并不精确。尽管这与传统哥德巴赫猜想已无关系，但给出一个更精确的素数对数目公式还是有意义的。这里我们提出更精确的公式：

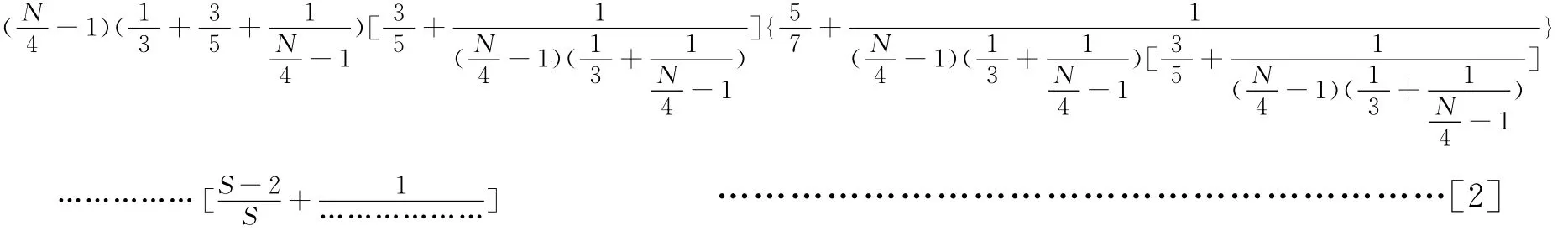
其中符号‖…………‖表示“取模”，即取整数部分。由于此细节对证明已无大碍，故可不予考虑。

至此，强哥德巴赫猜想得到证明。

为帮助读者理解，现举一个简单的例子予以说明。设所论偶数为92，其“中间数”为92÷2＝46，奇数对为46÷2＝23个。它们分别是：45、47；43、49；41、51；39、53；37、55；35、57；33、59；31、61；29、63；27、65；25、67；23、69；21、71；19、73；17、75；15、77；13、79；11、81；9、83；7、85；5、87；3、89；1、91。最后一对“1、91”当然无意义，可舍去。这些奇数对中不含素数3因子的奇数对约占23个的3分之1，它们分别是：43、49；37、55；31、61；25、67；19、73；13、79；7、85。共7对。其中不包含素数5因子的奇数对又约占7对里头的5分之3对，它们分别是43、49；31、61；19、73；13、79。共4对。其中不含素数7因子的奇数对又约占7分之5，共3对，分别是31、61；19、73；13、79。而大于素数7的素数为11，其平方为121，超过了所论偶数92，不予考虑了。实际上，上面3个奇数对，已经是素数对了。它显然大于强哥德巴赫猜想所要求的再取整。随着所论偶数（也可以说中间数）的增大，误差将越来越小，以致最终完全可以忽视。当然，特别应该提及的是，即使在所论偶数很小，误差存在的情况下，［1］、［2］两式也依然成立。

说明：笔者在得到本证明后，偶然发现胡桢（已去世）、唐国胜二先生以不同的方式得到与我几乎相同的结果，殊途同归。他们的论述究竟可否看作证明、或证明是否严密，是另一个问题。但无疑，这说明我们的结果都反映了素数的同一客观规律，值得重视。毕竟，三个人分别“独立地”错到一起去的可能性是很小的。同时，他们、特别是胡桢先生（据笔者目前的了解，他最早得到这一结果，尽管没有正式发表）的历史性贡献，应该得到充分的肯定。

三、黎曼猜想的间接证明

已知函数：

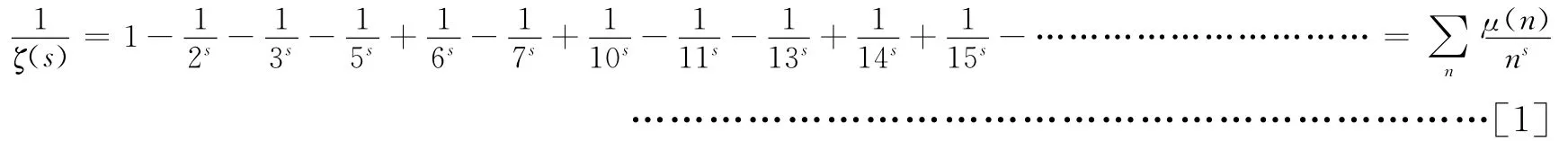
其定义域为自然数集。μ称为默比乌斯（AugustFerdinand M bius）函数。其定义为：

1、μ（1）＝1；

2、如果n有一个平方因子，那么μ（n）＝0；

3、如果n是一个素数，或者是奇数个不同素数的积，那么μ（n）＝－1；

4、如果n是偶数个不同素数的积，那么μ（n）＝1。

μ（n）的累加值称为麦尔滕函数M，即对某个数K，我们有：

M（K）＝μ（1）＋μ（2）＋μ（3）＋……………＋μ（K） …………………………［2］

M（K）围绕0不规则地在正、负数间来回摆动［1］。而下式

与黎曼猜想等价［1］。其中ε为任意小的数。O的定义为：如果对于足够大的自变量，函数A的大小绝不超过函数B的某个固定的倍数，那么函数A就是函数B的O［1］。

公式［3］实际是一个定理，它实际是说M函数的增长恰如一场掷币操作中的超出量。即一个无平方因子数要么有偶数个素因子，要么有奇数个素因子——这两种情况的概率各占如果能证明此结论成立，就等于间接证明了黎曼猜想［1］。下面，我们就着手进行证明。首先，我们有组合公式［2］：

由于可将麦尔滕函数看作奇数或偶数个素数的组合之代数和，因此只要n为奇数，由［4］式，可以确定它们相消为0。

如果偶数为＋，奇数为－，相应的二者数量又相等，当然可以相互消去，即其代数和为0。此关系在n→∞时仍成立。我们还有组合公式［2］：

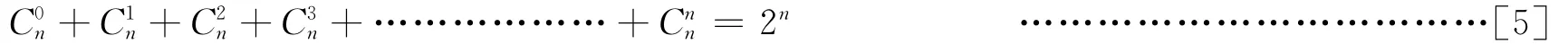
显然，［5］式只在左边各项为正时成立。当n为奇数时，如结合有正负的麦尔滕函数M，则上式左边的代数和为0。

此外，我们有另一个组合公式：

如果仅由［4］式，不同的正负数、也就是奇数个素数因子的数与偶数个素数因子的数是可以相消的，但那是多素因子的数与少素因子的数的相消，数的大小差距太大。而麦尔滕函数是依数轴大小顺序进行累加的（也就是相消），不是数轴上近端的数与远端的数相加（相消）。而［6］式则可避免此不严格的情况。如由［6］式，我们可有：

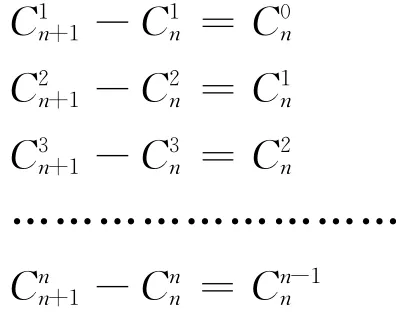
我们可以明显地看到，偶数因子与奇数因子在数量上相消的情况。而显然，如果这样的相消成立，则其出现几率必为50%︰50%，即黎曼猜想得证，尽管是间接的。

此外，另一黎曼猜想的间接证法如下：

用反证法。如果当素数项→∞时，偶数个素数相乘之项大于（或小于）奇数个素数相乘之项，则应有：

显然，如此就不可能再有Ck（偶数）n（奇数）＝Cn－k（奇数）n（奇数）即［4］式这样的关系存在，于是得证。

［1］约翰.德比希尔.素数之恋——黎曼和数学中最大的未解之谜［M］.上海：上海科技教育出版社，2008.

［2］郭建英等.概率统计［M］.北京：北京大学出版社，2005.

Proofs on a Number of Important Problems of Number Theory

SHEN Wei－guo

（Information Intelligence and Logic Institute in Northwestern Industrial University，Xi＇an，Shanxi Province，710072 China）

Generally speaking，a number of important problems of Number Theory cannot be solved by elementary Number Theory，which has not yet been proved.This article attempts to testify these problems in elementary Number Theory whose process is simple and clear.Besides，the conclusion features an easy judgement.

Jiaogu Guess；3n＋1 conjecture；hail conjecture；Ulam conjecture；strong Goldbach conjecture；the Riemann hypothesis；proof；elementary number theory

O156

A

1673－582X（2011）11－0100－08

2011－09－02

沈卫国（1950－），上海人，中国城镇供热协会区域供热杂志主编，被聘为西北工业大学信息智能与逻辑研究所研究员，主要研究科学理论、数学基础理论、热力学理论。