分解大整数为两个素因子乘积的析出算法
孙克泉
(南开社区学院计算机系,天津市 300100)
分解大整数为两个素因子乘积的析出算法
孙克泉
(南开社区学院计算机系,天津市 300100)
RSA的算法是基于数论中两个大素数乘积所得整数n和选取满足一定条件的整数e组成公开钥(e,n),RSA的安全性是依据大数整数n分解困难性的。根据RSA公钥加密体制的公开密钥n为两个素数乘积的特性,以及Euclid算法的特点,给出了一种分解n的算法—析出算法,并进行了算法的数学证明、算法设计和相关分析。同时,通过也证明了,在RSA密码体制中构造模n时,其素因子的倍数与n1/2距离过近是不安全的结论。
析出算法;RSA;Euclid算法;密码分析算法;算法数论
一、引言
RSA算法[1]是1978年由R.Rivest,A.Shamir和L.A dleman提出的一种用数论方法构造的非对称加密方法,它被认为是目前相当成熟、完善的公钥密码体制,并广泛地应用于密钥管理、数字签名等方面。
RSA的算法是基于数论中两个大素数乘积所得整数n和选取满足一定条件的整数e组成公开密钥(e,n),并选取特定私钥d组成私有密钥对(d,n)。对于RSA加密体制攻击是来自多方面的,同时对加密算法的密码分析是检验算法安全性的标志。因为在给定e和n和情况下,确定d的计算量至少等价于整数分解问题[2],所以RSA算法的安全性就是基于数论中大整数分解困难性的,一旦成功分解n,就很容易地得到了私钥d,也就破解了用RSA加密的内容。因此,在对RSA的密码分析方法中,大多数都集中在对公钥n的因式分解方法上,比如数域分解法、二次筛选法、椭圆曲线法和试除法等。
本文是利用RSA密钥加密中的公开钥n是两相大素数乘积的特性和Euclid算法的特点,给出了一种新的分解n的算法,这里称为析出算法(Analysis A lgorithm),并进行相关的理论证明和该算法设计,以及相关分析。同时得出在RSA密码体制中构造模n时,其素因子的倍数与n1/2距离过近是不安全的结论。
二、RSA算法的基本描述与安全性分析
1.RSA的公钥加密体制
由Rivest、Sham ir和A dleman开发的RSA方案利用了指数运算,明文以分组的方式被加密,其中每个分组是一个小于某一整数n的二进数,即分组的长度必须小于或等于log2n;实际上,分组长度k满足2k 发送者和接收者都必须知道整数n,发送者e,而只有接收者知道d的值。因此这是一个公钥加密算法,其中公开密钥 KU=(e,n),而私有密钥 KR=(d,n),RSA算法须满足以下要求: (1)对于所有m (2)对于m (3)给定e和n,求d是计算上不可行的。 2.RSA密钥的产生 (1)选两个保密的大素数p和q。 (2)计算n=pq,φ(n)=(p-1)(q-1),其中φ(n)是n的欧拉函数值。 (3) 选一整数 e,满足 1 (4)计算d,满足d·e≡1 modφ(n),即d是e在模φ(n)下的乘法逆元,因e与φ(n)互素,由模运算可知,它的乘法逆元一定存在。(5)以{e,n}为公开密钥,{d,n}为私有密钥。 3.RSA加密/解密运算 加密时首先将明文比特串分组,使得每个分组对应的十进制数小于n,即分组长度小于log2n。然后对每个明文分组m,作加密运算:memod n=c,其中c为明文m的e次幂与n的模运算。对密文分组的解密运算为:m=cdmod n,并且可以根据Euler定理证明解密的正确性[3]。 4.分解n的算法及RSA安全性分析 RSA的安全性是基于分解大整数的困难性假定,这种假定是因为至今还未能证明分解大整数n的问题。如果RSA的模数n被成功地分解为两相素数乘积n=pq,则立即获得φ(n)=(p-1)(q-1),从而能够确定e模φ(n)的乘法逆元 d,即d≡e-1modφ(n),因此攻击成功。如果给定 n,φ(n)等价于对n的分解[3];在给定e和 n的情况下,确定d的计算量至少等价于整数分解问题[2]。因此,只有分解n才能从c和e中计算出明文m。对n的因式分解方法中,通常的方法是采用数论中的因式分解方法。针对公钥n比较常用的因式分解方法有试除法、Fermat分解法、Pollard’s rho分解法、Pollard’s P-1分解法、Dixon分解法、连分数分解法、二次筛法、多多项式二次筛法、数域筛法和椭圆曲线法等。Pollard’s rho分解法、Pollard’s P-1分解法和椭圆曲线法都是概率分解的方法,都是要求被分解的模数有特殊的条件[4][5]。为了增强RSA的安全性,通常采用选择强素数的方法,以预防这类算法的攻击[6]。Fermat分解法、Dixon分解法、二次筛法、多多项式二次筛法、数域筛法等都是基于求同余式为x2≡y2(mod n)且x≠±y(mod n)所构成完全平方数x和y。只要求出x和y,即通过gcd(x+y,n)和gcd(x-y,n)达到分解n的目的。但求出这样的x和y通常是很困难的,必须构造有效的算法,利用一些数论技巧才能完成它。这些基于构造完全平方数的算法就是利用各用数论理论和技巧,如同余式、二次剩余、多项式等以及代数运算,通过比较复杂的算法构造,尽量缩减运算量,降低运算复杂度,以搞高分解n的效率。数域筛法被认为是当前最有效的算法[4][5]。 根据目前的研究,提高分解n的有效性和效率只是在这些算法的基础上,进行改进,如更好地构造多项式等[7],或给出分解特殊形式的n的方法[8],以提高分解效率。因此,当n的二进制位数在1024位以上时被认为是安全的。 本文根据n为两个素因子乘积的特性,以及求最大公约数的 Euclid算法,给出一种新的分解n的算法,不妨将它叫做析出算法。下面就给出该算法的相关定理及证明、算法设计,以及相关分析。 定义1设a,b为任意整数,如果存在整数c,使得a=bc,则称a是b的倍数,b是a的因数或约数,即a被 b整除,或 b整除a,记为 b|a。 定义2能够整除a,b,…l的每一个整数叫做它们的公约数,公约数中最大的一个叫做最大公约数 ,记作(a,b,…l)或 gcd(a,b,…l)。 定义3对于任意实数x,用[x]表示不超过x的最大整数。 定理1设n为两个素数乘积的正整数,n=pq,p和q为素数,且p 引理1(因子分解的唯一性):如果n=pq,p和q为素数,且p 引理2如果 n=pq,p和 q为素数,且p 证明:用反证法,如果p=[n1/2],由于 n=pq,所以 q=p=[n1/2],与p 如果p>[n1/2],由于 n1/2不是整数,则p>n1/2,得p2>n。由 q>p,得pq>n,与 n=pq矛盾。 因此p<[n1/2],同理可以证明q>[n1/2]。 定理1的证明:由p为素数,和引理1得知,必定存在一个正整数k(k≥1),使得 kp≤[n1/2]≤(k+1)p 引理3设a,b为正整数且b≤a,则唯一存在正整数d和r,使得 a=bd+r;0≤r 数d称为带余除法的不完全商数,数r称为b除a的余数。 特别地,如果r=0,则a=bd,由此得b和d是a的因数。 证明:假设还可以表示成:a=bd1+r1,0≤r1 引理4设a,b为正整数,且b≤a,不妨表示为a=bd+r。如果(a,b)=1,且m为a和r的公因子,则 m|(d,r);否则 m|(b,r)。 证明:如果 m=(a,b),即 m|a,m|b,由 a=bd+r和 m|bd+r,得 m|r,所以 m|(b,r)。因此有 m|(b,r)。设(a,b)=1,如果存在 m|r,m|a,则由a=bd+r,得 m|d,即 m|(d,r)。 定理2(Euclid算法(辗转相除法)) 设a,b为正整数,由于引理3,我们求得一串等式: 这串等式直到余数等0为止。而且 (b,r1)=(r1,r2)=(r2,r3)=…=(rn-1,rn)= rn. (证明略) 因为b,r1,r2,…,rn是是递减的正整数数列,不能包括多于b个的正整数,所以上述一串等式成立。 由引理4得(b,r1)=(r1,r2)=(r2,r3)=…=(rn-1,rn)= rn. 定理3设a,b为正整数且b≤a,表示为a=bd+r;0≤r 证明:因为d>b,所以在a=bd+r式中有0≤r 定理4设n为两个素数乘积的正整数,不妨设n=pq,p和q为素数,且p 证明:首先证明d>b>[n1/2]。假定 d<[n1/2],则 n=bd+r≥bd>[n1/2][n1/2]。因为[n1/2][n1/2] 由于引理3和引理4,有(n,b)= (b,r)或(n,d)= (d,r)。由引理2得知,p<[n1/2],q>[n1/2],以及n只有两个素因子p和q,因此,如果n与小于[n1/2]的数的最大公约数存在,则必为p。即(n,b)=p或(n,d)=p。 1.采用 Euclid算法分解n的方法 可以采用 Euclid算法分解n。由定理1,如果存在一个整数k≥1,使得kp≤[n1/2]≤(k+1)p,发现小于[n1/2]的正整数中含有n的素因子p的整数为p,2p,3p…kp =[[n1/2]/p]p。要从小于[n1/2]的数中筛选出含有n的素因子p,可以采用 Euclid算法进行。也就是说,依次取小[n1/2]的整数,然后用 Euclid算法求该数与的最大公约数,如果不存在,将该数减1,再重复使用 Euclid算法,直至求出n的素因子p,用具体设计方法是: (1)设一变量i的初始值为[n1/2] (2)根据定理2提供的 Euclid算法求n和i的最大公约数p(由定理4得知)。 (3)如果n与i互素,则进行i-1运算,然后返回(2),如果n与i存在公约数,必得到公约数p,进而求出n的另一个因子q。 2.Euclid算法分解n的方法分析 如果采用Euclid算法分解n,在设计一个程序运行的情况下,该方法的计算量与n的素因子p有关,进而与[[n1/2]/p]p有关。只有变量i递减到等于[[n1/2]/p]p时才能分解出n的素因子p,因为在大于[[n1/2]/p]p的数到[n1/2]都与是互素的。该方法的计算量取决于([n1/2]- [[n1/2]/p]p)3(最高一次辗转相除的执行次数)。它存在的的缺陷是: (1)对于求n与小于[n1/2]的数的公约数,一旦该数与n互素,则此次辗转相除的运算是徒劳的。由于在[n1/2]-[[n1/2]/p]p([[n1/2]/p]p除外)之间的数都与n互素,因此,在该区间上每次辗转相除都不能分解出素因子p。只有当分解的数为[[n1/2]/p]p时才能找到素数p。 (2)由定理1,kp≤[n1/2]≤(k+1)p(k≥1),即 k=[[n1/2]/p]。如果[n1/2]-[[n1/2]/p]p大于([[n1/2]/p]+1)p-[n1/2]时,也就是说,当大于[n1/2],而且距离[n1/2]与含有素因数p的数相对很近时,不能由此程序分解出该素数,从而降低了分解效率。 3.析出算法的原理、设计与分析 1)析出算法的设计 对于上述用Euclid算法分解n的方法,从效率上是可以进一步的改进的。为了弥补上述缺陷,构造出一种新算法,把它称之为析出法,算法设计如下: (1)设一变量i,它的初始值为[n1/2] (2)根据定理3和定理4,采用下列的相除法: 将n mod i的值赋给变量r,这样得到一个余数r。然后再求n mod r,依次类推,一直计算到预先设定的一个数s为止,s设定的依据是:被认为在小于s的整数中不可能存在素因子p。 实际上是求下列一串等式: (不妨设b=i) 在这里要对其中的rn是否小于s进行判断,一旦rn+1 (3)如果rn+1小于一个特定s且rn+1≠0,则进行i-1运算,然后返回(2),如果n与i存在公约数,必得到公约数p,进而求出n的另一个因子q。 2)析出算法的分析 该算法的原理是依据 Euclid算法效率较高的特点,主要是采用取余运算,相对减少了运算量。下面就该算法进行如下分析。 (1)由于是从小于或等于[n1/2]的数开始,依次递减操作,对于其中的任意一个整数b,根据引理4,都存在n=bd+r。由定理2,如果b≤[n1/2]中含有素因子p,则r中必包含素因子p,但是如果b不含有素因子p,也就是说n和b是互素的。如果按照 Euclid算法,最后只能得到gcd(n,b)=1。但是,此时r中并不一定不含有素因子p(通过实验验证是肯定的)。因此,该算法可以求r中含有n的素因子p。 (2)因为b是依次递减,所以d是递增的。虽然在每次运算中d的递增可能不是1,但很明显,在运算中,与上一次相比,如果d不是增1,是由于该数除n的余数大于[n1/2],经测试该算法仍能找到大于[n1/2]且与之最近的含素因子p的数,进而求得p。因此,该算法在计算了n=bd+r式中小于或等于[n1/2]的数b可能存在素因子p的同时,也计算大于[n1/2]商数d与r可能存在素因子的问题(由定理3)。 (3)关于算法中给定一个假定的数s,是为了减少算法中第2步的运算量,这个数的确定是根据RSA密码体制中,n取较大素因子的情况。例如,假设n的两个素因子为相同位数,且十进制位数为k,则s确定为10k-1。因为当小于s的所有整数不可能存在n的素因子。 (4)从概率角度分析,由于每次运算所得的余数r大部分是不同的,很可能在其中的某个余数中存在n的素因子。因此,该法存在求出n的素因子的随机性。 (5)为了增加求出n的素因子概率和提高分解速度,在算法中可以采用在一定范围内随机抽取小于[n1/2]的数进行第2步的运算。或采用多台机器分布运算的方法。 (6)由定理3,该算法的单一程序的最大运算量这min([n1/2]-[[n1/2]/p]p,([[n1/2]/p]+1)p-[n1/2])3(算法第2步的最大运算量)。 (7)不难看出,如果在[n1/2]附近存在含有n的素因子的数,那么,采用该算法会很快得到n的素因子,进而求出RSA加密的明文。因此,该算法能很容易分离出与[n1/2]较近的含有n的素因子的数,进行破解RSA的密钥;也就是说,如果n的素因子的倍数与n1/2距离较近时,RSA密钥体制是不安全的。 (8)虽然,大数取余的算法效率不是很高,但在还可以进一步改进该算法的设计方法,具体的算法设计的改进有待进一步研究。 (9)以上结果,在计算机上对小于64位的n进行了有效验证。 本文构造了RSA密码体制中分解公钥n的析出算法。它是通过改进Euclid算法,创造出的一种新算法。该算法利用了Euclid算法中求最大公约数效率高的特点,并充分利用了n是两个素数乘积的特性,试图提高分解n的效率,证明了如果一个数在n1/2附近含有n的素因子,使用该算法能比较容易地析出这个数所包含的n的素因子。由此也得出了一个结论:在RSA密码体制中构造模n时,其素因子的倍数与n1/2距离过近是不安全的。今后,对于该算法的计算方式,以及大数模n的分解还需进一步的研究。 研究背景: 依据对于算法数论和信息安全中RSA公钥体制中研究。尽量查找目前资料中所能查到的各种算法,并对其进行分析研究。在此基础上提出一种新的密码分析算法-析出算法,它是根据公钥n是两个素乘积的特性,在对Euclid算法的改进后得出一种新算法,它从理论上不同于其它算法。并给出了该算法的相关数学证明、算法设计和算法分析。 [1]L Rivest,A Shamir,L Adleman.A Method for Obtaining Digital Signatures and Public Key Cryp tosystems[J].Communications of the ACM,1978,21(2):120-126. [2]Ribenboin,P.The New Book of Prime Number Reco rds.New York:Sp ringer-Verlag,1996. [3]Kslidki,B.;and Robshaw;M.“The secure Use of RSA”Cryp toBytes,Autumn 1995. R L Rivest,A Shamir,L Adleman,“On Digital Signatures and Public Key Cryp tosystems”,Communications of the ACM,vol 21 no 2,pp120-126,Feb 1978. [4]颜松远,杨思熳等译.计算数论[M].第2版.北京:清华大学出版社,2008. [5]董青,吴楠.整数质因子分解算法新进展与传统密码学面临的挑战[J].计算机科学,2008,(08). [6]谢建全,阳春华.RSA算法中几种可能泄密的参数选择[J].计算机工程,2006,(16). [7]裴定一,祝跃飞.算法数论[M].北京:科学出版社,2002. [8]张鹏,李超.数域筛法分解re±s型大整数时多项式的选取[J].计算机应用与软件,2009,(04). [9]N,M.维诺格拉陀夫.数论基础.北京:高等教育出版社,1956. The Separation A lgorithm of D ividing Large Integer into Tw o Prim e D ivisor Product SUN Ke-quan RSA calculation is based on tw o divisors p roduct n and 1,w hich forms the conditional public key(e,n).The safety of RSA depends on the difficulty of dividing the large integer n.Accord2 ing to the characteristic of public key RSA and Euclid Calculations,this essay p resents a decomposing n’s calculation--Separation Algorithm,and undergoesmathematical p roof,design and analysis.At the same time,during the design of module n,it p roves unsafe if the integer multip le is too close to n1/2. separation algorithm;RSA;Euclid Calculations;code analytical calculation;Theo2 retic Algorithms TP309.7 A 1673-582X(2011)08-0037-06 2010-11-10 孙克泉(1961-),男,天津武清人,南开社区学院教师,硕士,副教授,CCF高级会员,主要研究领域为计算机应用,信息安全。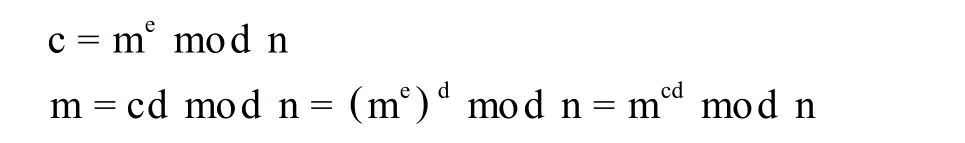
三、析出算法的相关定理

四、析出算法原理与分析

五、总结
(N ankai Comm unity College,Tianjin 300100 China)

