长寿风险、养老金体制与资本积累

胡仕强 ,许谨良

(上海财经大学 金融学院,上海 200433)

一、引 言

人口变化与经济增长之间的关系始终是经济学家和各国政府关注的话题,特别是人口老龄化的加速更凸显了此研究的紧迫性。众所周知,老龄化的两个微观基础是生育率的下降和预期寿命的延长,这两者产生的直接结果为劳动人口的增长比率低于消费人口的增长比率,从而导致人口红利的消失和人口窗口期的关闭。然而经济学常识告诉我们,低生育率(子女减少)和长寿本身又可成为改变人们消费储蓄模式的强大动因。根据莫迪利安(1954)的生命周期消费理论,个人在其生命周期内的消费—储蓄行为可以划分为工作期的储蓄和退休期的反储蓄两大阶段,工作期的收入等于整个生命周期的消费,如果生命周期延长而工作期没有相应延长,则工作期的储蓄积累就不足以支付退休期的消费,从而产生养老资源不足的风险,这就会促使人们增加资本积累以应对漫长的退休生活。而资本积累是经济增长的重要源泉,随之而来的资本深化必然会使人均产出快速增长,进而影响利率、工资、储蓄和消费等一系列宏观变量,人们称此为第二人口红利。因此,对人口结构变化与资本积累之间关系的研究具有十分重要的理论与现实意义。

众所周知,考察人口与经济之间关系的标准框架是Samuelson(1958)和Diamond(1965)提出的世代交叠模型(overlapping generations model,OLG)。然而Samuelson和Diamond发展的OLG模型假定人们只生活两期,即年轻工作和年老退休两个阶段,年轻是当期,年老退休是下一期。这就意味着每一阶段的长度大约是30年,而一些人口参数在这30年中必须设定为不变的,这种高度抽象的处理决定了其无法模拟生命的不确定性,从而使理论与现实世界的数据对比较为困难,其研究结论也仅限于提供一些经济学上的直觉。之后,Blanchard(1985)利用 Yarri(1965)的框架建立了一个连续时间OLG模型,得到了一些比较简洁有用的结论,然而其在模型处理上严重依赖于常数死力的假设,这样人口老龄化中的一个重要微观基础即寿命的延长(老年死亡率降低)就无法从模型中得到模拟。值得一提的是,对于人口增长和资本积累之间的关系,Diamond(1965)和Blanchard(1985)给出的结论都是两者成反向关系。d'Albis(2007)应用了OLG模型这一“新古典文献用来分析人口结构变化对经济影响的共同工具”,考察了出生率的外生变动对资本积累的长期影响,然而结果显示这种影响可正可负,缺乏稳健的结论。对此,Lau(2009)放弃了d'Albis(2007)中过多的数学内涵,而采用稳态均衡给出了数量评估,结果显示人口增长和资本积累之间有可能是正向关系,但在一般工业化国家人口增长率所处的区间内,Diamond(1965)和Blanchard(1985)给出的传统的反向关系依然保持。OLG模型近年来也被国内学者广泛应用于有关养老保险体制改革的研究(柏杰,2000;袁志刚和宋铮,2000)。何新华(2001)、封进(2004)以及蒋云赟(2010)等分别从最优储蓄、福利经济学等角度建立模型并推导得出一些重要结论。但总体而言,国内对长寿风险的研究起步较晚,研究重点集中在长寿风险对商业年金的影响和长寿风险证券化的简单介绍上,缺乏长寿风险和资本积累之间关系的深入研究。

对此,本文作了两方面的尝试。一方面,上述文献大多基于生育率下降所导致的人口增长率变化与资本积累之间的关系,但生育率的下降并不是决定资本积累的唯一变量,稳定和持续改进的成年死亡率才是更加重要的人口因素(Mason,2004),因此,我们将研究拓展到老龄化的另一个微观基础,即预期寿命延长与资本积累之间的关系。另一方面,d'Albis(2007)和Lau(2009)等文献只是给出了一般情形,并没有对退休和公共养老金体制进行具体的建模,本文在建立随机OLG模型时不仅考虑了用生存概率对终生效用进行折现,而且在一般均衡框架下纳入中国独特的混合养老金体制,以增强模型的针对性和实用性。

二、模型建立

从本文的研究主题可以看出,这里的建模目标不仅要考虑死力的连续改进以体现长寿风险的影响,还要考虑中国社会统筹和个人账户相结合的混合养老金体制。因此,我们先用效用最大化框架分析作为个人账户缴费主体的个人消费决策,然后用利润最大化原则考察社会统筹缴费主体的公司工资决策,再建立政府现收现支性质的社会统筹养老金模型以反映其联系缴费率和替代率的政策机制。最后因为摒弃了Blanchard(1985)的死力常数假设,我们不能在其框架下得到加总后人均消费的表达式,所以还需要建立人口模型模拟现实的人口学特征。

(一)个人消费

个人在时点t的终生期望效用为:

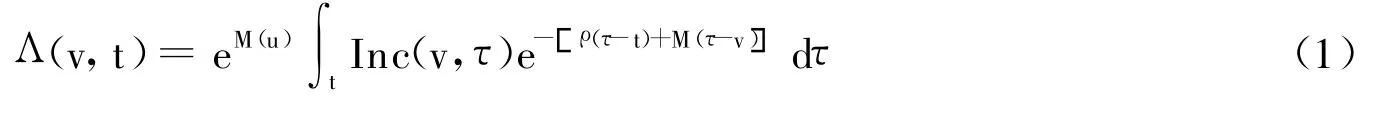
其中,v为出生时刻,u=t-v为个人在计划期间的年龄,效用采用特殊的对数效用形式U(c(v,τ))=Inc(v,τ),ρ是常数的时间偏好。由精算数学可知,m(s)ds为累计死力,而m(s)为即时死力,显然e-M(τ-v)为v时出生者在τ时仍然生存的概率。(1)式中的eM(u)来自于这样的事实:v时出生者在t时依然存活的条件下,一直生存到τ时(τ＞t)的概率是一个条件概率 ,即e-M(τ-v)/e-M(t-v)。

个人的预算约束为:其中,a(v,τ)为个人金融财产,a(v,v)=0且a(v,v+)≥0为最大生存年龄);r(v)为利率。对于r(v)+m(τ-v),我们采用Yarri(1965)的假设,即存在一个精算上公平定价的年金合同且个人金融资产皆以此种形式持有。N(v,τ)定义为v时参加工作的个人在τ时的劳动供给,即个人处于工作期间其值为1,处于退休期间为0。w(τ-v)为工资,lτ为我国社保个人账户中个人缴费占工资的百分比,p(v,τ)为社会统筹的退休给付,b为个人账户的退休给付额度。

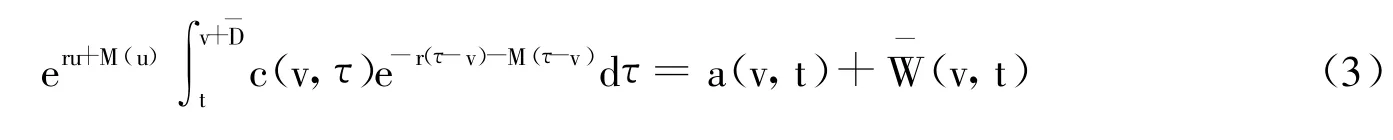
这样,问题就变为个人选择消费的时间路径去求基于预算约束(3)式的终生效用(1)式的最大化。运用与Blanchard(1985)相似的技术得到c(v,τ)的表达式,在(3)式中令 t=v并把c(v,τ)的表达式代入,经适当调整可以得到:

(二)公司

假定公司在完全竞争市场上生产同质的产品,生产函数为Yt=(ANt)1-α,其紧凑形式 yt=,其中 Y、K 、N 和 A 分别为产出、资本投入、劳动投入和技术水平,且技术进步的动态方程为A(t)=A(0)egt。按照我国统账结合的社保体制,公司是社会统筹的缴费主体,将按照其生产收益的比率η为职工缴纳社会统筹部分的养老金,这样代表性企业的未来利润就等于产出减去企业投资以及企业为职工工资和社会统筹养老金的支出(1+η)w(s),对于这个简单的利润最大化问题,我们容易得到:

(三)政府

按照我国城镇公共养老金体制,当期在职职工的社会统筹基金作为现收现付的养老金福利支付给当期仍然存活的所有退休职工,这样我们有:

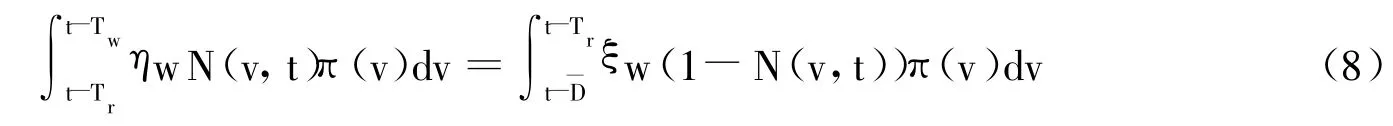
(8)式左边是当期在职职工所缴纳的养老金总和,右边是当期退休职工所得到的社会统筹养老金总和,其中ξ为社会统筹给付的替代率,Tr为退休年龄,π(v)为人口密度。(8)式可以简化为左右两边的积分项分别为当期工作人口总和和退休人口总和(TW为参加工作年龄,n为人口增长率,并且假定基期人口为1)。随着老年赡养比的增大,要保持替代率不变,社会统筹缴费比率必须上升;相反,社会统筹缴费比率不变,长寿风险必然造成替代率的下降。

(四)人口

如上文所述,由于摈弃了Blanchard(1985)的死力常数假设,就不能在其框架下得到加总后人均消费的表达式,这里利用从Lotka's(1939)中拓展的框架模拟现实的人口学特征。我们令B(v)为v时人口的出生婴儿数,则有B(τ)=B(v)en(τ-v),即人口出生数以n增长,这样两边都乘以生存概率并稍作变形就可得到τ时 τ-v岁的人口密度,即B(v)e-M(τ-v)=B(τ)e-n(τ-v)e-M(τ-v)。为方便起见,把人口密度记为π(v),可得到加总后的变量:

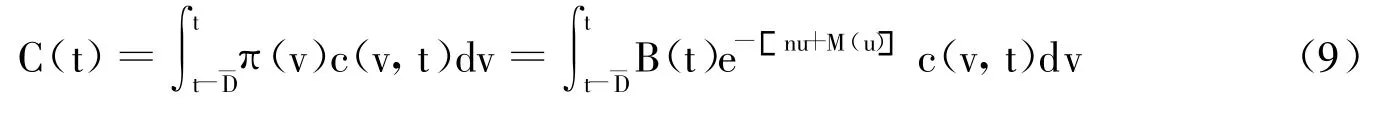
三、稳态均衡

稳态时,由(6)式和(7)式有:

对(4)式进行简单运算和整理,并令t=v,且考虑到工资是从开始工作时间Tw起领取的,我们可以得到:

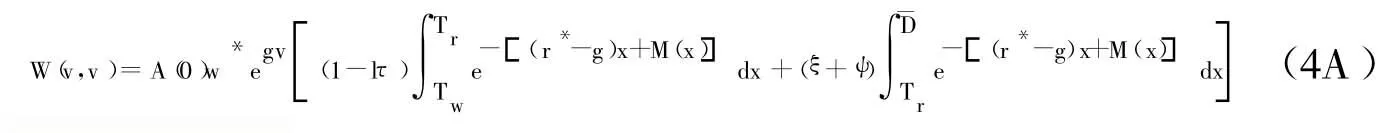
故(5)式变为:

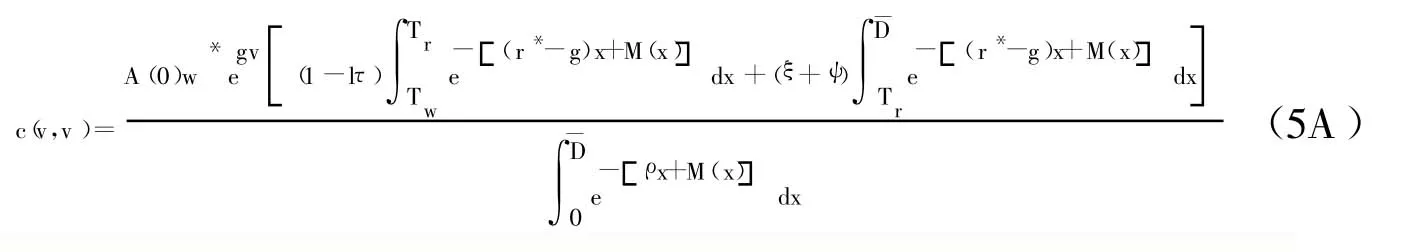
在任意时刻τ,商品市场的均衡要求商品的供给等于需求,也即:

由 k(τ)=K(τ)/(A(τ)N(τ))可得 :

其中,N(τ)是由劳动供给函数 N(v,τ)对人口密度加总而得,即N(τ)=B(τ)可见劳动供给的增长率等于人口增长率。把(11)式变形后代入劳动供给的表达式进行整理,当经济达到稳态均衡时有(τ)=0,可得:

其中,c(τ)=C(τ)/A(τ)N(τ)。把(9)式和加总后的劳动供给表达式代入c(τ),可以得到:

把(13)式和稳态工资表达式代入(12)式,由(6A)可知,(13)式中的r*也取决于k,故当其他参数的值确定后,式中唯一变量就是生存概率e-M(x),当预期寿命延长导致生存概率发生变化时,生存概率或预期寿命与k之间必然有一一对应关系,尽管我们无法给出简单的解析表达式,但可以通过下面的数值模拟得到结果。

四、数值模拟

(一)相关参数设定

当生产函数为柯布—道格拉斯形式时,国外文献一般把收入的资本份额设定为α=0.3(Barro等,1995),在以中国经济为范例的实证研究中,物质资本的贡献率在0.3—0.8之间(Chow和Lin,2002)。这里设α=0.35,技术进步率g=0.02,消费者偏好参数设定为ρ=0.02,社保参数根据国家相关政策规定,企业缴费率η=0.2,个人账户缴费率 lτ=0.08,社会统筹替代率ξ=0.35,个人账户替代率ψ=0.242,退休年龄Tr=60岁,最大生存年龄根据中国人寿保险业经验生命表设定为D-=105岁,参加工作年龄Tw设定为20岁(见表1)。

表1 生产函数和社保参数设定

(二)构造新的生命表

生存概率的参数设定是本文重点,目的是建立死亡率和预期寿命之间一一对应的关系,在此使用人口死力预测文献中广泛使用的Lee-Carter方法:

其中,mxt为x岁的人在t时刻的死亡率,ax为较近年份的自然对数死亡率,βx为ax中较近年份和之前某基期年份两点间自然对数死亡率的差值,θt为反映死亡率水平的时间趋势项,σxt为随机项。因为我们的目的是要建立死亡率和预期寿命之间的对应关系而不是预测,故可省略随机项而将(14)式写成:

由趋势外推模型可知寿命延长与θt的递增是等价关系,按此逻辑给θt取值即可模拟长寿的影响。这里我们把2000-2003年中国寿险业经验生命表中的各年龄死亡率自然对数分别作为(14A)式中的ax的值,再把2000-2003年和1990-1993年生命表中各年龄死亡率自然对数的差分别作为(14A)式中βx的值,这样θt与mxt、θt与预期寿命之间就建立起了一一对应关系。当θt=0.885时,由公式模拟可得到一张死亡率改善的新生命表,这样对θt反复取值使预期寿命每次增加大约2岁的跨度,最终得到五张生命表。这里的预期寿命和人口增长率采用联合国2008年发布的世界人口展望报告(World Population Prospects,2008)中的数据(见表2)。

表2 我国人口增长率与预期寿命对应表

利用(14A)式得到五张反映死力改善的生命表,将其和与之相对应的人口增长率代入(12)式进行计算,再结合其他上文设定的参数,这样(12)式就仅有一个未知数k,用EXCEL对方程两边进行反复试算直至相等,就可得出随着预期寿命延长而相应变化的k值(见表3)。

表3 预期寿命与资本积累(有统账结合的养老金体制)

表3显示数值模拟与理论分析的结论一致,即预期寿命和资本积累成正向关系,长寿风险的确会促使个人理性进而整个社会加强资本积累,以应对养老资源不足的挑战。

然而上述结论是在单一参数设定的情况下得出的,因此还需对生产函数、个人偏好和养老金体制中的三类参数进行稳健性分析。

对生产函数参数除了上文中采用的α=0.35之外,再令α=0.38,结果显示预期寿命和资本积累之间的正向关系依然成立(见表4),实际上当α在0.3-0.8间取值时这种正向关系都成立。对于个人时间偏好参数,稳健性检验的结果显示,当ρ在0-0.04之间取值时都不影响预期寿命和资本积累之间的关系,表4给出了ρ=0.03时的情形。对于养老金替代率参数的稳健性检验相当于做了仿真的养老金改革。方案一:没有养老金体制,结果显示不仅长寿风险和资本积累之间的关系没有改变,而且资本积累的额度要大于现行统账结合养老金制度下的资本积累额度,即现行养老金体制不利于资本积累(见表5);方案二:个人账户部分的个人缴费率和替代率不变,分别为8%和24.2%,而社会统筹部分的公司缴费率为20%,其中一半进入社会统筹,替代率变为17.5%(35%÷2),而另一半则进入个人账户,替代率参照个人账户的替代率变为30.25%(0.242×0.1/0.08),结果显示预期寿命和资本积累之间的正向关系依然成立,而且因增加了个人账户份额,资本积累的额度同样大于表3的结果(见表6)。

表4 生产函数和个人时间偏好参数的稳健性检验结果

表5 预期寿命与资本积累(方案一:无养老金体制)

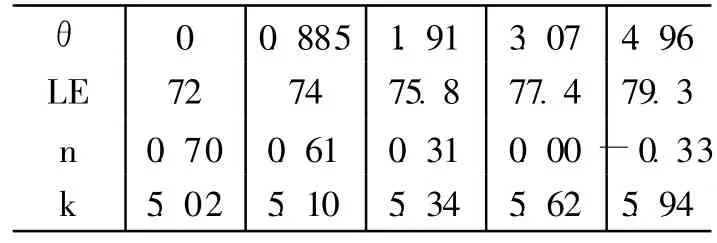
表6 预期寿命与资本积累(方案二:减少社会统筹,增加个人账户)

至此我们可以得出结论:稳态的人均资本和长寿风险之间的关系是正相关的,其对模型参数值的变化是稳健的,而且从中可以看出养老金体制安排在资本积累中所起的重要作用。

五、结 论

正如前文所述,长寿风险会成为改变人们消费储蓄模式的内在动因,促使人们增加资本积累以应对漫长的退休生活。我们利用OLG模型这一“新古典文献用来分析人口结构变化对经济影响的共同工具”,通过商品市场的均衡推导出包含资本积累的均衡方程,再利用重新构建的反映死力改善的新生命表和数值模拟的方法给出均衡时资本积累方程的数值解,结果表明预期寿命的延长对资本积累具有明显的正向影响。这一结论的经济学解释是直观的:当预期寿命延长时,如果退休年龄固定,人们的理性选择是增加储蓄以便为相对延长的退休生活筹备足够的资金,从而增加资本累积。而资本积累是经济增长的重要源泉,因此人们把这种由老龄化带来的意外之喜称为第二人口红利,可以说这是人口老龄化这一人类共同面临的难题本身所孕育的一种可能的解决方案。

在明确了长寿风险和资本积累之间的关系后,我们关注的另一个焦点就是养老金体制在预期寿命延长促进资本积累这一过程中所起的作用,因此我们将我国统账结合的混合养老金体制纳入模型,考察在现有体制安排下寿命增加对资本积累的影响。数值模拟的结果表明我国现有的养老金体制安排不利于资本的积累。我国的社会统筹是一种现收现付的养老金制度安排,由当前职工缴费支付当前退休职工的养老金福利,这种制度安排本质上是一种即期的代际间转移,中间基本没有储蓄投资等过程,因此可以认为它对资本积累没有影响。我国统账结合养老金体制中的个人账户本质上是一种强制储蓄,直接导致和促进资本积累。但是目前国际通行做法是社会统筹部分的替代率为社会平均工资的25%,个人账户占50%-60%,而我国社会统筹部分过高,为35%,个人账户部分却过低,只占24.2%,这显然不利于资本积累,模拟结果显示其资本积累的额度甚至要低于没有养老金制度安排的情形(比较表3和表5)。按照本文的模拟方案二进行调整,增加个人账户份额的同时减少社会统筹份额,则资本积累额度会明显提高。需要注意的是,长寿风险对个人账户偿付能力的压力大于社会统筹,因此探索一个最优的统账比例应该是今后养老金改革中需要重点考虑的问题。另外,与本文模拟结果相比,现实体制中的资本积累效果可能还要糟糕,因为作为资本积累主要制度安排的个人账户中尚未完全解决的空账问题会阻碍其功能的发挥,因此从促进资本积累应对长寿风险的角度看,实行个人账户的“实账化”运行以及社会统筹基金和个人账户基金的分离也是我国养老金体制改革的必要举措。

[1] 袁志刚,宋铮.人口年龄结构、养老保险制度与最优储蓄率[J].经济研究,2000,(11):24-32.

[2] 何新华.养老保险体制改革成本的最小化研究[J].世界经济,2001,(2):3-13.

[3] 封进.中国养老保险体系改革的福利经济学分析[J].经济研究,2004,(2):55-63.

[4] 蒋云赟.我国养老保险对国民储蓄挤出效应实证研究——代际核算体系模拟测算的视角[J].财经研究,2010,(3):14-24.

[5] Mason A,Lee R.Reform and support systems for the elderly in developing countries:Capturing the second demographic dividend[J].Genus,2007,62(2):11-35.

[6] d'Albis H.Demographic structure and capital accumulation[J].Journal of Economic Theory,2007,132:411-434.

[7] Blanchard O J.Debt,deficits,and finite horizons[J].Journal of Political Economy,1985,93:223-247.

[8] Blanchard O J,Fischer S.Lectures on macroeconomics[M].Cambridge,M A:MIT Press,1989.

[9] Diamond P A.National debt in a neoclassical growth model[J].American Economic Review,1965,55(5):1126-1150.

[10] Heijdra B J,Romp W E.A life-cycle overlapping-generations model of the small open economy[R].Research Report SOM 05C04,University of Groningen,2005.

[11] Heijdra B J,Romp W E.Ageing and growth in the small open economy[R].CESifo Working Paper No 1740,2006.

[12] Keyfitz N,Caswell H.Applied mathematical demography(third edition)[M].Springer Inc.,New York,2005.

[13] Lau S-H P.Demographic structure and capital accumulation:A quantitative assessment[J].Journal of Economic Dynamics and Control,2009,33:554-567.

[14] Samuelson P A.An exact consumption-loan model of interest with or without the social contrivance of money[J].Journal of Political Economy,1958,66(6):467-482.

[15] Yarri M.Uncertain lifetime,life insurance,and the theory of the consumer[J].Review of Economic Studies,1965,32(2):137-150.