一种齿面接触点柔度矩阵的计算方法
刘光磊,赵 宁,张瑞庭
(西北工业大学机电学院,陕西 西安 710072)
0 前言
在进行轮齿加载接触分析时,如何获得初始啮合点处接触椭圆长轴上离散点的柔度矩阵是关键技术之一。许多学者对此进行了研究[1-7],所提出的方法大致可以分为两种。一种是直接法[1-5],即直接采用有限元法进行分析;另一种是间接法,即先采用有限元法形成齿面网格柔度矩阵,经转换,得到轮齿接触椭圆长轴上离散点的柔度矩阵[6-7]。直接法计算结果精确,但计算过程复杂,花费时间长。间接法计算精度稍低,但计算速度快、适应面广。直接法已经成熟,间接法尚有待改进。
间接法在操作中,文献[6-7]提出了从齿面网格柔度矩阵向齿面接触点柔度矩阵转换的二元插值法,但并未给出具体插值的细节。为了实现从齿面网格柔度矩阵到齿面接触点柔度矩阵的转换,本文以有限元法中的数值计算原理为基础,提出从齿面网格柔度矩阵到齿面接触点柔度矩阵的混合插值法。在求解中发现,在齿面网格结点施加单位载荷时,相邻齿面结点出现齿面畸变。这与弹性力学中的布辛涅斯克的计算结果相左。在网格单元包含两个以上的接触点时,从网格结点向着它所包围的接触点所进行的位移插值,有可能出现接触点柔度矩阵主对角线不占优的情况。为了解决这一问题,提出了齿面网格结点间距与接触点间距必须协调,须保证一个网格结点单元只包含一个接触点。所提出的方法,物理概念清楚,可操作性强。
1 混合插值方法
1.1 弧齿锥齿轮有限元分析模型
本文采用弧齿锥齿轮单齿模型,齿轮副的工作面为小轮凹面和大轮凸面。边界条件为固定轮毂内表面和侧面,计算齿面网格结点的柔度矩阵时采用三维八节点非协调等参单元[8]。齿面加载接触分析有限元网格模型[9-10]如图1所示。
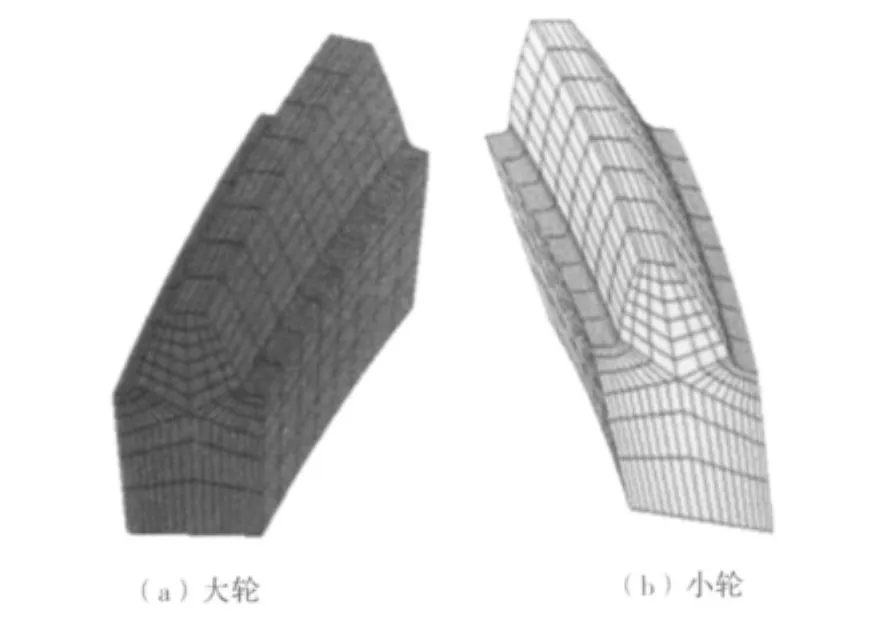
图1 轮齿有限元模型Fig.1 Finite element models of gear teeth
1.2 齿面网格柔度矩阵和齿面接触点柔度矩阵
齿面网格柔度矩阵用于反映齿面抵抗外加载荷变形的能力。依次对齿面上的每个网格结点施加单位法向载荷,求得每次加载时齿面所有结点沿该处法线方向的位移,也就是各结点的柔度系数,将它们按行排列,即可组成齿面网格柔度矩阵。图1中的轮齿工作齿面上共有N个结点,则齿面网格柔度矩阵为
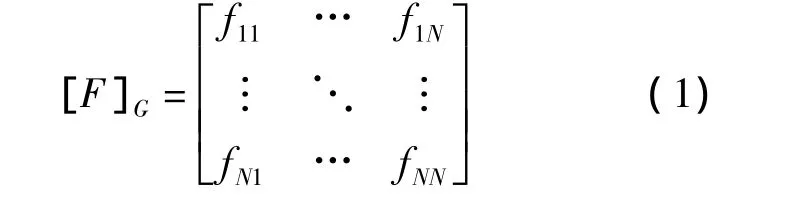
式中,脚标G为齿面网格;矩阵中的元素fij为在网格结点j作用单位载荷时网格结点i产生的位移。
齿面网格柔度矩阵反映了作用在轮齿齿面上各结点的载荷与变形关系,而在弧齿锥齿轮加载接触分析过程中,需要用到反映接触椭圆长轴上离散点的载荷与变形关系,即接触点柔度矩阵。
接触点柔度矩阵的含义与齿面网格柔度矩阵相同,即依次对各接触点加载时,求得每次加载时所有接触点沿法线方向的位移,也就是各接触点的柔度系数,将它们按行排列,即可组成齿面接触点柔度矩阵。
设齿面瞬时接触椭圆长轴上的离散点有n个,按照接触点柔度矩阵的定义,可得齿面瞬时接触椭圆长轴上离散点的柔度矩阵为
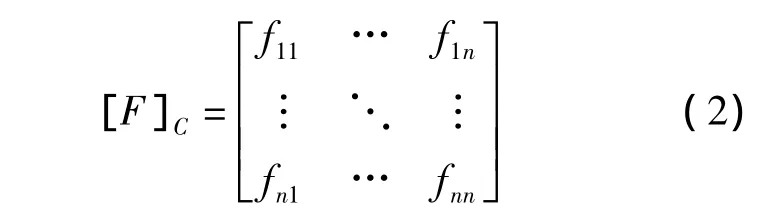
式中,脚标C为齿面接触点;矩阵中的元素fij为在接触点j作用单位载荷时接触点i产生的位移。
1.3 混合插值方法
从[F]G与[F]C的定义可知,尽管两者物理含义相同,但不能通过简单的网格点加密插值,实现从齿面网格柔度矩阵到接触点柔度矩阵的转换,而要依据柔度矩阵的力学含义,基于有限元数值计算原理,实现两者的转换。
为了在保证精度的前提下简化计算,将齿面网格和接触椭圆长轴上的离散点,转换到齿轮的旋转轴截面中,如图2所示。图中○表示网格结点,□表示椭圆长轴上的接触点。具体插值分两步完成。
第一步,载荷等效即形成包围接触点的网格结点的等效结点载荷系数。以图2中左边第一个接触点为例,设想在该点施加单位法向载荷,按照虚功原理,将该载荷等效转换到包围它的四个网格结点上,即
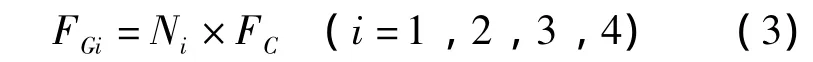
式中,FC为接触点单位法向载荷;Ni(i=1,2,3,4)为四个网格结点的形函数在接触点处的值;FGi为等效载荷。因为FC为单位载荷,所以FGi也就是等效载荷系数。
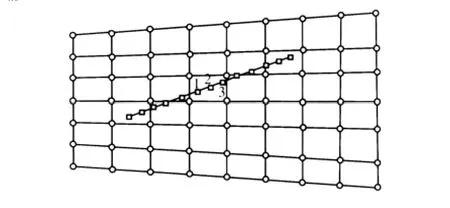
图2 齿面网格旋转投影示意图Fig.2 Schematic of rotary prejection of tooth surface grid
这里的形函数采用双线性等参数单元,即
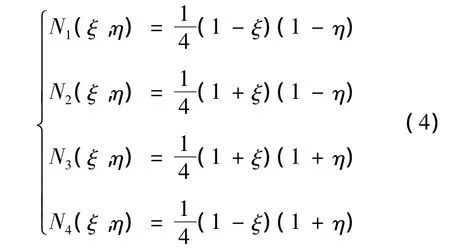
式中,(ξ,η)为局部坐标,如图3所示。
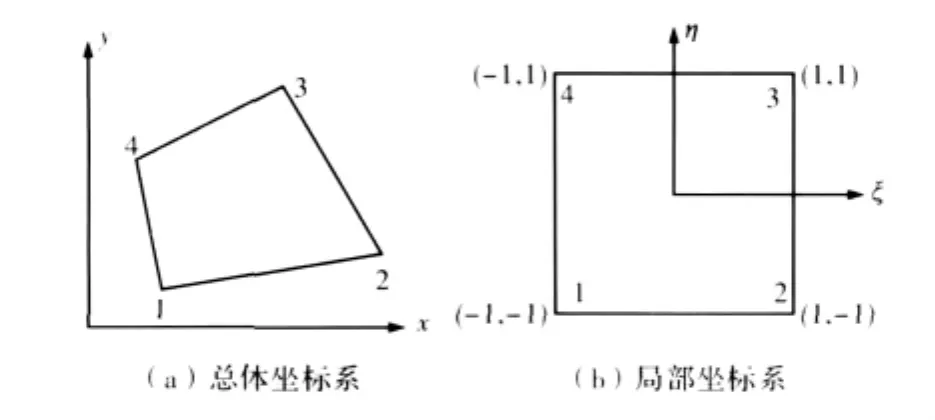
图3 单元坐标系Fig.3 Element coordinate system
与网格结点相关的形函数定义于局部坐标系中,而实际齿面网格结点和接触点都定义于总体坐标中,如图2和图3所示。为了计算形函数在接触点处的值,需要建立如下坐标变换关系:
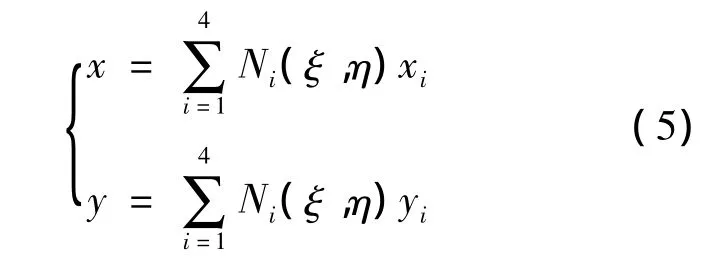
式中,(xi,yi)为网格结点坐标;(x,y)为接触点坐标。将(xi,yi)和(x,y)代入上式,解之,得到与(x,y)对应的(ξ,η),再带入式(4),即可求得Ni(i=1,2,3,4)。
第二步,位移插值即从齿面网格柔度矩阵出发,计算接触点的柔度系数,形成齿面柔度矩阵。在计算时假设轮齿为线弹性、小变形,因此可以采用叠加原理。
在接触点施加单位载荷后,各接触点均会产生变形。在得到包围施加单位载荷的接触点的网格结点的等效载荷系数之后,就可以应用叠加原理,将网格结点的变形等效为接触点处的变形,即
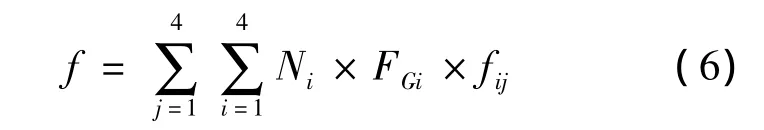
式中,对i的求和,表示在同一网格结点施加等效载荷时,对接触点的插值;对j的求和,表示包围同一接触点的四个网格结点在接触点的插值之和。
依次对各接触点施加单位法向载荷,采用上述载荷-位移混合插值方法,即可得到单齿接触点的柔度矩阵。将相互啮合的轮齿接触点柔度矩阵相加,最终得到轮齿加载接触分析(LTCA)所需的接触点柔度矩阵。
2 齿面网格柔度矩阵的畸变
得到齿面网格柔度矩阵以后,图形显示其计算结果。图4和图5为大轮凸面上靠近小端处的网格结点受到法向单位载荷作用时,整个齿面及其局部的变形情况。

从图5可以看出,沿着齿长方向分布的5个结点1、2、3、4、5,加载点3的变形最大,结点2和4的变形比结点1和5的变形小,但它们却比结点1和5更靠近加载点3,即齿面出现畸变。齿面畸变有可能导致接触点柔度矩阵的非对角元出现负刚度,从而影响接触点载荷的分布。这种现象与弹性力学中的布辛涅斯克的计算结果相左。为此,作者将有限元模型导入到Ansys中,计算齿面网格在某点施加法向单位载荷时的齿面变形,如图6所示。
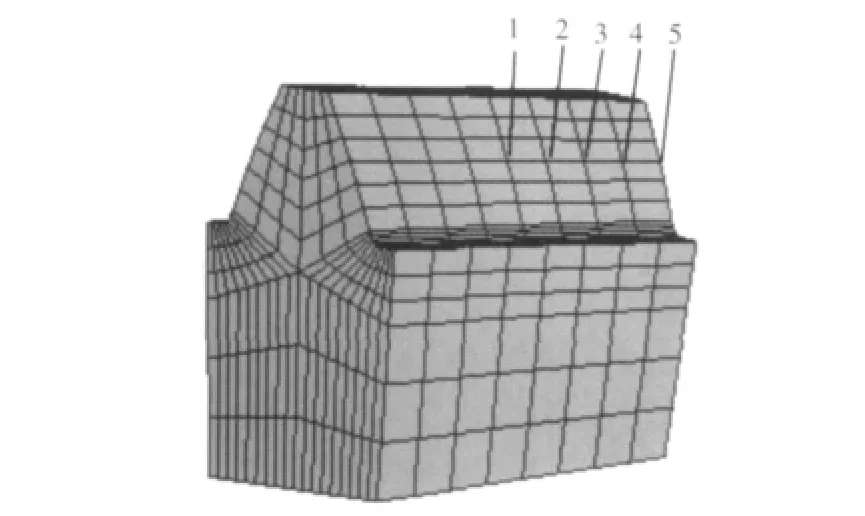
图6 Ansys中分析大轮轮齿模型Fig.6 Ansys analysis model for bull wheel gear tooth
计算结果如下:加载点3与图5中加载点对应。结点1、2、3、4、5点的法向位移见表1。

表1 Ansys齿面变形计算结果Table 1 Results of tooth distortion calculated with Ansys ×10-6
由以上数据可以看出,Ansys有限元分析结果也存在齿面畸变的现象。
在齿面上其他网格结点加载时,也发现类似齿面畸变现象。
3 接触点柔度矩阵主对角线不占优及解决方法
当网格结点间距过大时,一个单元内可能包含多个接触点。如图2所示,接触点1、2、3同时落在一个网格单元内。按照前述载荷-位移插值法,计算接触点柔度矩阵时,因载荷与位移插值分别进行,有可能导致接触点柔度矩阵主对角线元素不占优。这不符合柔度矩阵应有的物理意义。
以图2中的接触点1、2、3为例。设它们的局部坐标分别为(-0.25,-0.25)、(0.25,025)和(0.75,0.75)。当对第二个接触点作用法向单位载荷时,从已知的齿面网格结点柔度矩阵中提取该网格单元结点的柔度系数为
把三个接触点的局部坐标带入式(4)分别得到三个接触点的形函数为

把接触点2的形函数带入式(3),得到等效载荷系数为
FGi=[0.1406 0.2344 0.3906 0.2344]
将上述数据分别代入式(6)得到三个接触点的位移值分别为
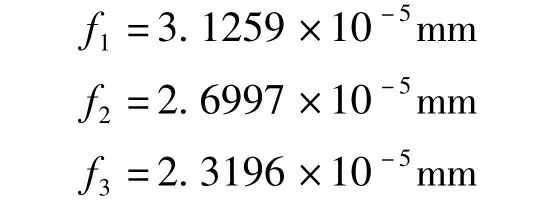
由计算结果可以看出,加载接触点2的变形已经小于同一网格单元内的接触点1的变形。说明柔度矩阵的主对角线元素已经不再占优。
要解决接触点柔度矩阵主对角线不占优的问题,就要密化齿面网格,使一个单元内最多包含一个接触点,如图7所示。从而避免出现柔度矩阵主对角线不占优的现象。
为了保证计算符合物理意义,同时兼顾计算效率,密化网格的尺寸应与接触点距相协调。以一个网格单元正好包含一个接触点,且相邻接触点落在相邻网格单元为宜。
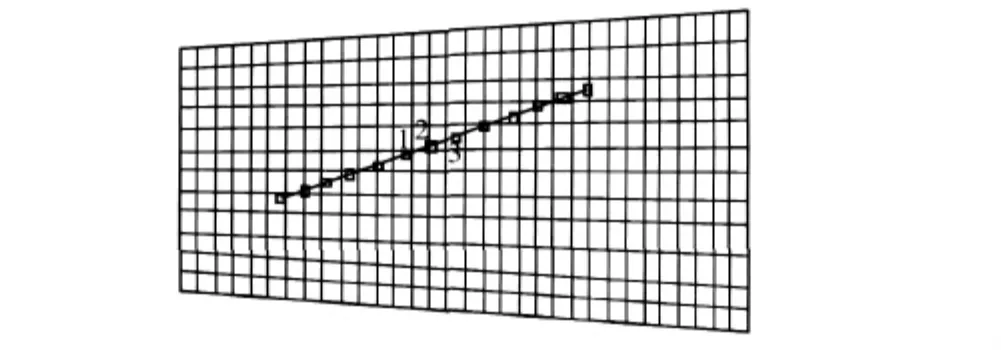
图7 密化后的齿面网格Fig.7 Tooth surface grid after densification
4 结论
(1)本文提出了一种由齿面网格柔度矩阵计算齿面接触点柔度矩阵的载荷-位移插值方法。
(2)在求解齿面网格柔度矩阵时,发现了齿面网格结点位移畸变现象。
(3)采用载荷-位移插值时,可能导致齿面接触点柔度矩阵的主对角线不占优。为此,应使齿面网格单元的尺寸与接触点距离相协调,保证一个网格单元仅包含一个接触点。
[1] BIBEL G D.Contact stress analysis of spiral bevel gears using finite element analysis[J].ASME Journal of Mechanical Design,1995,117(2):235-240.
[2] LITVIN F L,FUENTES A,HAYASAKA K.Design,manufacture,stress analysis,and experimental tests of low-noise high endurance spiral bevel gears[J].Mechanism and Machine Theory,2006,41(1):83-118.
[3] 唐进元,蒲太平.弧齿锥齿轮动态啮合有限元数值分析[J].机械科学与技术,2009,28(8):981-985.
[4] 郑昌启.螺旋锥齿轮轮齿加载接触分析计算原理[J].机械工程学报,1993,29(4):50-54.
[5] 李润方.运转中啮合轮齿的三维应力应变数值分析及实验研究[J].机械工程学报,1994,30(2):38-44.
[6] 方宗德.齿轮轮齿承载接触分析(LTCA)的模型和方法[J].机械传动,1998,22(2):1-3.
[7] 田行斌.弧齿锥齿轮的有摩擦承载接触分析[J].西北工业大学学报,2000,18(1):19-22.
[8] 刘更.结构动力学有限元程序设计[M].北京:国防科技大学出版社,1993.
[9] LITVIN F L.Computerized design,simulation of meshing,and contact and stress analysis of facemilled formate generated spiral bevel gears[J].Mechanism and Machine Theory,2002,37:441-459.
[10] 刘光磊,樊红卫.含齿根过渡曲线的弧齿锥齿轮有限元精确建模[J].机械科学与技术,2010,29(12):1595-1601.

