圆柱壳内曲面椭圆裂纹应力强度因子数值计算
(1.武汉工程大学机电工程学院,湖北 武汉 430074;
2.中国石化股份有限公司武汉分公司,湖北 武汉 430082)
圆柱壳内曲面椭圆裂纹应力强度因子数值计算

(1.武汉工程大学机电工程学院,湖北 武汉 430074;
2.中国石化股份有限公司武汉分公司,湖北 武汉 430082)
采用节点法,在裂纹前沿设置三维奇异单元,建立了求解圆柱壳内埋曲面椭圆裂纹应力强度因子的断裂力学有限元模型.对裂纹前沿各点应力强度因子进行了分析,得出了应力强度因子的变化曲线并确定了最大应力强度因子所在位置为出现氢腐蚀分层现象的化工设备的安全评估提供了重要的依据.
氢腐蚀;节点奇异单元;曲面椭圆裂纹;应力强度因子;有限元法
0 引 言
某石化公司在设备检修时,发现一换热器的壳体内表面多处存在着交叉裂纹,裂纹处的表面有突起现象,如图1所示.将此处取样并沿厚度方向剖开,发现在壳体中面附近已产生严重的分层情况,如图2所示.由于石化行业许多设备处于湿硫化氢环境中,会发生氢腐蚀破坏:氢进入钢中与碳结合生产甲烷,甲烷气体的聚集会在局部产生很大压力从而造成壳体分层[1-2],图2所示的情况就是氢腐蚀引起的分层现象.为便于对这种氢腐蚀分层现象进行断裂力学分析,可将其简化为壳体壁厚方向中面内的曲面椭圆形裂纹,如图3所示.从换热器壳体取样试件看到,随着中面处椭圆裂纹面的增大,筒体的内表面发生突起现象,内表面上的交叉裂纹会进一步扩展并引起材料的失效,严重影响设备的安全运行.当设备内装有易燃易爆的介质时,一旦发生失效,就会引发非常严重的安全事故.
目前国内外主要是从材料失效方面来研究氢腐蚀问题[3-5],采用断裂力学分析方法进行研究的较少[6],特别是对圆柱壳内埋曲面椭圆裂纹的研究还未见相关文献报道.应力强度因子是断裂力学里最重要的参数之一,它是判断含宏观裂纹体在载荷作用下是否发生裂纹扩展的主要参量.对于三维曲面裂纹问题,其应力强度因子的分析比二维裂纹问题难得多[7-10],到现在还没有一个准确的解析解.因此,通过在裂纹尖端设置奇异单元建立了三维曲面椭圆裂纹的有限元分析模型,对裂纹前沿各处的应力强度因子进行了数值计算,得到了应力强度因子沿裂纹前沿的变化曲线.

图1 换热器内表面产生的裂纹Fig.1 The crack developed on the inner on surface of heat exchanger

图2 内表面裂纹处厚度方向剖面情况Fig.2 The section of thickness-direction the inner surface crack

图3 换热器壳体分层现象简化示意图Fig.3 The simplified schematic drawing of layered heat exchanger shell
1 三维曲面椭圆裂纹的有限元建模
对于二维裂纹有限元分析软件可以自动生成奇异单元,而对于三维裂纹其奇异单元必须手动生成.建模时采用自下而上的建模方法,先建立节点,再由节点连接生成单元.由于换热器壳体氢腐蚀引起的分层现象产生的曲面椭圆裂纹的几何模型和受力分布在空间上均呈对称性,故只用建立壳体有限元分析模型,如图4所示.根据试件的解剖情况,椭圆裂纹长半轴为45 mm,短半轴在YOZ面上的投影长30 mm,壳体外径为1 200 mm,壳体壁厚为14 mm.

1.1 建立裂纹尖端处奇异单元
1.2 裂纹开裂面的模拟及整体模型的生成
如图6所示,有限元模型在开裂处有两个节点,这两个节点的空间位置相同但没有被连在一起,是相互独立的,并分别属于上下两边的单元,这样有限元模型在受载荷的作用时这两个节点就会沿开裂面裂开,由此来模拟裂纹的开裂.中心点及其左边的单元是不开裂的,在这里共用一个节点.

图5 裂纹尖端奇异单元Fig.5 Singular element of the crack tip

图6 裂纹尖端的开裂面Fig.6 Cracking surface of the crack tip
建立裂纹尖端的奇异单元后,就能很快完成整个模型,如图7所示.

2 模型求解
2.1 施加边界条件
有限元分析中采用材料的机械性能为:弹性模量E=2×105MPa,泊松比为μ=0.3.
位移边界条件:假设模型在X、Y、Z三个方向的位移分别用u、v、w表示.如图4所示,在面1和面2上v=0,在面3上w=0.
力边界条件:在筒体内表面施加1.6 MPa的内压,筒体端面(见图4)上施加24 MPa的拉应力,在椭圆裂纹面上分别施加30 MPa、40 MPa、50 MPa和60 MPa四种情况的压力.加载后的模型开裂情况,如图8所示.

图8 换热器壳体开裂图Fig.8 The cracked heat exchanger shell
2.2 计算应力强度因子
施加边界条件求解后,就可以得到裂纹前沿各处的应力强度因子,如表1所示,其中θ为椭圆裂纹前沿上一点在YOZ平面内与Z轴的夹角(如图4所示).根据表1的结果可以作出椭圆裂纹前沿应力强度因子的变化曲线图,如图9所示.
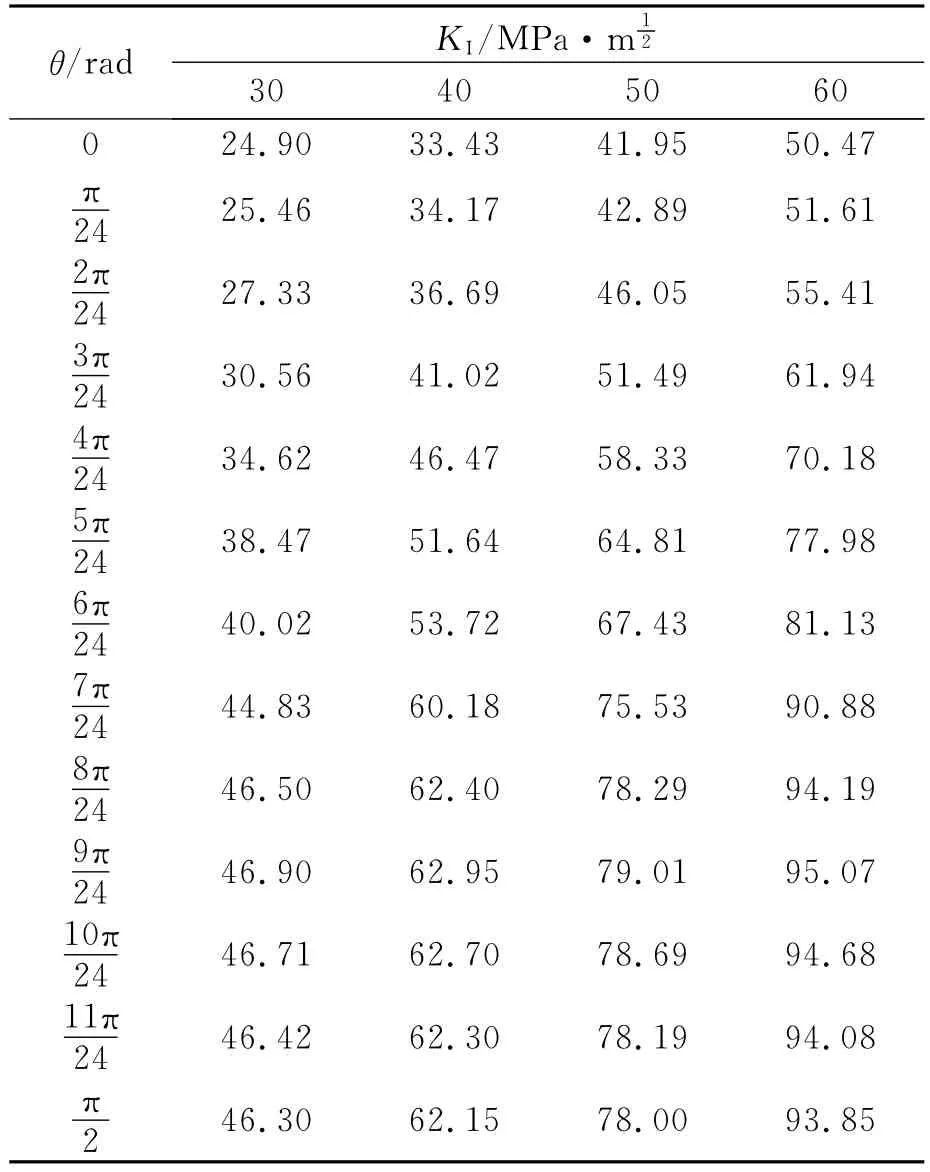
表1 裂纹前沿各点的应力强度因子K ITable 1 The stress intensity factors K I of the points in the front edge of crack

图9 应力强度因子变化曲线Fig.9 The variation curve of stress intensity factor
I时,KI达到最大值,随着θ继续增加,KI值开始减小但不明显;当θ一定时,随着裂纹面压力的增加KI随之增大.根据这一结果可以推测,若曲面椭圆裂纹要继续扩大,则在θ=处附近的K值最先I达到平面应变断裂韧度KIC,即裂纹在该处最先向前扩展.由于应力强度因子是判断裂纹是否扩展的主要参量,而在目前又无法得到曲面椭圆裂纹前沿应力强度因子解析解的情况下,通过数值模拟的方法求出椭圆裂纹前沿各点应力强度因子的近似解,再结合平面应变断裂韧度KIC的变化规律及裂纹扩展判据KI≥KIC,就可以定量的判断裂纹扩展情况,这一结论对换热器出现氢腐蚀分层后的在线监测及安全评估有着重大的指导意义.
3 结 语
a.通过节点建模法建立了含三维曲面椭圆裂纹的换热器壳体有限元模型.
b.通过有限元法计算出裂纹前沿各点的应力强度因子KI的数值解,将它们进行对比并作出其随角度θ的变化曲线,通过曲线能确定最大应力强度因子KI所在的位置.
c.本文的曲面椭圆裂纹应力强度因子解法可用于化工设备氢腐蚀破坏的安全评估中.
[1]谢育辉.加氢反应器和换热器高温腐蚀与对策[J].石油化工腐蚀与防护,2003,20(4):12-16.
[2]朱明伟.苯乙烯装置TT-201换热器腐蚀分析及防护对策[J].石油化工设备技术,2007,28(2):28-29.
[3]REN X C,ZHOU Q J.A Nucleation Mechanism of Hydrogen Blister in Metals and Alloys[J].Metallurgical and Materials Transactions A,2008(39):87-97.
[4]REN Xuechong,ZHOU Qingjun.The mechanism of nucleation of hydrogen blister in metals[J].Chinese Science Bulletin,2007,52(14):2000-2005.
[5]乔亮.球罐氢鼓泡形成原因及防护措施[J].石油化工腐蚀与防护,2006,23(2):51-53.
[6]何家胜.晶界损伤对裂尖应力场的影响分析[J].武汉工程大学学报,2008,30(3):87-89.
[7]蒋文春.湿H2S环境下16 MnR钢氢鼓泡的有限元模拟[J].吉林大学学报:工学版,2008,38(1):61-65.
[8]武小海.基于ANSYS的裂纹尖端应力强度因子研究[J].机械工程师,2011(1):42-43.
[9]何家胜.压力容器开孔接管处表面斜裂纹应力强度因子数值分析[J].核动力工程,2010,31(5):1-8.
[10]李莉.斜置半椭圆表面裂纹应力强度因子分析[J].石油矿场机械,2011,40(2):16-19.
[11]李翠华.计算应力强度因子的奇异单元法[J].西安交通大学学报,1991,25(6):23-28.
Numerical calculation for stress intensity factor of curved surface elliptical crack buried in cylindrical shell
HE Jia-sheng1,XIE Fei1,ZHU Xiao-ming2,CHEN Wei2,LU Yuan-ming2
(1.School of Mechanical Engineering,Wuhan Institute of Technology,Wuhan 430074,China;
2.Wuhan Subsidiary company,China Petrochemical Co.Ltd.,Wuhan 430082,China)
A finite element model of fracture mechanics was established to calculate the stress intensity factor(SIF)of curved surface elliptical crack buried in cylindrical shell by using the method ofdisplacement of the finite element setting 3D singular elements along the front edge of crack;the SIF of the points in the front edge of crack was analyzed,the variation curve of SIF was obtained and the location of the maximum SIF was discovered which provides an important basis for security assessment of the layered chemical equipments caused by hydrogen corrosion.
hydrogen corrosion;displacement of finite element;curved surface elliptical crack;stress intensity factor;finite element method
陈小平
TQ050.9
A
10.3969/j.issn.1674-2869.2011.11.018
1674-2869(2011)11-0070-04
2011-10-08
何家胜(1958-),男,湖北武汉人,教授,硕士.研究方向:压力容器结构强度与失效分析研究.

