基于N-S方程和自由转捩预测耦合求解的钝后缘翼型气动性能计算
邓 磊,乔志德,杨旭东,熊俊涛
(1.西北工业大学翼型、叶栅空气动力学国家级重点实验室,陕西西安 710072;2.机械与航空与太空工程系,加州大学欧文分校,CA 92697-3975)
0 引言
在风力机叶片气动性能预测和外形设计中,展向使用翼型的空气动力学特性是重要的参数,其准确性和完备性对叶片性能预测和设计具有重要的意义,因此可靠的翼型气动数据的准备通常是设计开始阶段花费时间最多也最困难的部分[1],而且翼型气动数据的误差甚至被认为是风轮载荷和性能预测中最大的误差来源[2-4]。
近年来,为改进厚翼型的气动性能和结构效率,研究者提出了钝后缘翼型的概念[4-7],这类翼型表现出气动和结构效率方面的双重优点。在结构方面,与相同最大相对厚度翼型相比,这类翼型增加了截面面积和截面上的转动惯量;气动方面,钝后缘增加了翼型的最大升力系数和升力线斜率,并减小了对前缘粗糙的敏感度[7-9]。这类翼型可以使一部分压力恢复发生于尾迹部分,因此减小了吸力面的逆压梯度,从而减缓了附面层的分离趋势,对光滑和粗糙翼面均提高了升力特性[10]。但是同时由于钝后缘后的脱体涡的存在,使翼型阻力有非常大的增加,给此类翼型的使用带来风险。由于受风洞实验阻塞度的限制,这类翼型公开发表的实验数据很少,且多为低雷诺数的实验数据[6-8,11],而实际大型风力机翼型的工作雷诺数通常在1×106~1×107之间;因此CFD数值模拟对这类翼型的设计和使用变得尤为重要。近年来国外使用几十万甚至将近百万网格数对这类翼型进行了CFD数值求解,但是一般使用固定的转捩位置作为流场计算的输入,没有考虑转捩位置的时均效应[7,10-14]。国内对这类翼型的研究较少:没有查到公开发表的实验结果,多为基于商业软件的数值求解[15-17];且一般后缘厚度较小,在2%相对厚度左右,实际大型风力机后缘厚度有时达到20% ~50%相对厚度。
本文基于RANS方程和线性稳定性分析的en转捩预测程序对有实验结果的风力机翼型进行了气动性能计算。通过对DU97-Flat翼型的计算分析了耦合过程和网格数对结果的影响;计算了DU97-W-300翼型的气动性能并和风洞实验结果进行了比较。
1 流场分析
本文采用二维定常RANS方程作为流场分析程序。求解N-S方程空间离散采用格心格式的有限体积法,时间推进采用五步Rungle-Kutta格式,引入二阶、四阶人工粘性项并使用当地时间步长、隐式残值光顺、三重网格等加速收敛技术。湍流模型采用一方程的Spalart-Allmaras(S-A)模型。
2 转捩位置计算和转捩流模型
转捩位置计算使用基于线性稳定性分析的en方法,这也是目前使用最普遍的可行的转捩预测方法。扰动放大系数计算公式为:

其中,ξ为沿物面的弧长,-αi为给定频率下求得的空间放大率,R为当前位置雷诺数。计算中由失稳点向后计算一组频率的放大曲线(本文计算15条),找出临界频率及对应的放大系数n达到临界放大因子的位置,即为转捩位置。
为消除或减弱“点转捩”引入的数值扰动,本文使用了转捩过渡区模型。由于考虑了有层流分离的转捩问题,本文选用Walker的模型,这种模型对于有分离的转捩过渡区模拟较好[18]:

其中:ReΔX为基于转捩过渡区长度ΔX的雷诺数,ReXtr为基于转捩位置Xtr的雷诺数。
有适当转捩过渡区长度后,涡粘性表达为:

其中:εtrans为过渡区的涡粘性系数,γtr为间歇因子,在0~1之间,ε为涡粘性系数。
3 网格数影响
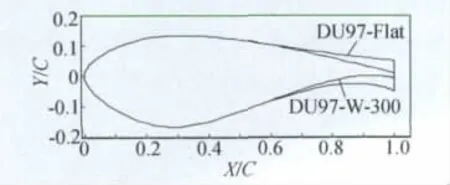
图1 DU97和DU97-Flat外形Fig.1 Airfoil shapes of DU97 and Du97-Flat
为考查网格数对计算结果的影响,并找到可以得到一定精度的气动特性并且尽量减少计算花费,使用由DU97-W-300翼型通过在弦线50%往后对称增加厚度得度得到的DU97-Flat钝后缘风力机翼型作为算例进行计算[19]。DU97-Flat翼型后缘厚度10%弦长,改形翼型和基本翼型外形如图1所示。计算状态:马赫数0.165,雷诺数3.0 ×106,攻角 α =0°,上、下表面转捩位置分别固定于0.343 和0.320。
此前的研究中,为方便网格生成,一般对有钝后缘翼型使用O-网格,对尖后缘使用C-网格。本文由网格生成程序Gridgen生成C网格,来计算钝后缘翼型。在网格生成时,将后缘处的直角稍作光顺,以改善在直角处的网格质量,这也是对此类翼型网格生成所常用的方法[7,10,11,20]。由于本文使用 RANS 方程和转捩预测程序耦合迭代的方法来求解,求解RANS方程得到附面层方程求解所需要的附面层外边界的压力或者速度分布,而附面层参数的精度直接影响到转捩预测的精度,因此附面层内的网格数在本文中有更重要的意义;垂直壁面方向的网格数应满足在附面层内有60左右的网格,因此在生成网格时,第一层网格距壁面1.0×10-6,内侧60层网格等间距分布。
为便于比较网格数对计算结果的影响,使用一系列的C-网格来计算。表1为网格分布比较,图2为352×96网格的分布。

表1 网格分布Table 1 Different computational grids

图2 计算网格352×96Fig.2 Computational Grid of 352 ×96
图3为计算的升力系数随网格数的变化关系。可以看出随网格数的增加,升力系数逐步趋于一个收敛值,但是在网格数更高时,升力系数又有所增加。在计算中,似乎使用更多的网格可以更准确地计算气动性能,但是随之而来的是计算花费的急剧增加,特别是本文使用RANS方程和转捩位置耦合迭代,计算花费对网格数的依赖关系更加明显,因此需要在计算精度和计算花费中间折中。本文以下的计算使用448×112网格。
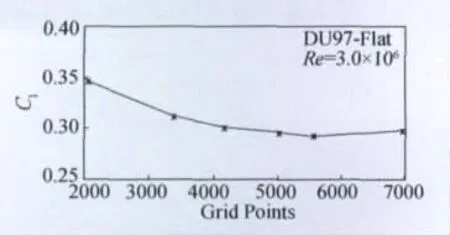
图3 升力系数随网格数变化Fig.3 Comparison of lift coefficient for different number of grid points
4 耦合求解
此前的钝后缘气动性能计算中,一般使用某个转捩位置计算程序,计算出转捩位置坐标后代入到RANS方程求解器中[7,10,20]。但是由于钝后缘处的涡脱落使翼型表面的压力分布表现出周期性的脉动,而使用这种固定的转捩位置没有考虑这种周期脉动的效应对转捩位置计算的影响,因此Standish K.J.等建议使用有时均性的转捩位置模型。本文耦合二维RANS方程求解和基于线性稳定性分析的en转捩位置计算方法,计算钝后缘翼型的气动性能。此前对定常流场的耦合过程中,通常是将流场计算至某个流动参数相对迭代次数的导数为常数时,而后调用转捩位置计算[21-22]。本文中由于钝后缘处的流场的非定常,不能得到收敛的流场解,因此为在转捩位置计算中考虑周期脉动的时均性,使用下面的耦合方法:
1)首先给一个初始的转捩位置代入RANS方程计算中。建议初始转捩位置在距前缘位置的远下游,比如80%弦长或者后缘处;
2)使用这个固定的转捩位置迭代计算RANS方程,至最大迭代次数Cyclemax,此时流场已经进入周期脉动;
3)继续计算流场Δkcyc次,并求解Δkcyc内的平均压力分布以及平均附面层外边界压力和速度分布;
4)将计算的附面层外边界速度和压力分布作为输入条件,调用附面层方程的求解程序,计算得到附面层参数和速度型;
5)使用计算得到的附面层参数和速度型作为输入条件,进行附面层流动的稳定性和转捩位置求解。在从失稳点向下游进行转捩位置计算的同时,判断是否出现了由于逆压梯度过大产生的层流分离,如果发生了层流分离则不再继续向下游进行转捩位置计算,而以层流分离点作为转捩位置。但是,此时计算的(j表示转捩位置迭代的次数)被认为是欠松弛的,即:实际用于RANS方程使用的转捩位置坐标位于的下游,用下面的方法来确定:

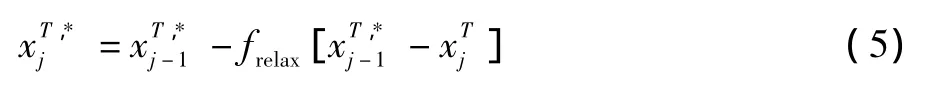
其中,frelax为 0.7。
这样,就完成一次转捩位置耦合迭代过程。
本文求解中,初始转捩位置上、下表面均设置为0.8,流场迭代1500次后,计算200次流场的平均压力分布;以后每200步调用一次转捩预测程序。图4为转捩位置随转捩位置迭代次数的关系,可以看出,转捩位置在10次迭代之内,就可以达到收敛。

图4 转捩位置收敛过程Fig.4 Convergence history of the transition locations

图5 气动性能收敛过程Fig.5 Convergence history of lift and drag coefficient
图5为升力系数和阻力系数随迭代次数的关系。可以看出随迭代的进行,升力系数和阻力系数均可以收敛到一个值,同时也可以看出,气动特性和转捩位置的依赖关系,也验证了进行转捩位置迭代的必要性。
5 气动性能计算
大雷诺数的钝后缘翼型风洞实验数据很少,1999年Timmer等发表了一个DU97-W-300翼型雷诺数为3.0 ×106的风洞实验数据[23]。DU97-W-300 翼型最大厚度30%,后缘厚度1.74%弦长,相比于其他钝后缘翼型相对较尖。本文计算网格448×112,计算状态马赫数为0.165,雷诺数 3.0 ×106。
文献[12]使用RANS方程求解器SACCARA程序,进行了DU97-W-300翼型的计算,但是使用了将近40万的网格,而转捩位置是使用Xfoil程序求解出转捩位置,而后作为固定转捩代入流场求解器中。本文进行了耦合求解并和[12]文计算结果作了比较。图6为本文计算结果和Xfoil计算的转捩位置的比较,可以看出在攻角较小时下表面转捩位置吻合较好,但是随攻角增加差别逐渐增大;本文计算的上表面的转捩位置小于Xfoil计算结果,特别是本文计算中,在12°就发生了前缘分离,而Xfoil计算显示还有10%弦长左右的层流。图7为本文CFD计算结果和实验结果以及文献[12]计算结果的比较。可以看出,升力系数在线性段和实验结果吻合很好,且比参考文献结果吻合好;但是和文献结果一样,失速迎角没有捕捉到。力矩系数可以看出,在13°之前本文计算结果和实验值吻合很好。为考察阻力计算的精度,图8为计算结果、实验结果和文献结果的极曲线的比较。可以看出,在低阻范围内阻力系数和实验值吻合较好。
6 结论
本文耦合RANS方程求解和转捩位置预测程序,进行了大厚度钝后缘风力机翼型气动性能计算研究。可以得到如下结论:
(1)通过分析网格数对计算结果的影响,可以看出随网格数的增加,气动性能逐步趋于一个近似定常的值。在实际计算中,需要在计算花费和计算精度中间找到一个折中的网格数。
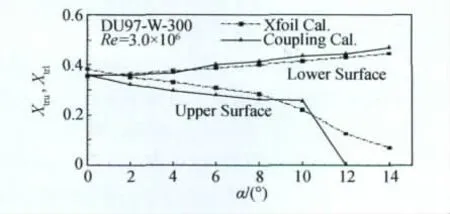
图6 转捩位置比较Fig.6 Comparison of transition locations
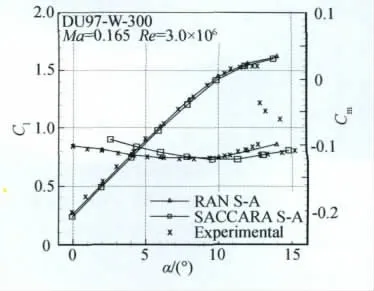
图7 升力系数和力矩系数比较Fig.7 Comparison of lift and moment coefficient
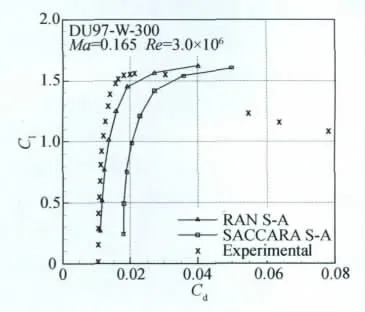
图8 极曲线比较Fig.8 Comparison of drag polar
(2)本文发展的耦合方法和考虑了时均效应的转捩模型可以用于钝后缘翼型的气动性能计算中,在10次转捩位置迭代之内可以得到收敛的转捩位置并得到翼型的气动性能。
(3)通过本文计算的气动性能和实验结果以及文献结果的比较,表明本文的耦合求解方法可以通过远少于参考文献的网格数得到和实验结果吻合更好的计算结果,但是失速迎角和最大升力系数的捕捉不好,还需要进一步的改进。阻力和力矩的计算结果也和实验值吻合较好,为此类翼型的设计和使用提供了数值模拟基础。
[1]MARSHALL L.Usage advice[EB/OL].http://wind.nrel.gov/designcodes/advice.html,Last modified 05-July-2005;accessed 28-Janu.-2010.
[2]PATRICK J.AeroDyn theory manual[R].NREL/EL-500-36881,2005.
[3]SIMMS D,SCHRECK S,HAND M,FINGERSH L J.NREL unsteady aerodynamics experiment in the NASA-Ames wind tunnel:A comparison of predictions to measurements[R].NREL/TP-500-29494.Golden,CO:National Renewable Energy Laboratory,2001.
[4]TANGLER J L.The nebulous art of using wind-tunnel airfoil data for predicting rotor performance[R].NREL/CP-500-31243.Golden,CO:National Renewable Energy Laboratory,2002.
[5]TPI Composites.Innovative design approaches for large wind turbine blades[R].SAND2003-0723,2003.
[6]TPI Composites.Innovative design approaches for large wind turbine blades-final report[R],SAND2004-0074,2004.
[7]STANDISH K J,van DAM C P.Aerodynamic analysis of blunt trailing edge airfoils[J].Journal of Solar Energy Engineering,2003,125(4):479-487.
[8]JACKSON K,ZUTECK M,van DAM C P,STANDISH K J,BERRY D.Innovative design approaches for large wind turbine blades[J].Wind Energy,2005,8(2):141-171.
[9]Van ROOIJ R P J O M,TIMMER W A.Roughness sensitivity considerations for thick rotor blade airfoils[J].Journal of Solar Energy Engineering,2003,125(4):468-478.
[10]BAKER J,MAYDA E,van DAM C P.Computational and experimental analysis of thick fatback wind turbine airfoils[R].AIAA Paper 2006-193,2006.
[11]CHAO D D,van DAM C P.RaNS analysis of an inboard flatback modification on the NREL phase VI rotor[R].AIAA Paper 2006-195,2006.
[12]WINNEMOLLER T,van DAM C P.Design and numerical optimization of thick airfoils[R].AIAA 2006-238,2006.
[13]TPI Composites.Computational design and analysis of flatback airfoil wind tunnel experiment[R].SAND 2008-1782,2008.
[14]STONE C,BARONE M,LYNCH C E,et al.A computational study of the aerodynamics and aeroacoustics of a flatback airfoil using hybrid RANS-LES[R],AIAA 2009-273,2009.
[15]刘雄,陈严,叶枝全.增加风力机叶片翼型后缘厚度对气动性能的影响[J].太阳能学报,2007,27(5):489-495.
[16]李秋悦,申振华.翼型进行钝后缘修改后气动性能的数值研究[J].沈阳航空工业学院学报,2007,24(1):1-5.
[17]张磊,杨科,赵晓路,等.不同后缘改型方式对风力机钝后缘翼型气动性能的影响[J].工程热物理学报,2009,30(5):773-776.
[18]HANS W S,HASSE W.Navier-Stokes airfoil computations with transition prediction including transitional flow regions[J].AIAA Journal,2000:38(11):2059-2066.
[19]MATTHEW F B,DALE B.Aerodynamic and aeroacoustic properties of a flatback airfoil:an update[R].AIAA Paper 2009-271,2009.
[20]STANDISH K J,van DAM C P.Analysis of blunt trailing edge airfoils[R].AIAA 2003-353,2003.
[21]KRUMBEIN A.Navier-Stokes airfoil computation with automatic transition prediction using the DLR TAU Code-A sensitivity study[M].New Results in Numerical and Experimental Fluid Mechanics V.,Springer Berlin/Heidelberg,Vol.92,2006.
[22]Der LEE J,JAMESON A.Natural-laminar-flow airfoil and wing design by adjoint method and automatic transition prediction[R].AIAA 2009-897,2009.
[23]TIMMER W A,van ROOIJ R P J O M.Design and wind tunnel test of airfoil DU 97-W-300[R].IW-98003R,Institute for Wind Energy,the Netherlands:Delft University of Technology,1999.

