几乎临界增长的方程外部 Dirichlet问题解的存在性

郭竹梅

(安徽科技学院 理学院, 安徽 凤阳, 233100)

几乎临界增长的方程外部 Dirichlet问题解的存在性

郭竹梅

(安徽科技学院 理学院, 安徽 凤阳, 233100)

讨论了一类几乎临界增长的半线性椭圆方程, 运用变分法和 Hardy 不等式得出了该类方程在外部区域上存在非平凡解.

临界增长; 变分法; Hardy 不等式; 非平凡解

本文研究如下几乎临界增长的半线性椭圆方程外部区域上解的存在性:

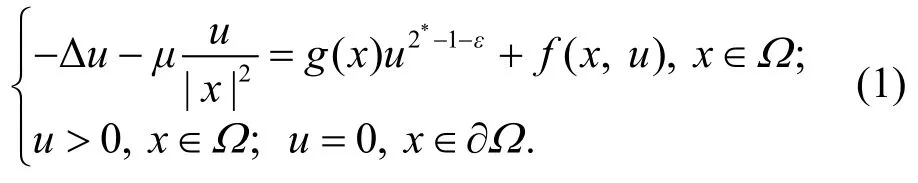
对于半线性椭圆方程, 其内部区域上解的存在性问题已被广泛地研究[1−7]. 文献[6−7]研究的都是内部区域上几乎临界增长的方程解的存在性问题,当 Ω为外部区域时, 近几年也有学者做了研究[8].本文采用变分法和 Hardy 不等式来研究方程(1)解的存在性, 研究的区域和方法与文献[6−7]不同, 且对文献[6−7]方程中给定的函数进行了推广, 即给定的函数推广为某一类函数时, 仍然能得到解的存在性,因而有一定的研究意义. 为了简单起见, 我们用“ → ”表示在相应空间中的强收敛, 用“”表示弱收敛.

1 预备知识

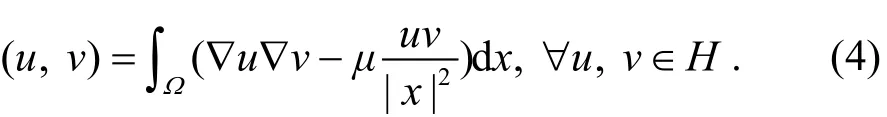
在本文中 u 是方程(1)的解, u∈H, 且对于任一 v∈

H 都成立:

方程(1)所对应的能量泛函为:

记I′( u )为 I( u )对应的 Fréchet导数, ∀v ∈H,

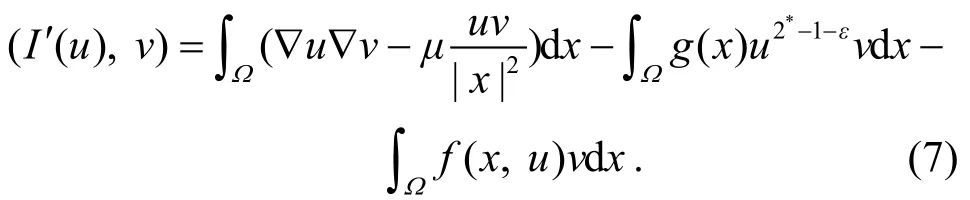
由变分法的主要思想可知, 若 u 是I( u )的临界点,即I′( u )=0, 则 u 必是方程(1)的解.

一般情况下选用P>0.05，P<0.05或P<0.01 3种方式表达，无须细分为P<0.001或P<0.0001。当P<0.05或P<0.01，均写为组间比较差异有统计学意义，并写明所用统计分析方法的具体名称，统计量的具体值。如成组设计资料的t检验、方差分析、q检验等。统计量的具体值，如t=2.10，F=8.78等。涉及到具体参数时给出95%可信区间。文中“差异有显著性”“差异无显著性”等均写为“差异有统计学意义”“差异无统计学意义”。差异有统计学意义时，其后标明P值，差异无统计学意义则不写P值。标准写法：差异有统计学意义(P<0.05或P<0.01)；P<0.05为差异有统计学意义。

2 主要结论

在得出主要的结论之前, 需要以下引理.

引理 1[8]设 Ω是如上所述的外部区域, 0 ≤, 则:

a. 存在常数C ＞0, 使得对任意 u∈H都有:

b. 若2*, 则嵌入 H Lq(Ω,是紧的.

引理 2[9](山路引理)设 X 是实 Banach 空间, I∈C1(X, R), 且I(0)=0, 假设:

证明 由(f2)得:

由式(9), (f3)得:

由(f3) 知, 当 u≥r时 , 有对u在即当 u≥r时,有: [r, u ]上积分得:

同理, 当 u≤ − r时, 有:

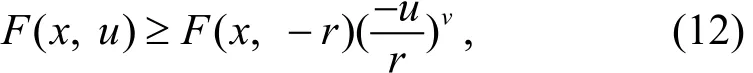
由式(11)、(12)可得, 当 |u|≥r时, 有:

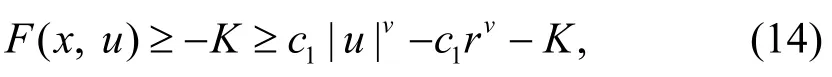
由式(13)、(14)易得:

下面验证泛函 I满足山路引理的条件.

a. 一方面, 显然I(0)=0, 由式(10)得, F( x,, 则:

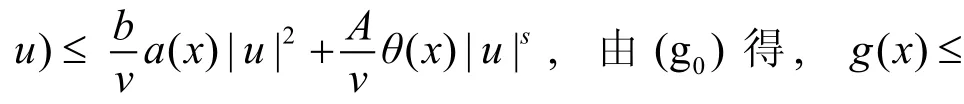
b. 另一方面, 对于任意 u∈H及t＞0,

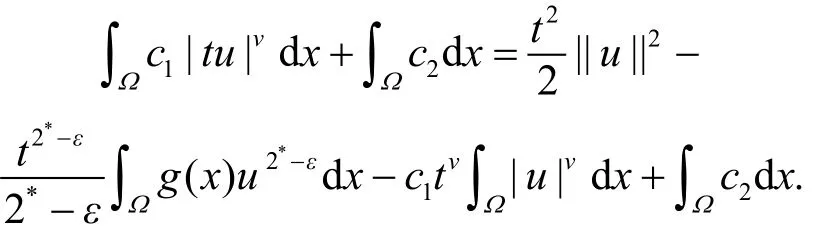
现取一个满足 ||u||=1的 u∈H, 由于2*−ε≥ ν＞2, 所以当 t→ +∞ 时, 有 I( tu )→ −∞ , 因此存在t＞ρ使得I( tu )≤0. 即存在e=tu∈H, ||e||=t＞ρ满足I( e) ≤0.

定 义Γ={γ∈C([0, 1], H); γ(0)=0, γ(1)=e},则由引理 2 得, c≥β＞0, 且 I关于 c 有临界序列. 即存在{un}⊂H s.t. I( un)→ c, I′( un)→0.

c. 最后验证 I 满足 P.S 条件, 由 I( un)=c+

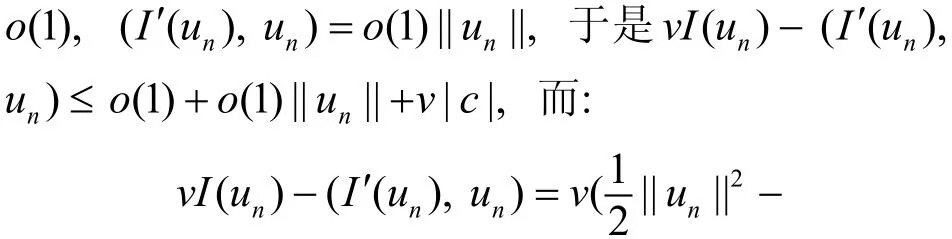
所以:

即:

即{un}在 H 中有界, 从而存在某个 u∈H, 使得在H 中有 un, 对任意的有界域U ⊂ Ω, {un}有子列(仍记为{un})满足un→u在La( U)中, 2≤a＜

2*. 又因为:

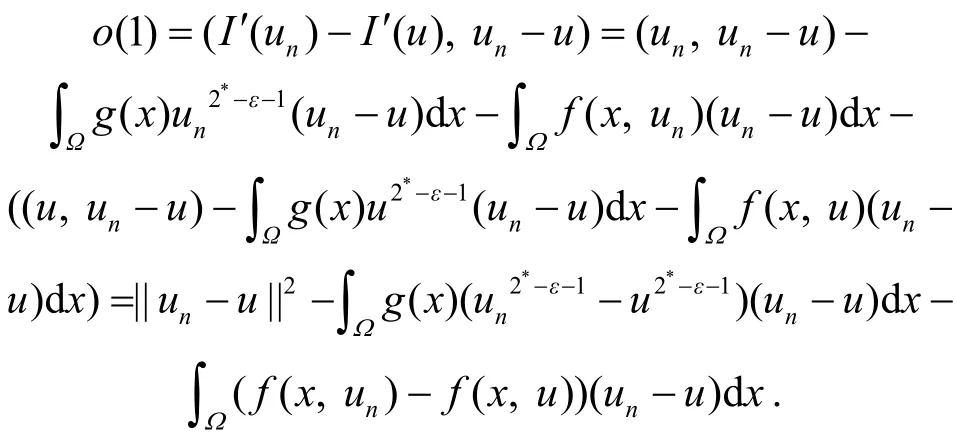
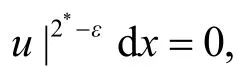
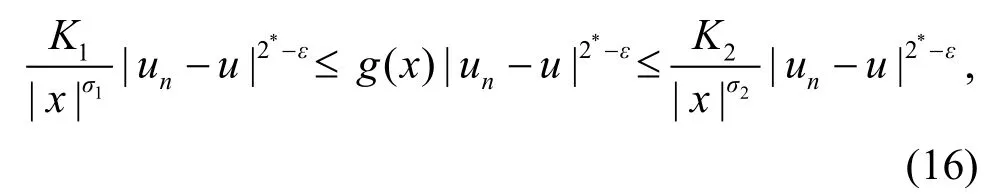
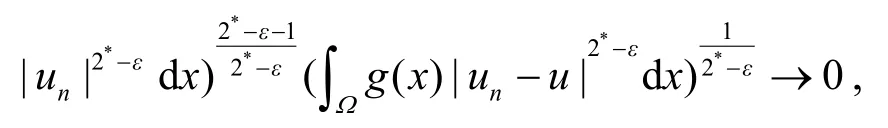
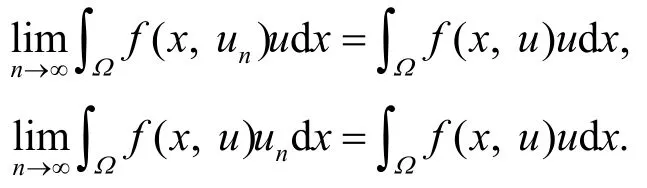
[1] Jannelli E. The role played by space dimension in elliptic critical problems[J]. J Diff Eq, 1999, 156(2): 407−426.

[2] Carcia J, Peral I. Hardy inequalities and some critical elliptic and parabolic problems[J]. J Diff Eq, 1998, 144(2): 441−476.

[3] Ghoussoub N, Yuan C. Multiple solutions for quasi−linear PDES involving the critical Sobolev−Hardy exponents[J]. Trans Amer Math Soc, 2000, 352(12): 5703−5743.

[4] Cheng Ting. Existence of minimal positive solution for[J]. Journal of Central China Normal University: Natural Science, 2001, 35(2): 136−140.

[5] Kang Dongsheng, Deng Yinbing. Existence of solution for a singular critical elliptic equation[J]. J Math Anal Appl, 2003, 284(2): 724−732.

[6] 姚仰新, 许金泉, 姚若河. 几乎临界增长的半线性椭圆方程正解的存在性[J]. 数学物理学报 , 2000, 20(4): 487− 492.

[7] 易刚. 一类几乎临界增长方程解的存在性[J]. 湖北汽车工业学院学报, 2009, 23(4): 53−55.

[8] 康东升, 朱小琨. 外部区域上半线性椭圆方程的多解[J]. 华中师范大学学报: 自然科学版, 2003, 37(1): 3−5.

[9] 陆文端. 微分方程中的变分方法[M]. 北京: 科学出版社, 2003: 254−255.

(责任编校: 刘晓霞)

Existence of solution for the exterior dirichlet problems involving the equation with nearly critical exponent

GUO Zhu−mei
(Institute of Science, Anhui Science and Technology University, Fengyang 233100, China)

Using variational methods and Hardy inequality, the existence of nontrivial solution to a kind of semilinear elliptic equation with nearly critical exponent is given.

critical exponent; variational methods; Hardy inequality; nontrivial solution

O 175. 2

1672−6146(2011)02−0009−04

10.3969/j.issn.1672−6146.2011.02.003

2011−03−30

安徽科技学院校级课题(ZRC2008194)

郭竹梅(1980−), 女, 助教, 硕士, 研究方向为偏微分方程及其应用. E−mail: zhumei.guo@163.com