一类捕食与被捕食系统的正解与持久性

曾华东, 马满军, 曾繁盛

(1. 南华大学 数理学院, 湖南 衡阳, 421001; 2. 江西省兴国县梅窖中学, 江西 赣州, 342432)

一类捕食与被捕食系统的正解与持久性

曾华东1,2, 马满军1, 曾繁盛2

(1. 南华大学 数理学院, 湖南 衡阳, 421001; 2. 江西省兴国县梅窖中学, 江西 赣州, 342432)

利用泛函微分方程正解的比较原理、上下极限原理及分析技巧, 研究了一类具 Beddington−DeAngelis 型功能反应的捕食−被捕食系统, 获得该系统正解的存在性以及该系统持久性的充分条件.

比较原理; Beddington−DeAngelis 型功能反应; 持久性

本文考虑具 Beddington−DeAngelis 功能反应的捕食与被捕食系统:

获得了该系统持久性的充分条件.

定义 1如果存在正常数 M 和 ε使得系统(1)的所有正解满足条件:

则称系统(1)是持久的.

引理 1若x(0)、y(0)＞0, 则系统(1)的解x( t) 、y( t) 在 (0, ∞ )上存在且恒大于 0.

证明由系统(1)的第 1 个方程有:可得, 因为x(0)＞0, 所以有x( t) ＞0, t∈(0, ∞).

下证y( t) ＞0. 反设在 (0, ∞ )中有使得y( t)=0的点, 且设. 由y(0)＞0知y′( t0)≤ 0.

b. 若 t0∈(τ, 2τ], 则由 a.可知y( t0−τ)＞0, 结合()0x t ＞, 有这也与y′( t0)≤0矛盾. 所以 t0∉(τ, 2τ], 即y( t) ＞0,

重复以上的证明, 可推得y( t) ＞0, t∈(0, ∞).

由上述证明可知系统(1)的解(0)x、()y t 在 (0,∞ )上存在且恒大于 0. 证毕.

由文献[1]可得引理 2−4.

引理 2 系统(1)的解有最终上界, 即:

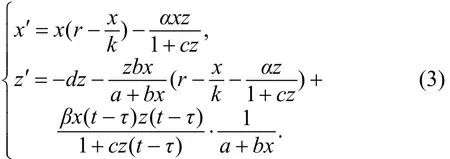
显然, 系统(3)和(1)正解的持久性等价. 为了获得系统(1)的持久性条件, 先考虑系统(3)正解的最终有界性.

定理 1 系统(3)的正解是有最终上界的.

证明 由引理 2, 只需证明正解的 2 个分量有最终下界即可. 定义函数:

我们可以选择充分小的0ε＞和10ε＞, 使得:

断言 1 不可能存在充分大的0t, 使得当0tt＞时, ()x tε＜.

证明 反设存在充分大的0t 使得: 当0tt≥时,有()x t ＜ ε, 则进而有()x t ＞因

此可推得:

考虑方程:

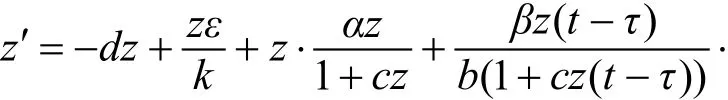
由文献[2]知, 方程(6)的正解关于初值是单调的. 由式(4)容易验证zM(ε)是式(6)的最大非负平衡解, 且当z＞zM(ε)时, f( z, ε)＜0. 定义φ ( θ)=nk, θ∈0[−τ, 0], 其中n ＞1充分大, 使得zM(ε)＜nk. 因此, f( nk, ε)＜0. 如果z( t, t0, φ0)表示式(6)经过点(t0, φ0)的解. 由 文献[3−4]知, 当 t→ +∞ 时, z( t, t0, φ)→zM(ε). 由比较原理[2], 当 t充分大时, 有0 z( t)＜zM(ε)+ε. 结合式(5), 可得:

显然, 当 t→ +∞ 时, x( t) → +∞. 这与反设矛盾. 因此断言 1 正确.

我们可以选择充分大的 T1＞0, 使得z( T1, 0,这里是式(6)过(0, φ0)的解. 下面将证明: 对充分大的 t, 有:

反设式(7)不成立, 结合断言 1, 存在充分大的 t1和且满足x( t1)=ε,当时, 有且x′( t) ≤0.

由系统(3)的第 1 个方程有:

由此, 可得:

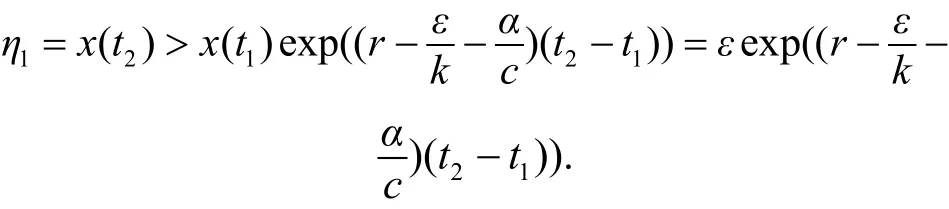
由已知条件显然有 t2−t1＞T1. 重复断言 1 的证明, 可推得因此, 有:

这与x′( t) ≤0矛盾. 因此式(7)成立. 注意到正常数η1不依赖于正解的选择. 因此 η1是系统(3)正解第1 个分量x( t) 的最终下界.

下面证明系统(3)正解的第 2 个分量 z( t) 存在最终下界.

选择 ε2充分小, 以满足kr＞ε2＞0, 且使得下式成立:

断言 2 不可能存在充分大的 t3, 使得当t＞t3时, 有

证明 反设断言 2 不成立, 即存在 t3, 使得:

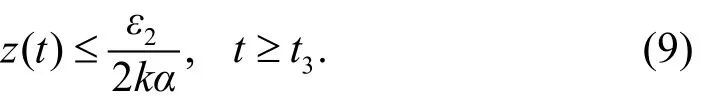
由系统(3)的第 2 个方程及式(10), 有:

考虑方程:

由于式(11)的正解关于初值是单调的[2], 易验证当t→ +∞ 时, 式(11)的正解趋于:

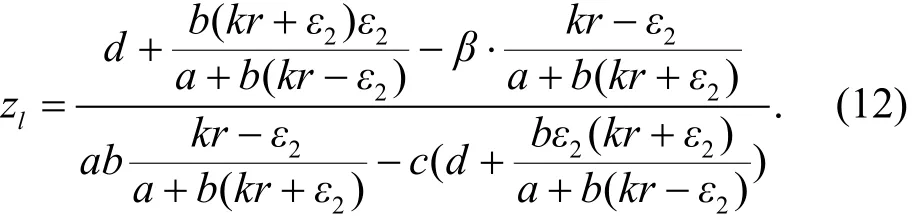
因为式(7)成立, 为了叙述简单, 以下过程中总假设对所有t≥0, 有x( t)≥η1.

考虑方程:

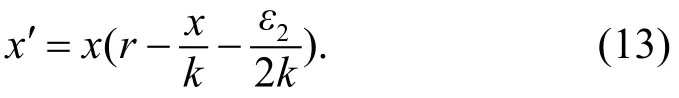
设x( t, η1)是式(13)过(0, η1)的解, 则可以选择充分大的 T3, 使得:

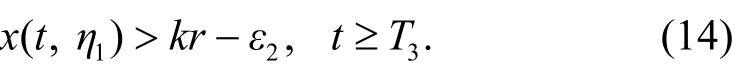
假设式(15)不成立, 则由上面的讨论知, 存在 t4＜ t5＜t6, 使得时,

由系统(3)的第 2 个方程, 可得z′( t) ≥−dz −我们有由此及式(14)和比较原 理[2], 有x( t)＞kr−ε2, ∀t ∈[t4+ T3, t6). 由此, 可得:且让z( t,t5, φ) 表示

令当t＞t5时, z( t, t5, φ) 是单调递增的. 结果由比较原理[2], 当 t5＜t＜t6时,这与假设: 当矛盾. 因此系统(3)成立. 所以系统(3)的第 2 个分量以 η2为最小下界. 因此系统(3)是持久的. 定理 2 证毕.

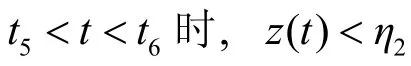
推论 1 如果下面的假设(H)成立, 且以下条件之一正确:则系统(15)是持久的.

定理2及推论1表明捕食者之间的相互作用影响系统的持久性.

[1] Wang W, Mulone G, Salemi F, et al. Permanence and stability of a stage−structured predator−prey model[J]. J Math Anal Appl, 2001, 262: 499−528.

[2] Smith H L. Monotone semiflows generated by functional differential equations[J]. J Differential Equations, 1987, 66: 420−422.

[3] Holt R D. Population dynamics in two path environment: Some anomalous consequences of optional habitat selection[J]. Theoret Popul Biol, 1985, 28: 181−208.

[4] Smith H L. Monotone Dynamical Systems: An Introduc−tion to the Theory of Competitive and Cooperative Systems[J]. Math Surveys Monographs, 1995, 41: 30−32.

(责任编校: 刘晓霞)

Positive solutions and permanence of a class of predator−prey system

ZENG Hua−dong1,2, MA Man−jun1, ZENG Fan−sheng2
(1. School of Mathematics and Physics, University of South China, Hengyang 421001, China; 2. Meijiao Middle School, Ganzhou 342432, China)

This paper studied a class of predator−prey models with Beddington−DeAngelis functional response by applying the comparison principle for positive solutions of functional differential equations, supper and lower limit principle and analytical techniques. Existence of positive solutions and sufficient conditions for the permanence of this system are obtained.

comparison principles; Beddington−DeAngelis functional response; permanence

O 175

1672−6146(2011)02−0001−04

10.3969/j.issn.1672−6146.2011.02.001

2011−05−13

曾华东(1977−), 男, 硕士研究生, 研究方向为微分方程与动力系统. E−mail: zenghuadong1977@163.com