柯西不等式证明及应用
黄卫
(南京晓庄学院,江苏 南京 211171)
柯西不等式证明及应用
黄卫
(南京晓庄学院,江苏 南京 211171)
本文探讨了柯西不等式多种证明方法,通过一系列的例题,反映了柯西不等式在函数求最值及其在几何上(距离)的广泛应用.
柯西不等式;证明;应用
柯西不等式是由大数学家柯西(C a u c h y)在研究数学分析中的“流数”问题时得到的.但从历史的角度讲,该不等式应当称为 C a u c h y-B u n i a k o w s h y-S c h w a r不等式.正因为是后两位数学家彼此独立地在积分学中推而广之,才将这一不等式应用到近乎完善的地步.
在我国的一般高校教育中,微积分、线性代数和概率论是最基本的数学基础课程.表面上看,这三门课存在很大差异,但与此同时它们却往往可以从不同的角度和方法对同一事物作出证明及解释.著名的柯西不等式在不同领域中的证明方式充分说明了人们思维的多样性、渗透性和完备性.认识这一点可以使思维更活跃,也可以使我们的学习更富有创造性.
1 柯西不等式及其证明
1.1 柯西不等式
柯西不等式拥有多种形式,下面是其几种形式.
二维形式:(a2+b2)(c2+d2)≥(a c+b d)2等号成立条件:a d=b c
向 量 形 式 :|α ||β |≥|α·β|,α=(a1,a2,… ,an),β=(b1,b2,… ,bn)(n∈N,n≥2)等号成立条件:β 为零向量,或 α=λβ(λ∈R).
1.2 下面给出柯西不等式的证明
证明 1(直接法)
则
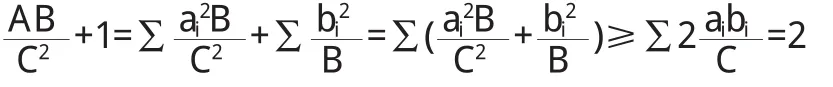
证明 2(利用二次型)

即关于 x、y的二次型非负定,那么

证明 3(数学归纳法)
当 n=k+1时
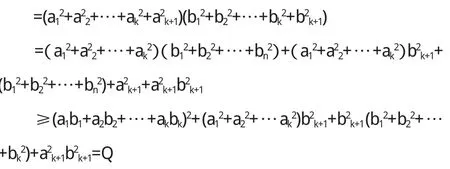

即 n=k-1时,不等式成立
综上所述,得对对 n∈N+,不等式成立,故得证.
证明 4(利用线性相关证明)
经过仔细探讨发现,为了严格而简洁地刻划出(a1,a2,…, an)与(b1,b2,…,bn)具有什么 关系 时才成为柯 西不 等式 中等号成立的充要条件,我们从向量线性相关、线性无关的概念出发,来叙述并证明这种特殊的柯西不等式.设 Rn为向量空间.
当且仅当向量ζ与η线性相关时,

证明
(ⅰ)设 ζ、η 线性相关,则存在不全为 0的 k、1∈Rn,使k ζ+l η=0
无论何种情形代入柯西不等式两端便知等号成立.
(ⅱ)设 ζ、η 线性无关,则对每个 x∈R.有 ζ-x η≠0,即至少有一个 i,1:i:n使 ai-bix≠0于是
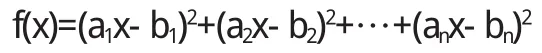
或

这里 η≠0,否则 ζ、η 线性相关与题设矛盾.
于是有 b1,b2,…,bn不全为 0和这样推出△<0
即
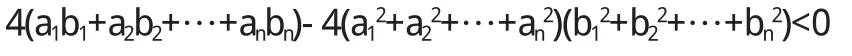
于是

(ⅲ)若柯西不等式等号成立.则 ζ、η 必线性相关.不然由(ⅱ)将推出柯西不等式等号不成立.证毕.
以上严格的命题叙述和证明,是把高等代数对一般抽象欧氏空间相应命题及其证明改写为特殊形式.
3 柯西不等式的应用
例1(距离问题)
利 用 柯 西 不 等 式 证 明 : 平 面 点 p(x0,y0)到 直 线A x-B y-C=0的距离公式

证明 对直线上的任意一点 Q(x,y),得 A x-B y=-C,且A2-B2>0
由柯西不等式,得
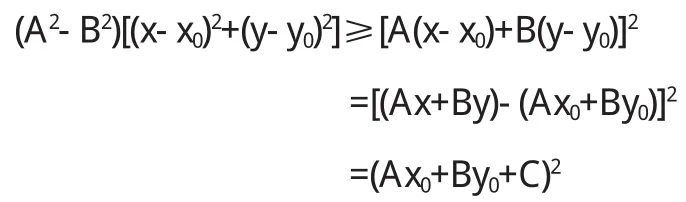
则,有
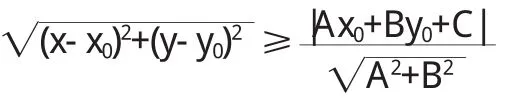
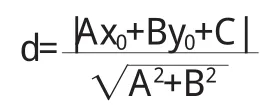
以上证明运用的背景均在二维平面内,由此可以考虑发展到三维空间点到面的距离公式,在 n维抽象空间中,球点到空间中任意点的距离最小,这就是极值的问题.
例2(极值问题)
如果 x1+…+xn=1,a>0,那么当且仅当 a1x1=…=anxn时,f(x)的最小值是

以上证明的是一个极值问题,是在 x1-x2-…-xn=1的条件下成立.如果把此条件推广成,求 f(x) =x1+x2+…+xn的最大值,一样能够求得.
上面我们介绍了柯西不等式及各种形式,并证明了一般形式,在此基础上并阐述了它的一些应用.
〔1〕徐 幼 明.柯西不 等 式的推广 及 其应用[J].数 学 通 讯 ,1996(12):25-26.
〔2〕王莲花,李晔,李战国,刘芳.柯西不等式的证明及应用研究[J].河南教育学报,2003,12(1):5-7.
〔3〕王玉兰.柯西不等式的一个简单证明及其应用[J].内蒙古科技与经济,2002(8):135.
〔4〕刘 治 和 .浅 谈 柯 西 不 等 式 的 证 明 及 应 用 [J].数 学 通 报 ,2000,18(5):44-46.
〔5〕 方海燕. 柯西不等式的应用 [J]. 数理天地 (高中版),2005,13(10):21-23.
O 1 7
A
1673-260X(2011)04-0015-02

