R L S自适应滤波器的 M a t l a b设计与仿真
张立萍
(赤峰学院 物理与电子信息工程系,内蒙古 赤峰 024000)
R L S自适应滤波器的 M a t l a b设计与仿真
张立萍
(赤峰学院 物理与电子信息工程系,内蒙古 赤峰 024000)
自适应滤波技术已经被广泛应用于数字通信、雷达、生物医学和工业控制等领域.本文介绍了 RLS 算法,并以随机干扰噪声信号为研究对象,在 Matlab 上设计了 RLS 自适应滤波器的 M 文件,进行了仿真,为硬件实现提供了有力的参考.
自适应滤波器;RLS 算法;Matlab;M 文件
1 引言
目前,自适应滤波器技术在通信和雷达技术的信道均衡、回波抵消、噪声消除或抑制、语音编码、自适应跳频、天线旁瓣抑制、谱线增强、雷达杂波处理、雷达运动目标显示、窄带干扰抑制以及生物医学中的微弱电信号的处理等方面均获得了广泛的应用.自适应滤波器是这样的处理器,它在输入信号特性未知或者输入信号特性变化时,能够调整自己的参数,以满足某种最佳滤波准则的要求.
在设计滤波器时应该根据输入信号的特性,设计出最佳的滤波器.那么,什么样的滤波效果才算是最佳呢?必须有一个判断的标准.至今已研究出很多最佳滤波准则.常见的有最小均方误差准则、最小二乘准则等.最佳滤波准则和自适应滤波器关系密切,最佳滤波准则规定了与某种特性的信号对应的最佳参数,而这个最佳参数指出了自适应滤波器调整参数的方向.以下主要介绍这两个准则.
(1)最小均方误差准则 L M S(L e a s tM e a nS q u a r e)就是要使输出信号和理想信号的误差的平方的均值最小.设 d(n)为滤波器输出要逼近的信号,y(n)为滤波器输出信号,则误差为 e(n)=d(n)-y(n),最小均方误差准则就是要使 E{e2(n)}达到最小.
(2)最小二乘准则 L S(L e a s t S q u a r e)就是要使一定范围内(从 k到 k+m-)误差的平方和达到最小,也就是要使达到最小.
2 最小二乘法(RLS)
最 小 二 乘 算 法(L S,L e a s t-s q u a r e s)是 一 种 批 处 理 方 法 ,通过一个数据块接一个数据块的重复计算来适应非平稳数据,因此它的计算量大.推广最小二乘法将得到一种应用更广泛的算法,即递推最小二乘法(R L S).一般说来,R L S算法具有较好的收敛性能和跟踪能力,但是要求较多的计算量,目前最快的 R L S算法要比 L M S算法多 2-3倍的计算量,因此,R L S自适应滤波一般用于要求较高的场合.
2.1 R L S算法原理
由于 L M S算法的收敛速度很慢,为了得到较快的收敛速度,有必要设计包含附加参数的更复杂的算法.在快速收敛算法的推导中,我们将采用最小二乘法.因此,将直接处理接收数据,使二次性能指数最小,而 L M S是使平方误差的期望值最小.这就意味着用时间平均而不是统计平均来表示性能指数.
基于时间平均的最小平方误差被定义如下:

式中,λ 是接近 1,但是小于 1的加权因子,且误差 e(i)为:


式中,X(i)是 i时刻的输入数据向量,W(n)是 n时刻的新的抽头增益向量.因而 e(i)是用 n时刻的抽头增益向量测试时刻的旧数据所得的误差,J(n)是在所有旧数据上用新抽头增益所得的累计平方误差.
要完 成 R L S算法 就 要 找到均 衡 器 的 抽 头 增 益 向 量 W (n),使得累计平方误差 J(n)最小.为了测试新的抽头增益向量,会用到那些先前的数据.而因子 λ 会在计算时更依赖于新近的数据,也就是说,J(n)会丢掉非稳定环境中的较旧的数据.如果信道是稳定的,那么 λ 可以设为 1.
为了获得 J(n)的最小值,可使 J(n)的梯度为 0,即(n)=0通过运算可知:



要用式(4)均衡器的抽头增益向量W^(n),就需要计算 R-1(n).从式(5)中 R(n)的定义式,我们可以得到关于 R(n-1)的递归公式:

同理得到 P(n)的递推表示式为:

根据矩阵求逆定理,若 A,B是 M×M的正定矩阵,C是一个 M×N矩阵,D是一个 N×N矩阵,当 A=B-1+C D-1CT时,有 A-=B-B C(D+CTB C)-1CTB.现 令 A=R(n),B-1=λR(n-1),C=X(n),D=J,可以得到 R-1(n)递归公式:

则(9)变为:

将式(1 0)中 K(n)的表示式重新安排:
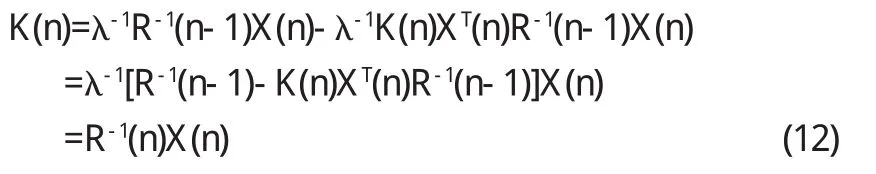
由式(4)、(8)、(1 1)和式(1 2)可得W^(n)的递推公式:

2.2 R L S算法实现
②对于每一个时刻 n=1,2,…,进行如下计算:

这样,就用 R-1(n)的递归运算来取代了矩阵反演运算[XT(n)X(n)]-1.其中,δ 是正则化参数,δ 的设定与信噪比有关,正 则化 参数 δ 与 信噪比 的关 系己 由 M o u s t a-k i d e s(1 9 9 7)给出详细说明.
3 RLS 自适应滤波器 M 文件的设计与仿真
根据前面介绍的 R L S算法,用 M A T L A B设计 R L S自适应滤波器.下面将在 M A T L A B环境中编写 M文件对 R L S算法进行设计和仿真,验证算法的可行性.
在 M A T L A B中编写 M 文件 R L S.m,其中,各参数的意义如下:
s:标准正弦信号,最大峰值为 m a x V p=1.0 0. s
n:标准信号叠加标准白噪声(最大峰值为 m a x V p=3.9 4). s
t e p:滤波器指数加权因子 λ,取值为 0.9 9.
W(n):滤波器的权向量序列. e
n:s(i)信号减去滤波器输出信号后得到的误差信号.
N:时域抽头 R L S算法滤波器阶数,取值为 1 2 8.
d l e n:输入信号抽样点数,取值为 1 0 2 4.
d e l t a:正则化参数 δ,取值为 0.0 0 1.
R L S算法中各向量的更新表达式在 M文件中的实现代码为:

仿 真 时 ,原始信号选为 s i n((0.0 5*p i*t),其 中 t=1:d l e n,噪声信号采用标准白噪声,在 M A T L A B环境中运行 R L S.m文件,调用绘图函数,得到 R L S算法的仿真结果如图 1.R L S算法的均方误差曲线如图2所示.

图 1 R L S算法的输入和输出曲线

图 2 R L S算法的均方误差曲线
4 结束语
R L S算法具有良好的收敛速度,除收敛速度快于 L M S算法以及稳定性强外,而且具有更高的起始收敛速度、更小的权噪声和更大的抑噪能力.
〔1〕么 晖.基于 FPGA 的 自 适应 滤 波 器 设计[D].硕 士 学位 论文.北京:航天科工集团第三研究院,2005.
〔2〕黄埔堪,陈建文,楼生强.现代数字信号处理[M].北京:电子工业出版社,2003.
〔3〕龚耀寰.自适应滤波器[M].北京:电子工业出版社,1989.
〔4〕韩利竹.MATLAB 电子仿真与应用[M].北京:国防工业出版社,2001.
〔5〕王立宁,乐光新.MATLAB 与通信仿真[M].北京:人民邮电出版社,2000.
〔6〕Simon Haykin.Adaptive Filter Thearo[M].北 京 :电 子工 业出版社,2006.
T N 2 7 3.2
A
1673-260X(2011)04-0025-02

