接地导体薄圆筒与不共轴平行导体圆筒的电势和电场
范梦慧
(贵州民族学院 理学院,贵州 贵阳 550025)
接地导体薄圆筒与不共轴平行导体圆筒的电势和电场
范梦慧
(贵州民族学院 理学院,贵州 贵阳 550025)
利用复数坐标系上的保角变换,分两种情况讨论接地导体薄圆筒与不共轴平行导体圆筒之间的电势和电场的分布函数,所得两种函数表达形式相似.
保角变换;接地导体薄圆筒;平行导体圆筒;电势分布;电场分布
在 教 材 中[1,2,3],通 常 以 两 无 限 长 共 轴 圆 筒 为 例 利 用 高 斯定理和电势定义式计算其电场和电势的分布,然而对于两不共轴无限长圆筒直接用教材中的方法很难得到其电场分布.本文分接地无限长导体薄圆筒与筒外无限长平行导体圆筒及接地无限长导体薄圆筒与筒内不共轴的无限长平行导体圆筒两种情况,运用保角变换法[4]把不共轴的两圆筒变换为共轴两圆筒直接由无限长圆筒外的电势直接算出其电势和电场分布函数.
1 接地导体薄圆筒与筒外平行导体圆筒的电势与电场分布
半径为 a,单位长度上电荷为 q的无限长圆筒 C 1与筒外半径为 b接地无限长导体薄圆筒 C 2平行,两轴相距为 d(d>a+b).因在垂直于两圆筒轴线的所有平面上电场的分布均相同,所求的电场为平行平面场,可取任一截面为复平面z,以导体薄圆筒 C 1的圆心为原点,以两轴的连线为 y轴建立坐标系如图1所示,讨论其电势和电场在该复平面上的分布.为了简便地求出电势的分布,利用保角变换可将 C 1和 C 2变 为 同 心 圆 ,在 z平 面 上 选 点 A(0,i y1)和 点 B(0,i y2),两点关于圆 C 1和圆 C 2均对称,y1和 y2所要满足的方程组如下

解方程组(1)得
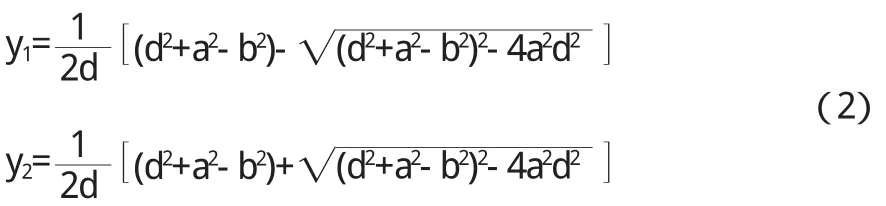
设所求的变换为分式线性变换

图 1 z平面上两圆筒的截面(d>a+b)

通过变换把 z平面的 A点变为 ζ平面的原点 ζ=0,把点B变为 ζ平面的无限远点 ζ=∞.圆 C1变为 ζ平面上以原点ζ=0为圆心的圆 C1,圆 C2变为 ζ平面上也是以原点 ζ=为圆心的圆 C2(如图 2所示),这样圆 C1和 C2是同心圆.
为了计算同心圆 C1和 C2的半径 a和 b.在 z平面上的圆 C 1上取一点 z1=-a i,在圆 C 2上取一点 z2=(d+b)i,代入式(3)得

由于在保角变换后相应区域的总电荷量保持不变,则在ζ平面上,单位长度电荷为q的无限长圆筒外的电势直

图 2 ζ平面上的两圆筒的位置(d>a+b)
接写为

其中 k为实常数,其值可由圆 C2'为零点电势确定


把 k值代入式(5)得
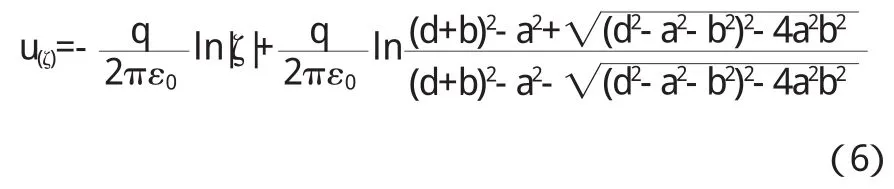
将 u(ζ)变回到 z平面 ,可得接 地无限长导 体薄圆筒与筒外无限长平行导体圆筒之间的电势分布函数为

z平面上接地无限长导体薄圆筒与筒外无限长平行导体圆筒之间各点的电场由E→=-▽u得:
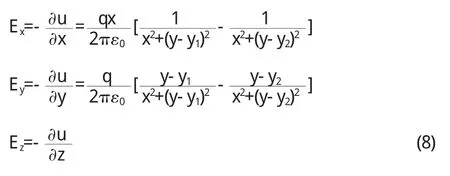
再将(2)式中 y1,y2值代入上式即可.
导体圆筒 C 1和 C 2内各点的电场由导体静电平衡条件得
圆筒 C 1是一等势体,其电势由式(4)和式(5)算出
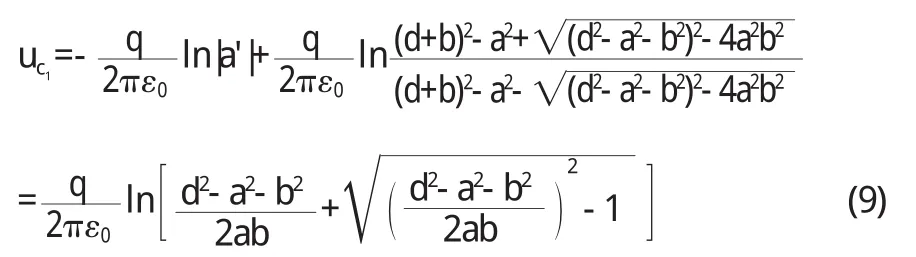
2 接地导体薄圆筒与筒内不共轴的平行导体圆筒的电势与电场分布
半径为 R1的接地无限长导体薄圆筒 G 1与筒内半径为R2单位长度上的电荷为 q的无限长导体圆筒 G 2,两轴平行,相 距为 D(D 图 3 z'平面上两圆筒的截面(D 为把 G 1和 G 2变为同心圆,在 z'平面上取与圆 G 1和圆G 2均对称的两点(0,i y1)和(0,i y2),则有方程组 解方程组(1 0) 同理,算出经保角变换后的同心圆 G 1'和 G2'的半径 R1'和R2'(R1'>R2',圆 G1'接地),图略. 在经保角变换后的ζ平面上接地两导体圆筒之间的电势写为 其中 k'为实常数,其值可由圆 G1'为零点电势确定 得 代入(1 3)式 将 u(ζ)变回到 z'平面,可得其电势分布函数为 z'平面上接地无限长导体薄圆筒与筒内不共轴的无限长平行导体圆筒之间各点的电场由E→=-▽u得: 再将(1 1)式中 y1,y2值代入上式即可. 圆筒 G2是一等势体,其电势由式(1 2)和式(1 4)算出 利用保角变换法把不共轴的两无限长圆筒变为共轴的两无限长圆筒,从而简便算出其电场与电势的分布函数.对于所讨论的上述两种情况,接地导体薄圆筒与不共轴的平行导体圆筒之间的电势与电场分布函数表达形式相似,只是参数不同.不共轴两平行导体圆筒之间的电场也可由镜像法求出,由于篇幅原因,本文不再进行阐述. 〔1〕赵 近 芳.大 学 物 理 学 (下)[M].北 京 :北京 邮 电 大 学 出 版社,2008:45-46. 〔2〕马文蔚.物理学(中)[M].北京:高等教育出版社,1999:54. 〔3〕张 三 慧.大 学 基 础 物 理 学 (下 )[M].北 京 :清 华 大 学 出 版社,2003:375. 〔4〕梁昆淼.数学物理方法[M].北京:高等教育出版社,1998:433-434. O 4 4 1.1 A 1673-260X(2011)04-0022-03






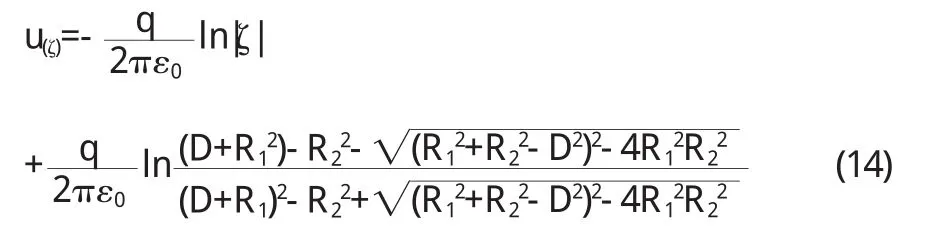
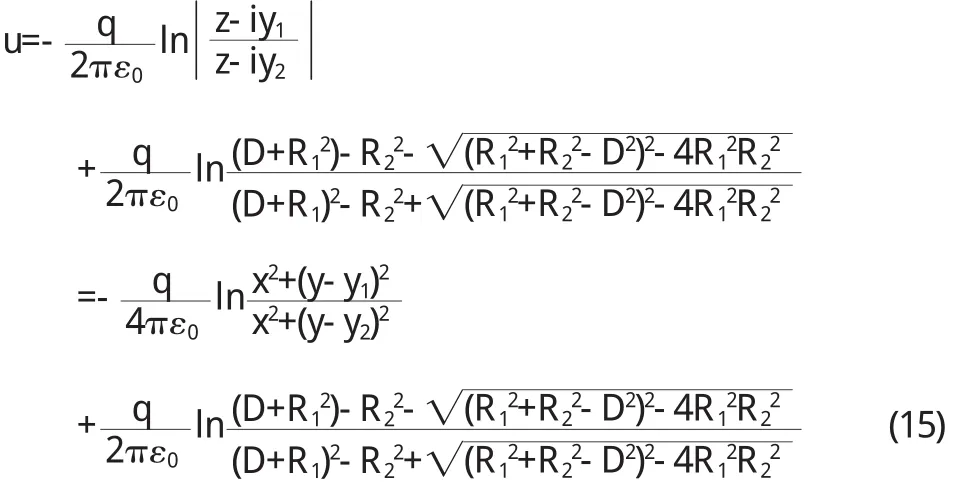

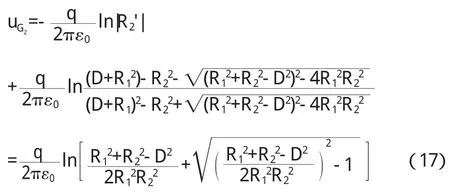
3 结束语

