G L(3,2)是 1 6 8阶不可解单群
孔亚峰
(1.曲阜师范大学 数学科学学院,山东 曲阜 273100;2.济宁学院,山东 曲阜 273100)
G L(3,2)是 1 6 8阶不可解单群
孔亚峰
(1.曲阜师范大学 数学科学学院,山东 曲阜 273100;2.济宁学院,山东 曲阜 273100)
为了更好的理解 GL(3,2)是 168 阶不可解单群,本文利用有限群论的有关知识,运用分类讨论的方法,给出了 GL(3,2)是 168 阶不可解单群一个新的证明.
有限群;单群;可解群
1 预备知识
我们用 K≥G表示 K为 G的正规子群,Gα表示α的稳定子群.所有群论术语及主要符号见文[1].
定义1 称有限群G为单群,如果G只有平凡正规子群.
定义2 如果G在Ω上只有一个轨道,即Ω本身,则称G在Ω上作用是传递的.
2 主要结果
定理 1(G L(3,2)是 1 6 8阶不可解单群.
证明 下面分四步证明:
(ⅰ)|G L(3,2)|=1 6 8.事实上,设 V为 Z2上的三维向量空间,G L(3,2)表示可逆线性变换的集合,基的个数为(23-1)(23-2)(23-22)=1 6 8,故 |G L(3,2)|=1 6 8.
(ⅱ)设 V*=V-1,令 G=G L(3,2),则 G在 V*上传递,即对任意的 α,β∈V*,存在 c∈G,使 ασ∈β.
(ⅲ)G L(3,2)不可解.反证法,设 G可解,N是 G的极小正规子群,则 N是 A b e l p-群,设 N=P1× P2× … Pm,由 N极 小 知 ,N=P为 p-群 , 令 H=},则 H c h a r N,存在H c h a r N≤G,H≤G,由 N的极小性知 H=N.G的极小正规子群 N是初等 A b e l p-群,这时 N在 V*上传递,事实上,V*=α1,α2,…,α7,Nαi表示 N中固定的元素 αi的集合,α1所在的轨道长为(N:Nαi).设 Nαi在 N中的陪集为为 α1所在的轨道,事实上彼此不等,若不然,若则矛盾,所以彼此不等,又,故对任意 g∈N,存在 gi使,任 意,存 在(3,2),使,事实上,α1g∈, 同 理 可 证把 G L(3,2)分 成 等 长 的 若 干 个 轨 道 , 由 于,若所以,因而 |N|=3或
(1)|N|=3,N是 G L(3,2)的正规子群,取 A=不正规 G,矛盾.
(2)|N|=2,N=〈a〉,任 意 g∈G=G L(3,2),g-1a g∈N,所以 g-1a g=a,a∈Z(G),G L(3,2)=1,矛盾.
(3)|N|=22=4,则 GG(N)的 S y l o w 2-子群可交换,盾.


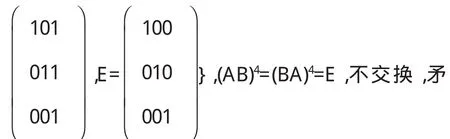
(4)|N|=23=8,这 时 G=G L(3,2)的 S y l o w 2-子 群正规且是一个 A b l e群,取且 A B≠B A,矛盾,所以不成立,所以 N在 V*上传递,|N:Nα1|=7,故 7||N|,所以|N|=7,G=G L(3,2)的 S y l o w 7-子群正规,由上已证矛盾,因而得到G不可解.
(ⅳ)G=G L(3,2)为单群,若不单,则存在 N≠1,G◁G,|N||23×7×3,N可解,G/N可解,从而 G可解,矛盾.故 G=G L(3,2)为单群.
综上所述,G L(3,2)是 1 6 8阶不可解单群.
〔1〕徐明曜.有限群导引(上、下册)[M].北京:科学出版社,2001.
O 1 5 2.1
A
1673-260X(2011)05-0009-02

