用射影几何构作新的A2-码
张晓寒,王文贤
(1.衡水职业技术学院基础部,河北衡水 053000;2.河北师范大学数学与信息科学学院,河北石家庄 050016)
用射影几何构作新的A2-码
张晓寒1,王文贤2
(1.衡水职业技术学院基础部,河北衡水 053000;2.河北师范大学数学与信息科学学院,河北石家庄 050016)
利用射影几何构作了一个新的带仲裁的认证码,并计算了它的参数。进一步假设全部规则是按等概率分布选择的,分别计算了5种攻击成功的概率。
认证码;带仲裁的认证码;射影几何
为了防止发方与收方之间的相互欺骗,SIMMONS在普通认证码的基础上引入了带仲裁的认证码模型(简记为A2-码)[1],此模型涉及发方、收方、敌方以及仲裁4个参与方以及5种攻击。敌方可对系统进行模仿攻击(I)和替换攻击(S),发方可进行模仿攻击(T),收方可进行模仿攻击(R0)和替换攻击(R1)。关于这5种攻击的定义见文献[2],它们攻击成功的概率分别记为 PI,PS,PT,PR0和 PR1。仲裁了解通信系统的全部但不参与通信活动,只有当发方与收方发生争端时才出面解决争端,因此假定仲裁是诚实的。下面给出 A2-码的定义。

JOHANSSON在文献[2]中用射影几何 PG(3,Fq)构作了2个完备的 A2-码,李瑞虎等在文献[3]中用射影几何 PG(n,Fq),n≥3构作了一类完备的 A2-码,推广了文献[2]中的构作 Ⅰ。笔者用射影几何PG(n,Fq),n≥5构作了一类新的带仲裁的认证码,计算了有关的参数,并证明了它在一定条件下是完备的。
1 射影几何的预备知识
由文献[4]可知下面的命题成立。
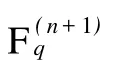
由文献[5]对于 F(n)q的向量子空间可知下面的命题成立。
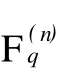
由命题2易得下面的推论。
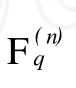
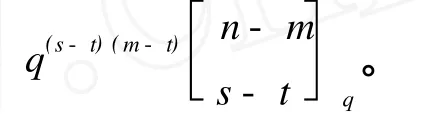
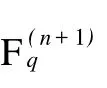
2 A2-码的构作

证 明 1)由dim(S∪ET)+dim(S∩ET)=dim S+dim ET可知,
dim(S∪ET)=dim S+dim ET-dim(S∩ET)=r+2,故S∪ET是一个信息。
2)设另有 S′,使 S′∪ET=M,则 S′⊂ (M ∩P0),由维数关系 S′=M∩P0=S,唯一性得证。
定理1 上述构作是一个A2-码。
证 明 1)f,g是满射。
首先证 f是满射。由引理1中的1)可知,f已是映射。设M是一个信息,则M∩P0=S是一个信源,由于dim M=r+2>dim S=r,在 M中存在一个2维子空间Q使得Q∩P0={0},于是 ET=Q∪U是一个4维子空间(3-面)且 ET∩P0=U,也就是说 ET是一个发方编码规则,且S∪ET=M,因此 f是满射。
再证 g是满射。g显然是一个映射。任取一个信源S,必有一个信息M使得M∩P0=S,由于dim M=r+2>dim S=r,所以必存在一个一维子空间W⊂M,但是W∩P0={0},这样W∪U=ER是一个2-面,ER∩P0=U,即 ER是一个收方编码规则,且 ER⊂M,故 g是满射。
2)由引理1中的2)可知S由M和 ET唯一确定。
3)若 P(ET,ER)≠0(即 ER⊂ ET)且 f(S,ET)=M,由 M=S∪ET,知 ER⊂ M,因此 g(M,ER)=S,否则g(M,ER)={欺诈}。
定理2 上述构作所得A2-码具有以下参数:
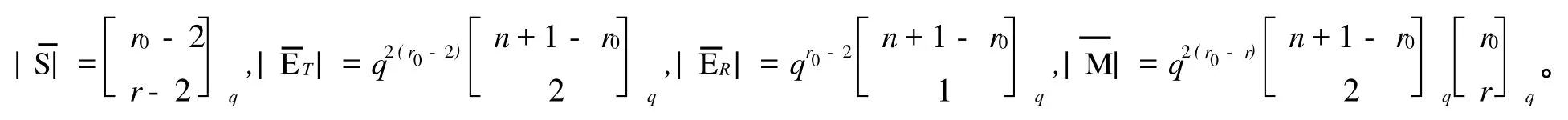
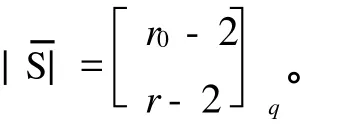
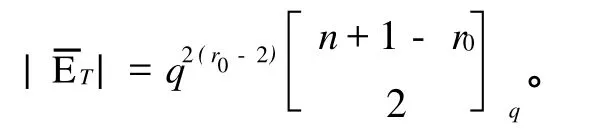
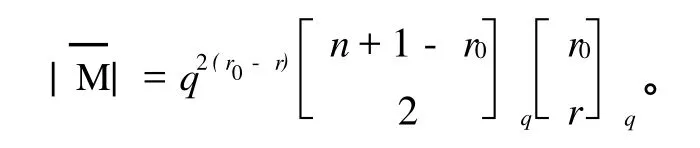
证 明 1)因为U⊂(ET∩ER),又 ET包含 ER,c相当于包含在一个给定2维空间中的1维子空间的个数,易得:
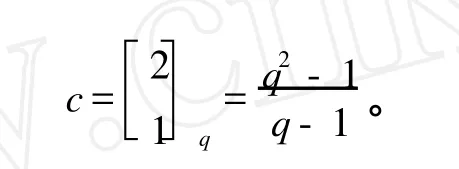
2)因为U⊂(ET∩ER),d相当于求包含一个给定3维空间 ER的满足ET∩P0=U的4维子空间的 ET的个数。由于一般线性群可迁地作用在同维子空间的集合上,这样可以设:于是,满足条件的子空间 ET的矩阵表示具有下面的形式:
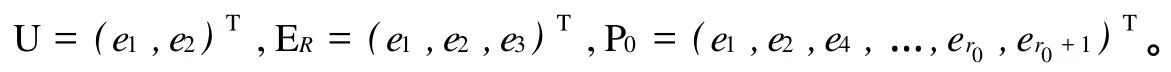
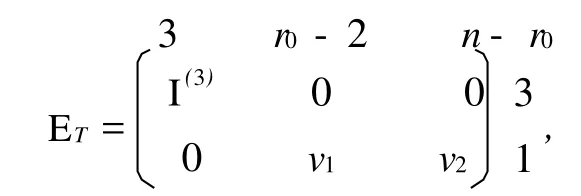
其中:v1是任意的(r0-2)维行向量;v2是不为零的(n-r0)维行向量,故经简单计算可得:
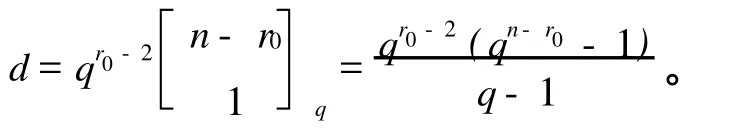
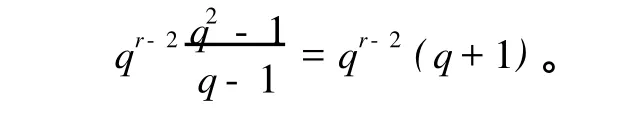
证 明 1)由题意得 ER⊂ET⊂M,不妨设U=(e1,e2)T,ER=(e1,e2,e3)T,P0=(e1,e2,e4,…,er0,er0+1)T,M=(e1,e2,e3,e4,…,er,er0+1,er0+2)T。
于是,满足条件的子空间 ET的矩阵表示具有下面的形式:
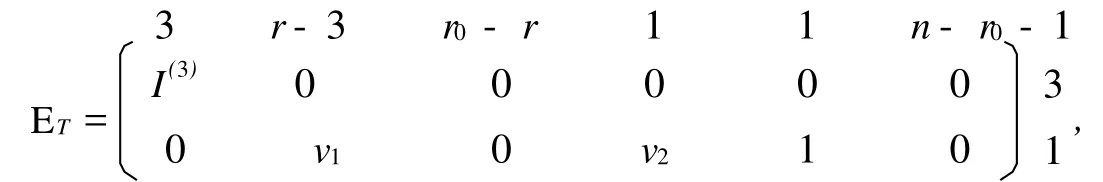
其中:v1是任意的(r-3)维行向量;v2是 Fq中的任意元素,故易得所求个数为qr-2。
2)用同1)类似的方法计算即得。
引理4 若 M1与 M2是共同包含发方的一个编码规则′的2个不同信息,S1与S2分别为 M1与 M2包含的信源,设S0=S1∩S2,dim S0=k,则2≤k≤r-1,并且有如下成立。
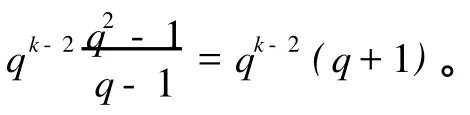
2)任取 ER⊂(M1∩M2),M1∩M2中包含 ER的 ET的个数为qk-2。
证 明 dim(M1∩M2)=dim(S1∩S2)+dim ET′-dim(S1∩S2∩ET′)=k+4-2=k+2,因为 M1∩M 2∩ER=U,dim(M1∩M2∩P0)=dim(S1∩S2)=k,用和引理3同样的方法可得。
定理3 在构作所得的A2-码中,若编码规则按等概率分布选取,则各种攻击成功的概率分别如下:
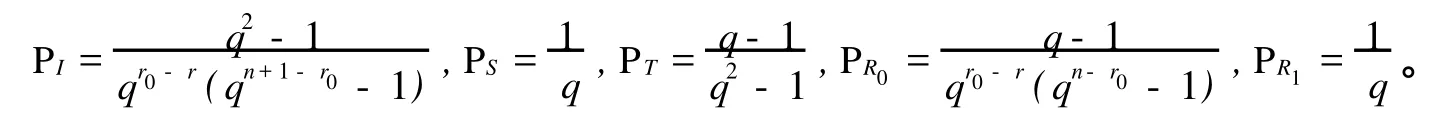
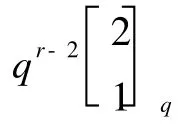
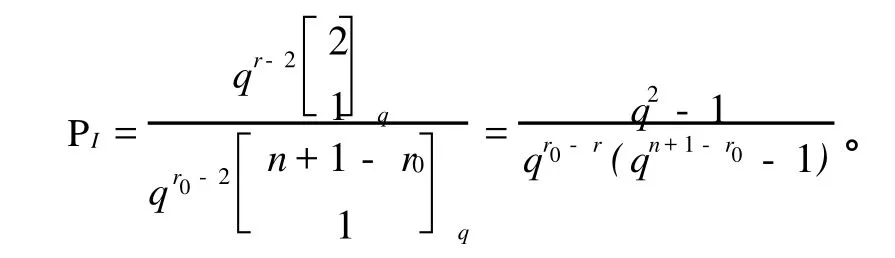
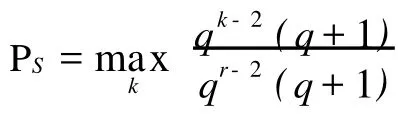
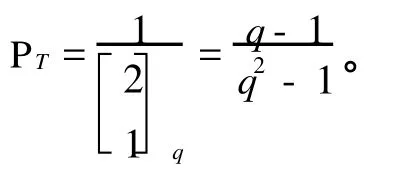
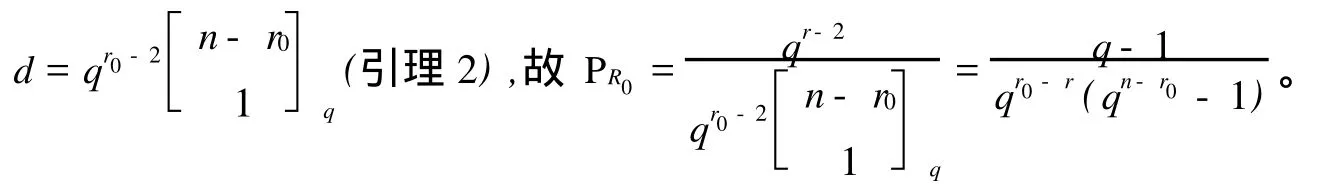
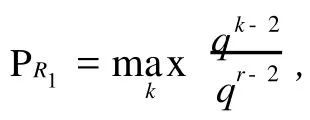
由定理2和定理3易知这个构作当 r=3时是完备的A2-码。
[1] SIMMONS G J.Message authentication w ith arbitration of transmitter/receiver disputes[A].Chaum DPriceW L.Proc Eurocrypt′87[C].Berlin:Sp ringer Verlag,1988.151-165.
[2] JOHANSSON T.Lower bounds on the p robability of decep tion in authentication w ith arbitration[J].IEEE Transactions on Info rmation Theory,1994,40(5):1 573-1 585.
[3] 李瑞虎,李尊贤.利用射影几何构作一类完备的A2-码[J].通信保密(Communications Privacy),1997,37(3):72-76.
[4] WAN Zhe-xian.Geometry of Classical Groups over Finite Fields[M].2nd Ed.Beijing/New York:Science Press,2002.61-106.
[5] 郭 军,霍元极,赵东明.有限向量空间中子空间的计数公式及其应用[J].河北师范大学学报(Journal of Hebei Normal University(Natural Science Edition)),2004,28(6):561-564.
[6] SIMMONS G J.Authentication theory/coding theory[A].Advances in Cryptology-Crypto’84,Lecture Notes in Computer Science 196[C].Berlin:Springer-Verlag,1985.411-431.
[7] 李 莉,霍丽君,李志梅.辛几何上具有仲裁的认证码的一类新构作[J].河北科技大学学报(Journal of Hebei University of Science and Technology),2010,31(4):294-299.
New construction of A2-codes based on p rojective geometry
ZHANG Xiao-han1,WANGWen-xian2
(1.Department of Basic Courses,Hengshui Vocational Technology Institute,Hengshui Hebei053000,China;2.Mathematics and Info rmation Science College,Hebei Normal University,Shijiazhuang Hebei050016,China)
In this paper,a new construction of A2-codes based on p rojective geometry is given,and the parameters are computed.Assuming that the p robability distribution of all the rules are unifo rm,the p robabilitiesof successful attacks are also computed.
authentication codes;authentication codes w ith arbitration;p rojective geometry
O157.4
A
1008-1542(2011)01-0011-04
2010-07-12;
2010-10-15;责任编辑:张 军
河北省自然科学基金资助项目(A 2008000128);河北省教育厅自然科学基金资助项目(2007127)
张晓寒(1972-),女,河北武邑人,副教授,硕士,主要从事代数与代数组合论方面的研究。

