含噪音高频数据动态整合估计波动率的方法

何成洁， 杜雪樵， 叶绪国

（1.安徽奇瑞汽车销售有限公司，芜湖 241009； 2.合肥工业大学数学学院，合肥 230009；3.凯里学院理学院，贵州凯里 556011）

含噪音高频数据动态整合估计波动率的方法

何成洁1， 杜雪樵2， 叶绪国3

（1.安徽奇瑞汽车销售有限公司，芜湖 241009； 2.合肥工业大学数学学院，合肥 230009；3.凯里学院理学院，贵州凯里 556011）

时间域和状态域方法是两种常见的非参数估计方法.前者主要使用的是最近的历史数据，而后者则主要依赖于过去的历史信息.本文在时间域上，通过对含噪音高频数据采用双时间尺度方法获得其波动率，进而获得经动态整合后的波动率.

动态整合；时间域；状态域；双时间尺度；波动率

1 引 言

高频数据指日与日内的数据，主要以小时、分钟或秒为采集频率的、按时间先后顺序排列的数据.高频数据分析是对波动率的估计和预测.在金融市场上，信息是连续性的影响证券价格过程，离散数据必然会造成信息的丢失，数据频率越低，则信息丢失越多，所以高频数据包含更多的信息.对高频数据的分析，Andersen和Bollerslev等人提出了已实现波动率［1－3］度量资产价格波动的方法.Christensen针对已实现波动率的缺陷提出了已实现极差［4］的方法.文献［5］利用双时间尺度的方法得到波动率的估计，Fan通过时间和状态域［6］上的整合对波动率给予了估计.国内王春峰、唐勇［7，8］等分别从不同角度对高频数据做了理论及实证上的研究.本文在考虑噪音的情况下，运用双时间尺度的方法，引入动态权对波动率进行整合估计，得出了含噪音高频数据的动态整合估计.

2 模型的建立

在金融市场中，如果我们要预测未来的事情或做出一个投资计划，那么要考虑两种有用的信息：时间域上的信息和状态域上的信息.Fan Jian－qing引入了动态权ωt（0≤ωt≤1）对两个渐进独立的估计进行了动态整合（参看［6］Theorem），并定义产生的整合估计为

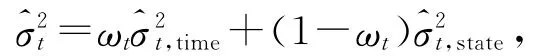
这里分别表示时间域、状态域波动率估计量.整合估计的方差最小化，这样估计效果最佳，从而得到最佳的动态权为

本文在文献［6］的基础上，在时间域上增加了噪音因素，得到了在含噪音高频数据下的动态整合估计波动率的方法.

我们考虑收益过程r，服从伊腾微分方程：

W t是一个Wiener过程.假设现在时刻为t，我们有从（2）中获得的T时间段内取样间隔是Δ的历史数据，目的是估计波动率≡σ2（rt）.

设Y i＝Δ－1／2（－）＝＋，其中为在t i时刻的观测值，是历史数据是真实值.是i.i.d微观结构噪音，满足

且与独立.

1.状态域.

对于状态域，由文献［6］，设

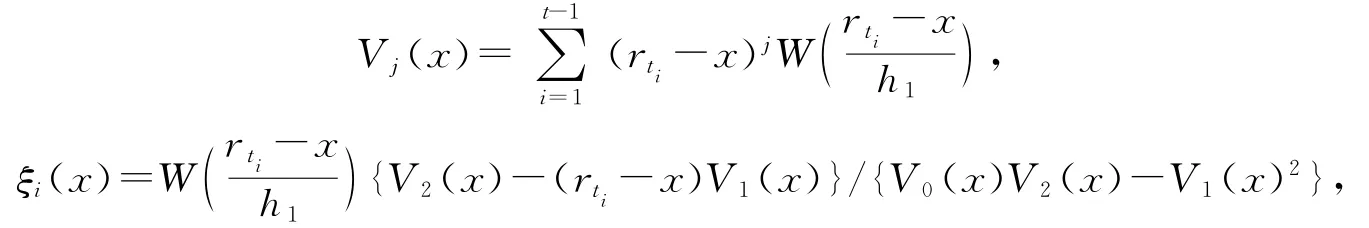
w（·）表示核函数，则局部线性估计可表示为

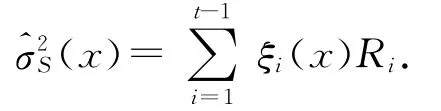
这里Ri＝｛Y i－f（）｝2表示条件项平方（squared residuals）.其渐近方差为

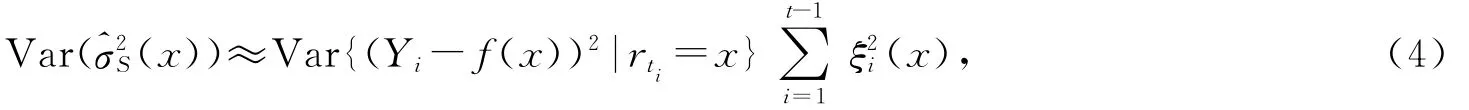
这里我们不妨设εi～N（0，1）时，

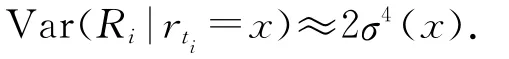
2.时间域.

对波动率采用移动平均模型MA来估计

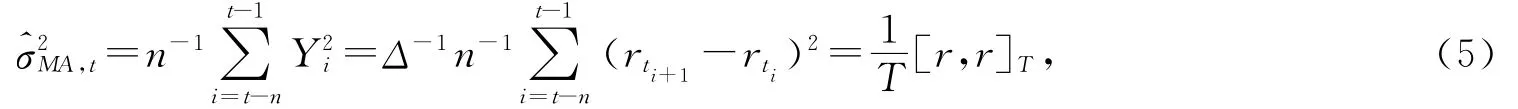
其中［r，r］T表示在［0，T］时段上r的二次变差.

我们分两种情况来看：一种是噪音存在但被忽略了，另一种情况是考虑了噪音因素.

（i）噪音存在但被忽略.

假定市场微观结构噪音存在，但在估计波动率时，噪音被忽略了，即我们用观值作为来估计波动率，由模型（5）有

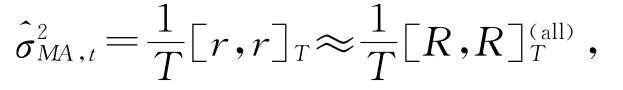
其中［R，R表示在［0，T］时段上，R取得所有观测值时的二次变差.

事实上，在＝＋下，观测值有如下的二次变差

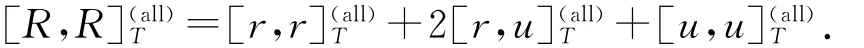
给定（3），我们可知［R，R在r下的条件期望为

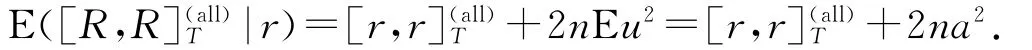
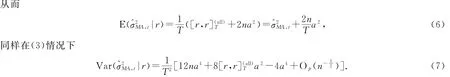
（7）的证明参见文献［5］.

（ii）考虑噪音因素.

当市场微观结构噪音存在时，表示如果考虑了噪音因素，则对于收益模型Rti＝rti＋uti，我们采用双时间尺度的方法来获得［r，r］T的估计.

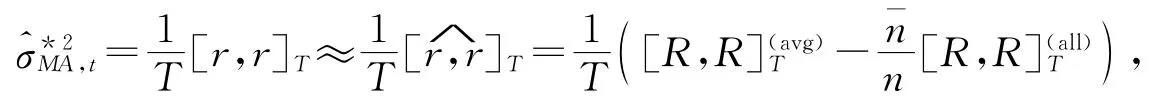
其中［r，r］T表示［r，r］T的估计量，［R，R表示在［0，T］时段上，R对所有观测值子格取样平均下的二次变差.

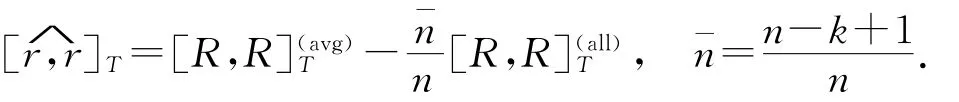
k表示子格数.（相关概念和定义参见附录）.

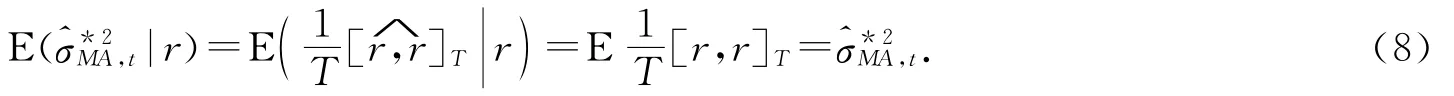
（8）的证明见附录.

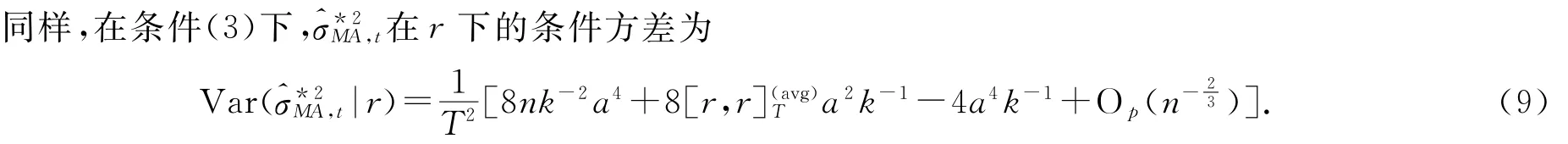
（9）的证明参见文献［5］.

3.整合估计.

在上面两种情况下，我们分别得到相应的动态权及整合估计.

由（1），（4），（7），全部数据的经典的滑动平均整合估计的动态权为

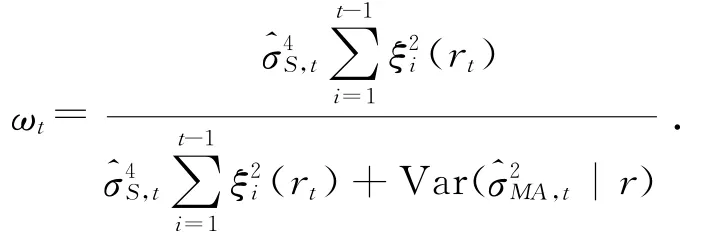
从而得到整合估计

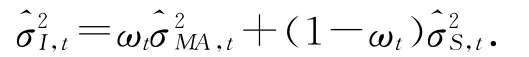
由（1），（4），（9），双时间尺度的滑动平均整合估计的动态权为

3 模拟及结论

1.定理：当n无限大时，双时间尺度的滑动平均估计的均方误差总是比全部数据所获得的经典的滑动平均估计的均方误差小.（证明见附录）

2.通过模拟，我们会发现，在存在微观市场结构噪音情况下，双时间尺度整合估计较经典的滑动平均整合估计优越.

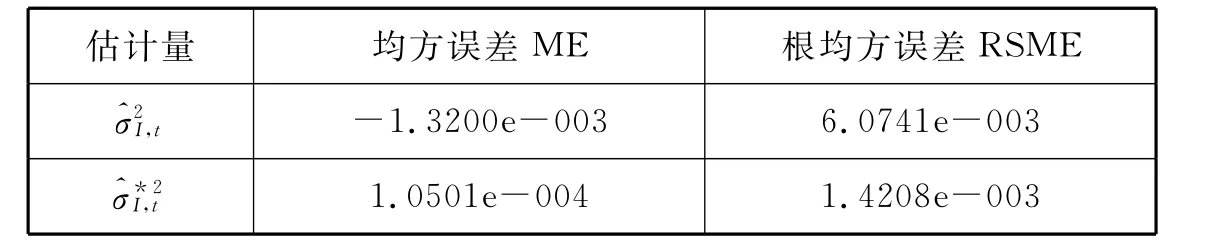
估计量 均方误差ME 根均方误差RSME＾σ2I，t －1.3200e－003 6.0741e－003＾σ＊2I，t 1.0501e－004 1.4208e－003

说明：对2004年美国短期国库券收益取样，样本量为1000，重复取样1158次，对估计量的均方误差及根均方误差进行模拟比较.在这种模拟下，我们看到的均方误差及根均方误差比的小，因此可以认为效果好.

附录

定义1 全格：全格是包含所有观测点的集合，即G＝｛t0，…，tn｝.

定义2 子格：对于一个任意格H，H⊆G.如果ti∈H，ti，－，ti，＋分别表示H中位于t i之前和之后的元素，而ti仍然是全格G中第i个元素，则称H为G的子格.

定义3 二次变差：对在任意子格H⊆G上的随机过程X，我们定义二次变差［X，X］如下

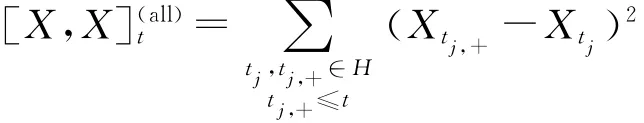
在全格G上X的二次变差可以写成

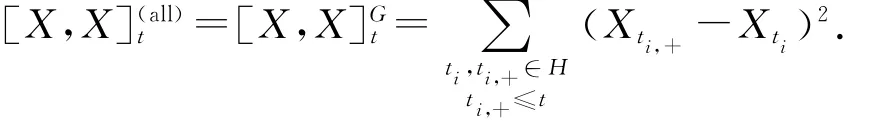
通常情况下，若特别强调在某个格上，X的二次变差

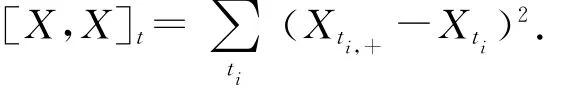
定义4 二次协变差：类似二次变差的定义，我们定义二次协变差，设Z＝X＋Y，X，Y，Z表示随机过程，［Z，Z］t＝［X，X］t＋2［X，Y］t＋［Y，Y］t.

引理假设r是形如（2）的Itô过程，若R与r的关系如（3），且对∀i，ti，ti＋1不在同一个子格中，则在条件r下有

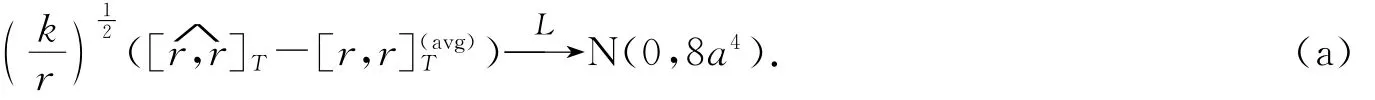
证明见文献［2］.

引理（过滤的描述） 对任意p，x＝（x（1），x（2），…，x（p））是多维连续的P局部鞅，因此Ft是包含σ（x s，s≤T）和N的最小σ－代数，其中N是σ（x s，s≤T）中的所有空集，有

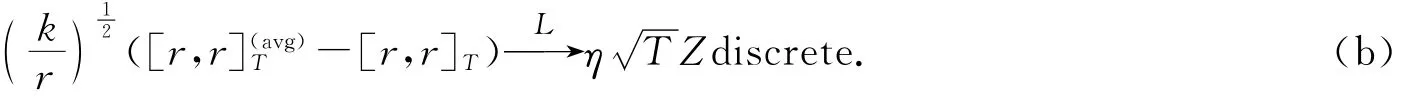
其中η是某个常数，Zdiscrete是与r独立的标准正态分布.

证明见文献［2］.

（8）的证明

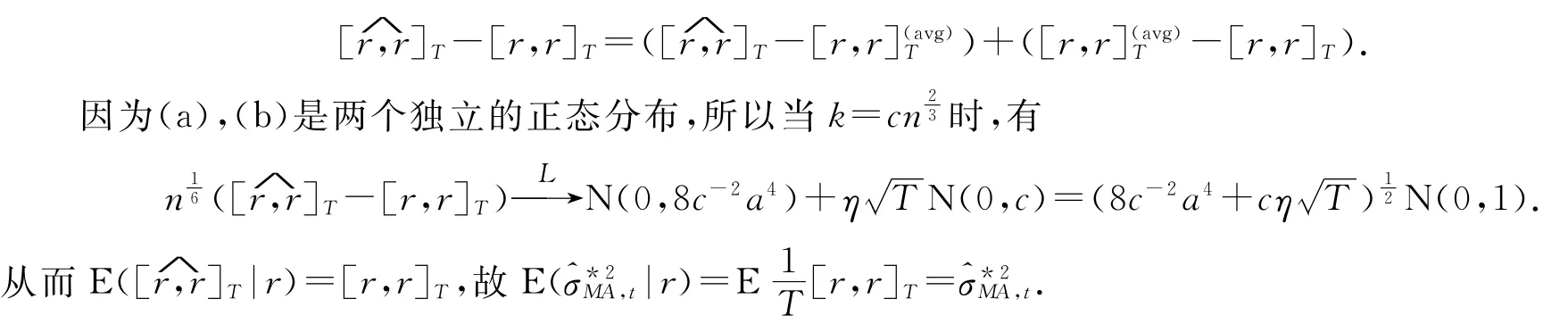
定理当n无限大时，双时间尺度的滑动平均估计的均方误差总是比全部数据所获得的经典滑动平均估计的均方误差小.

证由（6），（7），全部数据所获得的经典的滑动平均估计的均方误差为

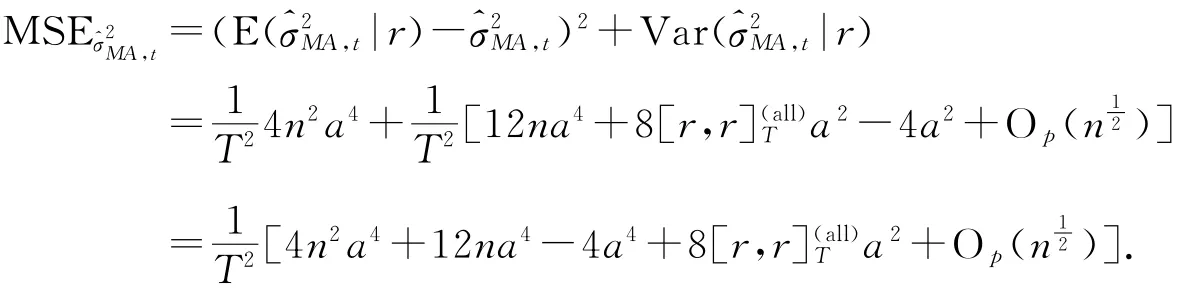
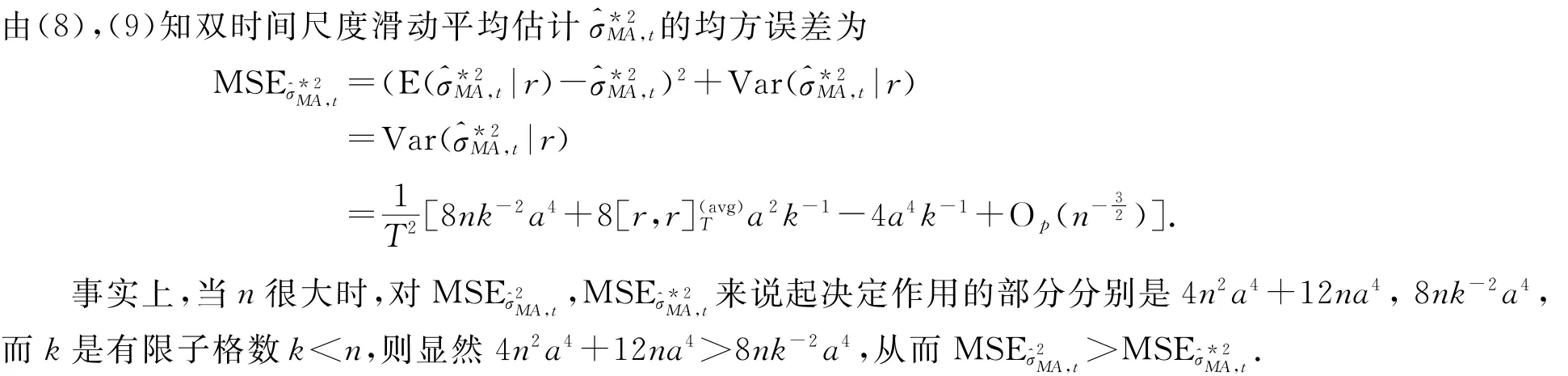
［1］Andersen T G.Bollerslev T et al.Exchange rate returns standardized by realized volatility are（nearly）Gaussian［J］.Multinational Finance Journal，2000，4：159－179.

［2］Andersen T G.Bollerslev T et al.The distribution of realized exchange rate volatility［J］.Journal of American Statistical Association，2001，96（453）：42－55.

［3］Andersen T G.Bollerslev T et al.The distribution of realized stock return volatility［J］.Journal of Financial Economics，2001，61（1）：43－76.

［4］Christensen K，Podolskij M.Asymptotic theory for range－based estimation of integrated variance of a continuous semi－martingale［R］.A arhus School of Business，2005.

［5］Zhang L，P A Mykland，Y Ait－Sahalia.A tale of two time scales：determining integrated volatility with noisy high－frequency data［J］.Journal of the American Statistical Association，2005，100（472）：1394－1411.

［6］Fan J，Fan Y，Jiang J.Dynamic integration of time－and state－domain methods for volatility estimation［J／L］.http：∥arxiv.org／abs／math.St／0506029，2005－06－02.

［7］王春峰，等.高频数据下投资组合风险预测模型比较［J］.系统工程，2007，25（3）：23－28.

［8］唐勇，张世英.高频数据的加权已实现极差波动及其实证分析［J］.系统工程，2006，24（8）：52－57.

Dynamic Integration Methods for Volatility Estimation with Noisy High－Frequency Data

HECheng－jie1，DUXue－qiao2，YEXu－guo3

（1.Anhui Chery Automobile Sales Co.，Ltd.，Wuhu 241009，China；2.Department of Mathematics，Hefei University of Technology，Hefei 230009，China；3.School of Science and Physics，Kaili University，Kaili，Guizhou 556011，China）

Time－and state－domain methods are two common approaches for nonparametric prediction.The former predominantly uses the data in the recent history while the latter mainly relies on historical information.The paper adds the affect of noisy in time－domain，and obtains the volatility of noisy high frequency data by two time scales method，then get the dynamic integration volatility.

dynamic integration；time－domain；state－domain；two time scales；volatility

O212.2

A

1672－1454（2011）04－0108－05

2008－09－ ；［修改日期］2009－06－19