双连续N次积分C－半群的逼近定理

秦喜梅， 钱 云

（巢湖学院数学系，安徽巢湖 238000）

双连续N次积分C－半群的逼近定理

秦喜梅， 钱 云

（巢湖学院数学系，安徽巢湖 238000）

在C0半群和双连续半群逼近定理的启发下，讨论了双连续n次积分C－半群的逼近定理.

双连续；n次积分C－半群；双等度连续；生成元

1 引 言

近年来对有界连续（或一致连续）函数空间上半群的研究，引起了人们对Banach空间上非强连续半群的研究.Kǔhnemund在Banach空间上另外附加一个比范数拓扑粗的局部凸拓扑，使得半群在这个局部凸拓扑下强连续，由此提出了双连续半群的概念，为半群理论的研究开辟了新的研究领域，说明了双连续半群理论有很好的前景和研究价值.

本文讨论的双连续n次积分C－半群所在的空间要满足：

设（X，‖·‖）是Banach空间，其共轭空间是X′，τ是X上的一个局部凸拓扑并具有如下性质：

（i）空间（X，τ）在‖·‖－有界集上序列完备，即每个‖·‖－有界的τ－柯西列在（X，τ）中收敛；

（ii）拓扑τ比‖·‖－拓扑粗且τ是Hausdorff拓扑；

（iii）空间（X，‖·‖）中的范数可由空间（X，τ）′定义，即对每个x∈X，有

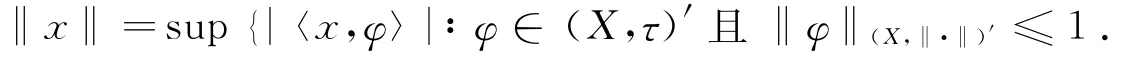
为了方便，记Φ＝｛φ∈（X，τ）′∶‖φ‖（X，‖·‖）′≤1｝.Pτ表示X上的局部凸τ拓扑τ所对应的半范数族.由约定，不失一般性，假定p（x）≤‖x‖，∀x∈X，p∈Pτ.

如不特别说明，本文中的积分均是在τ－拓扑意义下的积分，算子C∈B（X）为单射.

2 双连续n次积分C－半群的概念和性质

下面给出双连续n次积分C－半群的定义.以下记（M，ω，C）表示空间X上的指数有界的双连续n次分C－半群全体.

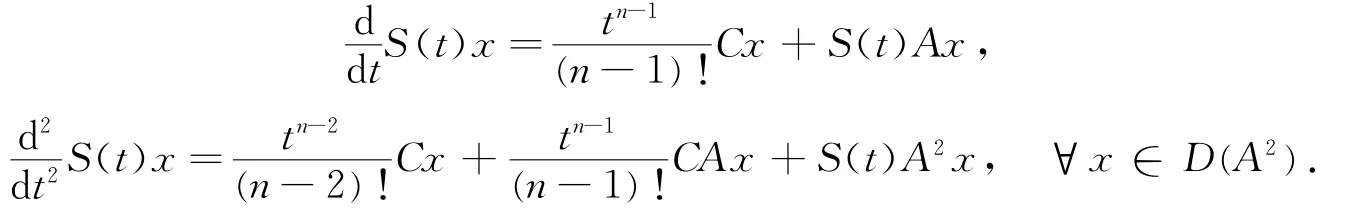
一般情形可以由归纳法证明.

（ii）由（i）易证.

（iii）由（i）知对任意x∈D（An＋1），有

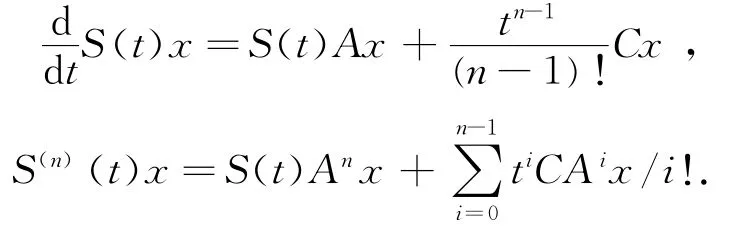
对上式两端关于t再求一次导数，得

3 双连续n次积分C－半群的逼近定理

［1］Albanese A，Mangino E.Trotter－Kato theorems for bi－continuous semigroups and applications to Feller semigroups［J］.J.Math.Anal.Appl.，2004，289（2）：477－492.

［2］Kǔhnemund F.A Hille－Yosida theorem for bi－continuous semigroups［J］.Semigroup Forum，2003，67（2）：205－225.

［3］Xiao Tijun，Liang Jin.Approximation of Lapace transforms and integrated semigroups［J］.Joural of Function Analysis，2000，172（1）：202－220.

［4］Liang Jin，Xiao Tijun.Higher order abstract Cauchy problem：their existence and uniqueness families［J］.J.London Math.Soc.，2003，67（1）：149－164.

［5］Liang Jin，Xiao Tijun，Li Fang.Multiplicative perturbations of localC－regularized semigroups［J］.Semigroup Forum，2006，72（3）：375－386.

［6］Sun Guozheng.Representation theorem for mildC－existence families［J］.Northeast Math.，1999，15（4）：469－472.

［7］Delaubenfels R.，Sun Guozheng，Wang Shengwang.Regularized semigroups，existence families and the abstract Cauchy problem［J］.Differential Integral Equations，1995，8（6）：1477－1496.

［8］Lizama C.On the convergence and approximation of integrated semigroups［J］.Math.Anal.Appl.，1994，181（1）：89－103.

［9］Zheng Quan.Perturbation and approximations of integratedC－semigroups［J］.Acta.Math.Sinica，New Series，1993，9（3）：252－260.

［10］秦喜梅，葛国菊.指数有界的双连续n次积分C－半群及其生成逼近定理［J］.大学数学，2008，24（3）：104－111.

The Approximation Theorem for Bi－ContinuousN－times IntegratedC－Semigroups

QINXi－mei，QIANYun
（Department of Mathematics，Chaohu College，Chaohu Anhui 238000，China）

Inspired by the approximation theorems forC0semigroups and bi－continuous semigroups，we discuss the approximation theorems for bi－continuousntimes integratedC－semigroups.

bi－continuous；Ntimes integratedC－semigroup；bi－equicontinuous；generator

O177

A

1672－1454（2011）04－0103－05

2008－09－09

安徽省教育厅自然科学研究项目（KJ2010B127；KJ2009B097）