带有误差为正态分布的SUR回归的贝叶斯分析及其应用
曾婉红,刘金山
(华南农业大学理学院,广州510642)
带有误差为正态分布的SUR回归的贝叶斯分析及其应用
曾婉红,刘金山
(华南农业大学理学院,广州510642)
文章研究了带有正态分布SUR模型,采用Jeffreys的不变先验分析Gibbs抽样方法和Direct Monte Carlo(DMC)方法,计算了各参数的贝叶斯后验密度和未来值的预测密度以及其它相关的后验量,如后验置信区间等。通过模拟例子和建立了关于城镇、农村居民家庭平均收入和生活消费支出的SUR模型,将Gibbs抽样方法和DMC方法得出的结果进行了比较。
正态分布SUR模型;Jeffreys的不变先验;Gibbs抽样方法;Direct Monte Carlo;贝叶斯后验密度;预测密度
0 引言
Arnold Zellner的经典文章“An Efficient Methods for Estimating Seemingly Unrelated Regressions and Tests of Aggregation of Bias”引进了SUR模型,该文章具有里程碑意义,它极大地刺激了在计量经济学和其它领域的深入的理论研究和无数的应用研究。
由于SUR模型在计量经济学中的重要性,本文拟通过一个模拟例子和建立关于城镇和农村居民家庭平均收入和生活消费支出的SUR模型。在误差序列服从多元正态分布的假设前提下,分析SUR模型的贝叶斯方法之一的是MCMC方法。目前,在贝叶斯分析中应用最为广泛的MCMC方法主要有两种:Gibbs抽样方法和Metroplis-Hastings方法。本文采用Gibbs抽样方法。使用Gibbs可以近似每个参数的后验密度和对未来值构造贝叶斯预测密度。近年来,计算机技术的发展使得MCMC技术被广泛得使用。
然而Gibbs抽样方法的使用会出现一些问题:首先,预迭代的个数不确定;第二,没有统一的规则决定Gibbs的样本量;第三,必须检验Gibbs方法的收敛性。虽然提出了很多检验Gibbs方法收敛性的方法,但都不能保证在有限的运行中Gibbs方法能从所需要的后验分布中产生样本。
最近,Zellner和Anod(2008)提出了一种新的有效的贝叶斯估计方法,它是基于直接蒙特卡罗(DMC)方法,采用Jeffreys’s的不变先验,构造“递归”的联合后验密度,这种方法不会出现Gibbs方法以上的问题。
1 SUR的Gibbs方法和DMC方法
1.1 标准SUR模型
考虑由m个回归方程组成的系统:
这里,yj和uj都是n×1维向量,Xj是n×pj维观察值矩阵,βj是pj维系数向量,Ω是m×m矩阵,对角元素为非对角元素为ωij。参数值域如下:

方程(1)中表明每个方程有不同的独立变量和方差,而且允许不同方程中的误差项在同一观察时间上是相关的。将(1)写成矩阵形式:

(1)β的满条件分布

(2)Ω的满条件分布
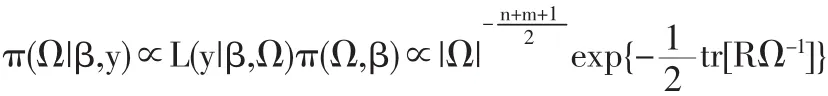
Gibbs抽样算法如下。
首先赋初始值Ω(0),Ω(0),第j次迭代:
①从满条件分布π(β|Ω(j-1),y)中抽取β(j);
②从满条件分布π(Ω|β(j),y)中抽取Ω(j)。
1.2 用于SUR模型的直接蒙特卡罗方法
最近,Zellner和Ando(2008)得到一种直接蒙特卡罗过程,用于SUR模型的贝叶斯分析。我们将方程(1)重新表述为如下形式:

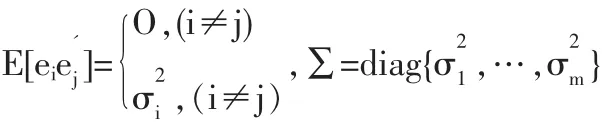
Zj是βj-1,…,β1的函数,参数的似然函数为:


其中|J|是由{β,Ω}到{b,Σ}的雅克比行列式。参数θ的联合后验密度为:
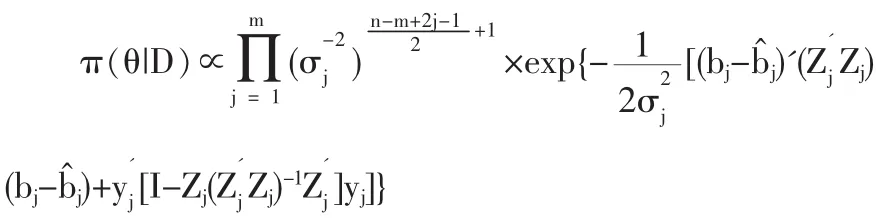
①bj的条件后验密度:


直接蒙特卡罗过程如下:
步骤1(初始化)固定m。设定产产生的样本数N,令j=1。产生,插入样本值到然后从中生成一个样本
步骤3有顺序地重复步骤2直到j=m。
步骤4将Σ(k)转换成Ω(k)。
步骤5从多元正态分布中抽取β(k),均值为,协方差为矩阵
2 模型预测
采用选择的模型和对应的后验样本{β(k),Ω(k);k=1,…,N},可评估各种量。例如,预测密度可近似为:

这样不仅可以得到参数的后验密度,还可计算参数的各种函数的后验密度,例如,多项式、率、根及其他表示参数的特征的量。
3 算例
为了评估本文提出的抽样过程,在此展现基于模拟数据和真实数据建立模型并进行分析。本文所有的程序的实现都是使用R软件。
3.1 随机模拟
为了研究本文贝叶斯模型估计过程的特征,模拟m=3维的SUR模型(1),不失一般性,设定pj=2;j=1,2,3;i=1,2,…,n;n=100,Ω={ωij}。


表1 DMC和Gibbs方法的统计结果
两种方法均抽取N=10000个样本进行统计计算。
(1)采用Gibbs抽样方法时进行迭代11000次,然后丢弃前面的1000次迭代,即剩下10000个样本,而采用DMC方法直接抽取10000个样本,结果见表1、图1。

由表1得,采用Gibbs方法和DMC方法得出的参数估计值相近,而且均接近模拟时所
设置的参数值,各估计值均在95%置信区间内;收敛性诊断是采用Heidelberger和Welch的收敛性诊断结果,结果表明各参数在所抽取的马尔可夫链均收敛。
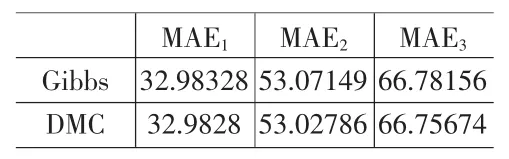
表2 平均绝对误差值

由表3、4得,上述两种方法得出的预测估计值均能很好地接近真实值,且得出的预测估计值相差不大。图3为一步估计预测密度图。

表3 y1,y2,y3的预测密度统计,预测估计点x1=-2,x2=-3,x3=2

表4 DMC与Gibbs方法的预测值比较,预测估计点x1=-2,x2=-3,x3=2

(2)重复实验
重复该模拟实验100次,在DMC抽样中每次抽取样本量为10000,而Gibbs抽样中每次抽取11000个样本,然后丢弃前面的1000次迭代,剩下10000个样本,将每次实验得到的均值再求平均,结果见表5。从结果看出,各参数的后验均值(即估计值)更加接近于真实值,说明重复多次实验会使结果更加的精确。

表5 重复100次试验后DMC与Gibbs方法的统计结果
2.2 应用实例
2.2.1 数据来源
研究1980~2008年中国城镇居民家庭人均可支配收入与生活消费支出以及农村居民家庭人均纯收入与生活消费支出(数据来源于《新中国六十年统计资料汇编》)的关系。本文采用1980~2007年的数据建立模型,共28组数据,而2008年数据用于预测。
2.2.2 建立模型
建立以下的SUR模型:
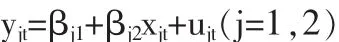
其中表示1980~2008年,y1t,y2t分别代表城镇、农村居民家庭人均生活消费支出,x1t代表城镇居民家庭人均可支配收入,x2t代表农村居民家庭人均纯收入。假设两个回归方程的误差在同一时刻是相关的,即(u1t,u2t)~N(0,Ω)。现分别采用Gibbs和DMC方法分析该模型,得到的结果见表6~9,图4~5。
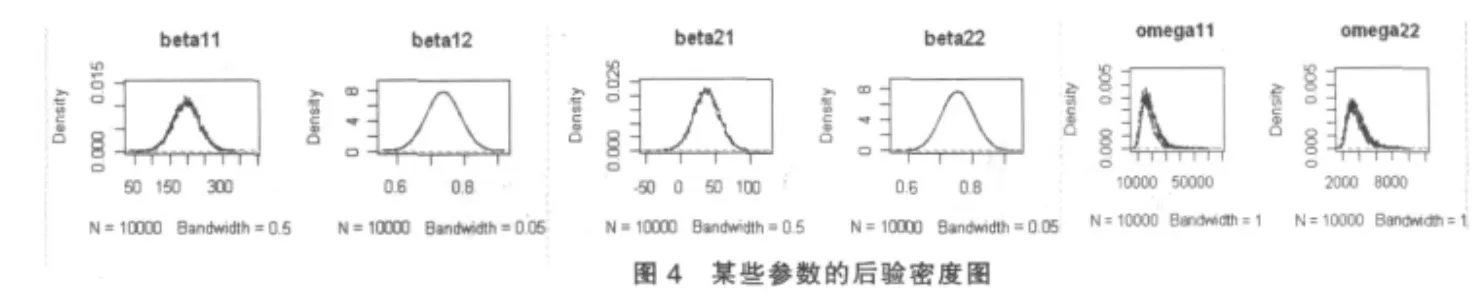
由表6得:采用Gibbs方法比DMC方法得出的参数估计值相近,各估计值均在95%置信区间内;根据Heidelberger和Welch的收敛性诊断,各参数抽取的马尔可夫链均收敛;城镇居民家庭人均可支配收入与农村居民家庭人均纯收入对生活消费支出的贡献均大于0,说明人均收入能推动人均消费。从表7看出,采用这两种方法得到的平均绝对误差非常接近。图4为某些参数的后验密度图。

表6 DMC和Gibbs方法的统计结果
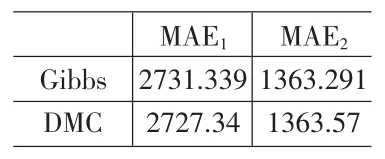
表7 平均绝对误差值
由表8和9得,上述两种方法得出的预测估计值均能很好地接近真实值,且得出的预测估计值相差不大。图5为2008年城镇、农村居民家庭人均生活消费支出估计的预测密度图。

表8 y1,y2的预测密度统计,预测估计点x1=15780,x2=4760.6

表9 DMC与Gibbs方法的预测值比较

4 结论
本文主要使用了两种贝叶斯方法分析带有误差为正态分布的SUR模型,一种是直接蒙特卡罗方法(DMC),另一种是Gibbs抽样方法。这两种方法得到的结果基本上是一致的,而且得出的参数估计值均能很好地近似于真实值。但是DMC方法比Gibbs抽样方法使用起来更加的简便。它们的区别见表10。

表10 DMC与Gibbs的比较
在应用实例中可得,城镇(农村)居民人均生活消费支出是随着城镇居民家庭人均可支配收入(农村居民家庭人均纯收入)的提高而增加的,这与实际情况相符合。
[1]S.Chib,E.Greenberg.Hierarchical Analysis of SUR Models with Extensions to Correlated Series and Time-Varying Parameter Models[J].Econometrics,1995,68.
[2]George Casella,Edward I.George.Explaining the Gibbs Sampler[J].The American Statistician,1992,46(3).
[3]Tomohiro Ando,Arnold Zellner.Hierarchical Bayesian Analysis of the Seemingly Unrelated Regression and Simultaneous Equations Models Using a Combination of Direct Monte Carlo and Importance Sampling Techniques[J].Bayesian Analysis,2010,5(1).
[4]Arnold Zellner,Tomohiro Ando.A Direct Monte Carlo Approach for Bayesian Analysis of the Seemingly Unrelated Regression Model[J].Journal of Econmetrics,2010,159(1).
[5]Arnold Zellner,Tomohiro Ando.Bayesian and Non-Bayesian Analysis of the Seemingly Unrelated Regression Model with Student-t errors,and Its Application for Forecasting[J].International Journal of Forecasting,2010,26.
[6]Chan K.S.,Geyer C.J.Discussion of Markov Chains for Exploring Posterior Distributions[J].Annals of Statistics,1995,22.
[7]Percy,D.F.Prediction for Seemingly Unrelated Regressions[J].Journal of the Royal.Statistical Society,1992,(54).
[8]Mary Kathryn Cowles,Bradley P.Carlin.Markov Chain Monte Carlo Convergence Diagnostics:A Comparative Review[J].1996,91(434).
[9]Cui,Tanner.Comment:Monitoring Convergence of the Gibbs Sampler:Further Experience with the Gibbs Stopper[J].Statistical Science,1992,(7).
O212.8
A
1002-6487(2011)07-0038-04
国家自然科学基金资助项目(10871072)
曾婉红(1985-),女,广州花都人,硕士研究生,研究方向:计算机应用技术。刘金山(1958-),男,河南方城人,教授,研究方向:贝叶斯统计。
(责任编辑/亦民)

