椭圆宏程序的逐级深入

河南 卫彩绒 裴成君

椭圆宏程序的逐级深入

河南 卫彩绒 裴成君

本文从椭圆的标准方程入手，将椭圆的宏程序分成若干细小台阶，逐级深入，介绍椭圆方程在数控车编程里的应用，椭圆车削里用到的常用循环语句（WHILE语句），以及在数控车样件中当椭圆处于不同位置时编程坐标的变化，即椭圆偏移后。椭圆宏程序中坐标点的计算方法。由浅入深地讲述了椭圆这个基本的二次曲线在数控车中的车削编程应用。

卧椭圆；标准方程；WHILE循环；偏移

宏程序在数控专业学生的学习中，一向作为较深层次的指令来接受。因此感觉很是艰涩、难懂。有些学生甚至因此而放弃对这部分内容的掌握，或者降低要求、一知半解。特别是对于中等职业学校的学生来说，二次曲线部分在他们的数学课上不曾接触过，所以更是增加了学习的难度。

实际上，每个知识点，只要能够根据学生的认知规律，巧妙地设置学习的台阶，由浅入深，逐步深入，而不是大堆重点难点的堆砌，加上生动的事例，在教学中是可以收到相当理想的教学效果的。

下面，以椭圆宏程序在FANUC系统中的逐步推进的教学为例来与大家分享一下。

一、椭圆知识的简单介绍

如果把椭圆的标准方程，参数方程，极坐标方程等等全部罗列出来给学生认识，就是一大堆难以理解的式子和字母，要让学生们去生生地记忆，这对于对宏程序本就有畏惧心理的初学者来说，不啻于一个打击。所以，初起，只讲解最简单最基本的卧椭圆（长轴在水平坐标轴上）的标准方程[1]：

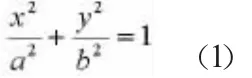
其中，（如图1所示）

图1 标准卧椭圆

a是椭圆的长半轴。

b是椭圆的短半轴。

F1，F2是椭圆的两个焦点。焦半径为c。它们之间的关系式：

天体运行的轨迹就是椭圆，若太阳在焦点F1处，则：A和B就分别是地球每年的近日点和远日点。近日点距离(AF1)为147,100,000 km，远日点距离(BF1)为152,100,000 km；同样地，若地球在焦点F1处，则：A和B就分别是月球每月的近地点和远地点。今年的近地点距离(AF1)约为：357,159km，远地点距离(BF1)约为：406,445km。

二、椭圆知识在卧式数控车编程中的应用

在卧式数控车的工件图上，均为零件的俯视图，坐标轴与数学上常用的坐标轴有些区别，如图2所示[2]。则，椭圆方程在这个坐标系上表达为：

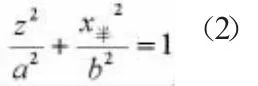
其中，

z为z方向上的坐标变量。

x半为x方向上的坐标变量。

图2 卧式数控车上的卧椭圆

一个如图3所示的椭圆，就可以用如下的公式来表达：

则，根据公式，可以用z坐标表达出坐标值：即

在数控车编程中记作[3]，

（）记作：[]；

z2，a2…记作：z*z，a*a；

公式（4）记作：

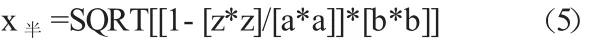
例式（3）表示为：

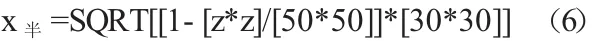
图3 卧椭圆宏程序

三、WHILE循环语句在数控车中的应用

椭圆的精车过程，实际上就是若干段微小直线的拟合过程[4]，需要用到循环语句。循环语句有WHILE循环语句、GOTO语句、IF语句等等，WHILE循环是最常用的循环语句之一，格式如下：

在数控车中，为与指令地址X，Z相区分，指令值中的变量z和x半只能用#1或#2等等的变量名来表达。

逻辑判断符号表达为：

实际中，就是用#1替代z，#2替代x半得到的。

四、零件中的卧椭圆宏程序

（一）仅Z轴偏移

为方便编程和对刀，零件中坐标系的零点通常选在工件端面O上，椭圆中心O1的坐标就有了个Z向的偏移量z0，如图4所示。

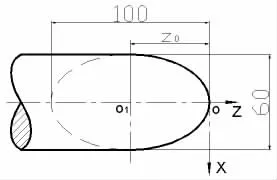
图4 Z向偏移后的卧椭圆

这时，只需要将上面程序中的Z坐标中加上一个偏移量z0即可。即

（二）X轴、Z轴都偏移

当椭圆部分在零件端面以外的其他位置时，也就是说，椭圆中心O1的坐标在Z向有一个偏移量z0，X向也有一个偏移量x0，如图5所示。

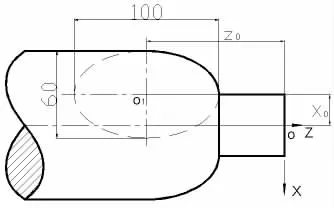
图5 X向Z向均偏移的卧椭圆

这时，只需要将上面程序中的Z坐标中加上一个偏移量z0，X坐标中加上一个偏移量x0即可。

即：

这里介绍了半个卧椭圆的宏程序的认识过程。通过这样的逐级深入，使学生们在不知觉间，逐步地进入了椭圆宏程序的编写过程，若能将每项内容与标题倒置处理，效果会更好。

[1]丘维生.数学[M].高等教育出版社，2009.

[2]沈建峰，虞俊.数控车工（高级）[M].机械工业出版社，2008.

[3]河南省职业技术教育教学研究室，数控车削技术[R].电子工业出版社，2009.

[4]楼章华，杨静云.数控编程与加工[M].中国传媒大学出版社，2008.

(作者单位：河南省三门峡中等专业学校)

（编辑 王旸）