考虑静态电压稳定性的多目标无功优化①
杨晓萍, 张 强, 薛 斌, 王 磊
(1.西安理工大学水利水电学院, 西安 710048; 2.佛山电力设计院有限公司, 佛山 528200; 3.西北电力设计院, 西安 710075)
考虑静态电压稳定性的多目标无功优化①
杨晓萍1, 张 强2, 薛 斌1, 王 磊3
(1.西安理工大学水利水电学院, 西安 710048; 2.佛山电力设计院有限公司, 佛山 528200; 3.西北电力设计院, 西安 710075)
针对遗传算法容易出现早熟、局部寻优能力较差和收敛速度缓慢的问题,该文用模拟退火思想对适应度函数进行改善,用自适应算法对遗传算法的交叉、变异策略进行改进,采用精英保留策略,变异操作作用尾部占优原则,并把基于广义Tellegen定理的电压稳定裕度指标最小作为无功优化的目标函数之一,以改善电力系统的静态电压稳定性。用IEEE14、IEEE30和IEEE57节点系统进行验算,将优化结果与其他算法进行比较,表明本文算法优化结果更优,相对于简单遗传算法有更好地收敛性,加速了算法的收敛速度,在降低网损的同时能够有效提高负荷节点的电压稳定裕度。
电力系统; 无功优化; 静态电压稳定; 裕度指标; 改进遗传算法
电力系统无功优化是以满足系统负荷要求和各种运行约束为前提,通过优化计算确定发电机的端电压、有载变压器的分接头档位和无功补偿设备的容量等,达到有功网损最小、电压质量最优等目标的综合优化问题。传统的优化算法如线性规划法[1]、非线性规划法[2]、灵敏度法[3]等容易陷入局部最优解,因此,许多基于人工智能的新方法,如专家系统[4]、Tabu搜索[5]、粒子群算法[6,7]、遗传算法[8]和协同进化法[9]等相继引入到电力系统优化问题的研究中,在处理离散变量和寻求全局最优解方面取得了较好的效果。
遗传算法是基于自然界选择原理的一种自适应优化搜索方法,它对计算参数通过二进制编码进行操作,不必考虑求解函数是否可导、可微、线性,从群体出发在整个空间搜索全局最优解,算法具有内在的自组织性、自适应性、自学习性及并行性,给出的结果是离散化的解,符合变压器分接头调整和电容器组投切的实际过程。因此,近年来在电力系统无功优化得到了广泛应用。
文献[10~12]建立了基于遗传算法的电力系统无功优化模型,解决了无功优化中变量的离散和局部最优问题。文献[13]针对遗传算法求解时间过长,引入优化搜索路径的思路,提出了无功功率分层分块优化控制和进化灵敏度分析方法。文献[14]提出一种新型退火选择遗传算法,该算法的收敛速度比简单遗传算法更快。文献[9]将无功优化问题分解为一系列相互联系的子优化问题,每个子优化问题对应于进化算法的一个种群,各种群通过共同的系统模型相互作用,共同进化,从而使整个系统收敛速度提高。文献[15]在自适应遗传算法的基础上引入优良个体池和二次变异操作,增强了算法的局部搜索能力,加快了算法的收敛速度。
电压稳定与无功功率的分布有着紧密的联系。将电压稳定问题引入无功优化,在改善无功潮流分布的同时提高系统的静态电压稳定性。遗传算法具有很强的离散变量处理能力和鲁棒性,但局部寻优能力较差,收敛速度缓慢;模拟退火遗传算法具有较强的全局搜索能力,能有效提高收敛速度;自适应遗传算法在保持群体多样性的同时,能保证遗传算法的收敛能力,有效提高优化能力。本文将自适应遗传算法与模拟退火遗传算法相结合,对遗传算法的基本操作进行改进,并计及静态电压稳定性,使得本文算法在降低网损的同时能够有效提高负荷节点的电压稳定裕度。
1 基于广义Tellegen定理的静态电压稳定裕度指标
n节点电力网络节点电压方程为
(1)
式中:Vpq和Vpv为负荷节点和发电机节点的电压向量;Jpq和Jpv为负荷节点和发电机节点的注入电流向量;Yll和Ygg为负荷节点和发电机节点的自导纳矩阵块;Ylg和Ygl为负荷节点和发电机节点的互导纳矩阵块。
将式(1)化简,消去PV节点,得电力网络方程
YV=DV+J0
(2)
式中:Y是负荷节点的等效导纳矩阵;J0是发电机节点等效的注入电流向量;V是负荷节点电压向量,V=Vpq;D是负荷节点的等效导纳,D=diag(Dii)。
由于电力网络负荷节点为功率注入,因而Dii是任意负荷节点i的等效导纳
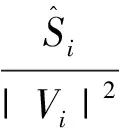
(3)
式中,Si为负荷节点复功率,符号“^”表示共轭。
由广义Tellegen定理,选取式(2)的伴随网络方程
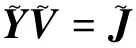
(4)
式中,伴随矩阵为
若考虑第i个节点电压,则取
(5)
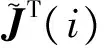
(6)
其中
(7)
因而有
(8)
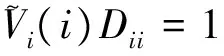
L=|Zii||Dii|
(9)
式中:|Zii|为从i节点向网络内看进去的等效阻抗模;|Dii|为i节点负荷的等效导纳模。如果负荷节点的该指标越小,则说明该节点的电压稳定裕度越大[17]。
2 遗传算法的改进
针对简单遗传算法容易出现早熟,在后期种群同化严重,存在大量相同的个体,导致解的质量较差,收敛速度慢等问题,本文将自适应遗传算法与模拟退火遗传算法相结合,对遗传算法的基本操作进行如下改进。
2.1 适应度函数的改进
遗传算法运行早期个体差异较大,当采用经典的轮盘赌方式选择,后代产生个数与父代个体适应度大小成正比,因此,容易使个别优秀个体的后代充斥整个种群,造成早熟;在遗传算法后期,适应度趋向一致,优秀的个体在产生后代时,优势不明显,从而使整个种群进化停滞不前。因此对适应度适当拉伸是必要的。这样在遗传算法的前期,适应度相近的个体产生的后代概率相近;在遗传算法的后期,拉伸作用加强,适应度相近的个体适应度差异放大,使得优秀个体的优势更明显。
借鉴模拟退火的思想[18],采用的适应度拉伸方法为

(10)
T=T0×0.99t
(11)
式中:F为个体的目标函数值;f为个体的适应度值;t为进化代数;T0为模拟退火的初始温度。
2.2 精英保留策略
为了防止在进化过程中得到的最优个体在以后的进化过程中丢失,精英保留策略是每一代操作结束后都要保留最优个体。具体操作是如果某一代中的一个个体目标函数值小于以往记录的最小目标函数值,则保存该个体;如果这一代个体中没有一个优于以前的最优个体,则用原最优个体替代这一代中的最差个体,并且参与下一代竞争选择。
采用精英保留策略保证了优良个体能遗传到下一代,加快了寻优速度,促进遗传算法的收敛。
2.3 交叉操作的改进
交叉策略采用自适应的交叉概率,使得适应度高的个体采用较小的交叉概率,适应度低的个体采用较高的交叉概率。
(12)
式中:fmax为群体中最大的适应度值;favg为每代群体的平均适应度值;f1为要交叉的两个个体中较大的适应度值。
交叉虽然能够促进基因重组,产生优良个体,但它对原有优良个体的基因破坏作用也相当大。本文采取当选择出来准备交叉的两个个体如果适应度相差很大(当f1≥3f2,f2为要交叉的两个个体中较小的适应度值),则不作交叉,即pc=0,以保证不破坏优良个体的基因,能够顺利地遗传到下一代。
2.4 变异操作
变异策略采用自适应的变异概率,使适应度高的个体采用较小的变异概率,适应度低的个体采用较高的变异概率。
本文采用的编码策略是整数编码,对控制变量编码进行变异操作时,如个体在高位进行一点变异,变异后变量很可能超出范围,使其值被限制在边界上;即使变量不越界,其变化也会较大,造成运行点在解空间“跳跃”,不利于遗传算法的局部搜索。所谓高位低位就是例如本文PV节点电压设了15档,编码是01~15,在进行变异操作时,变异的高位指的是十位,低位指的是个位,显然在实际操作中节点电压都是小范围变化,也就是个位上变化,如果是高位即十位上变化,变化将会很大,详细的意思就是本来编码是02,变异后如果为12,变化就很大,因此本文采用尾部占优原则,就是使变异尽量在编码的尾部即低位进行,更符合实际情况。
3 无功优化的数学模型
电力系统无功优化,是指在给定的运行方式下,将电源的有功出力固定,通过改变发电机/调相机的无功出力(或相应节点电压幅值VG),调节有载调压变压器分接头档位Tij和无功补偿设备投入容量,在满足系统运行的各种约束条件下,使得系统运行的电压质量最高、运行有功网损最小。
为了计及系统的静态电压稳定性,本文采用多目标函数,将负荷节点的电压稳定裕度指标最小(即电压稳定裕度最大)引入目标函数,即
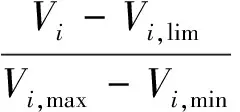
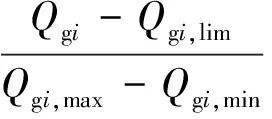
(13)
其中
式中:λV为电压罚系数;λQ为无功罚系数;λL为裕度指标罚系数;PL为潮流计算得到的有功网损;L为电压裕度指标。
等式约束为潮流方程
(14)
式中:PGi和QGi为发电机节点i发出的有功和无功功率;PLi和QLi为负荷节点i的有功和无功负荷;ΔQCi为补偿节点上安装的电容器每档的补偿功率;NCi为补偿节点电容器投入的档数。
不等式约束为
(15)
式中:VGi、NCi、NLi、Tij分别为各发电机的机端电压、补偿电容器的投切组数、补偿电抗器的投切组数、有载调压变压器的调节变比,皆为控制变量;QGi、Sij表示发电机/调相机的无功出力和支路通过功率。
4 无功优化的步骤
步骤1输入原始数据,包括无功控制变量描述和各种约束条件,进行潮流计算。
步骤2根据潮流计算结果,计算系统各个负荷节点的电压稳定裕度指标L,并按照从大到小排序。
步骤3选择L指标较大(即静态电压稳定裕度较小)的前n个节点作为无功补偿点。
步骤4设置遗传算法的操作参数,随机产生一组控制变量,即一组初始解。
步骤5潮流计算,得到各节点的有功、无功、电压和电压稳定裕度指标。
步骤6根据适应函数评价各个个体。
步骤7进行遗传操作,形成新一代个体。
判断是否满足优化条件,若满足优化条件则输出结果,不满足则以新一代个体形成的控制变量去修改上一代数据中相应的部分并返回步骤5。
5 无功优化的步骤
以IEEE30节点系统为例,系统数据参见文献[19],该系统有6个发电机节点(1,2,5,8,11,13),4条变比可调的变压器支路(9-6,10-6,12-4,28-27),共41条线路,其中节点1为平衡节点。PV节点和平衡节点的电压设置为0.90~1.10 p.u.,PQ节点的电压设置为0.95~1.05 p.u.,可调变压器变比的范围为0.90~1.10,发电机无功出力的上下限参见文献[20]。
遗传算法的参数设置,种群规模取20,终止代数为200。简单遗传算法的交叉概率pc为0.6,变异概率pm为0.005;本文算法的交叉概率pc1和pc2分别为0.9和0.6;变异概率pm1和pm2分别为0.1和0.05。λV电压罚系数为15,λQ无功罚系数为5,λL裕度指标罚系数为0.01。
IEEE 30节点系统中节点的静态电压稳定裕度指标L计算结果如表1所示。

表1 节点的静态电压稳定裕度L指标
如前文所述,负荷节点的L指标值越大,表示该节点的电压稳定性越差。选择表中排在前8位的负荷节点,即稳定性较差的8个节点作为无功补偿点。本文所采用的算法对IEEE 30节点系统无功优化的计算结果见表2。
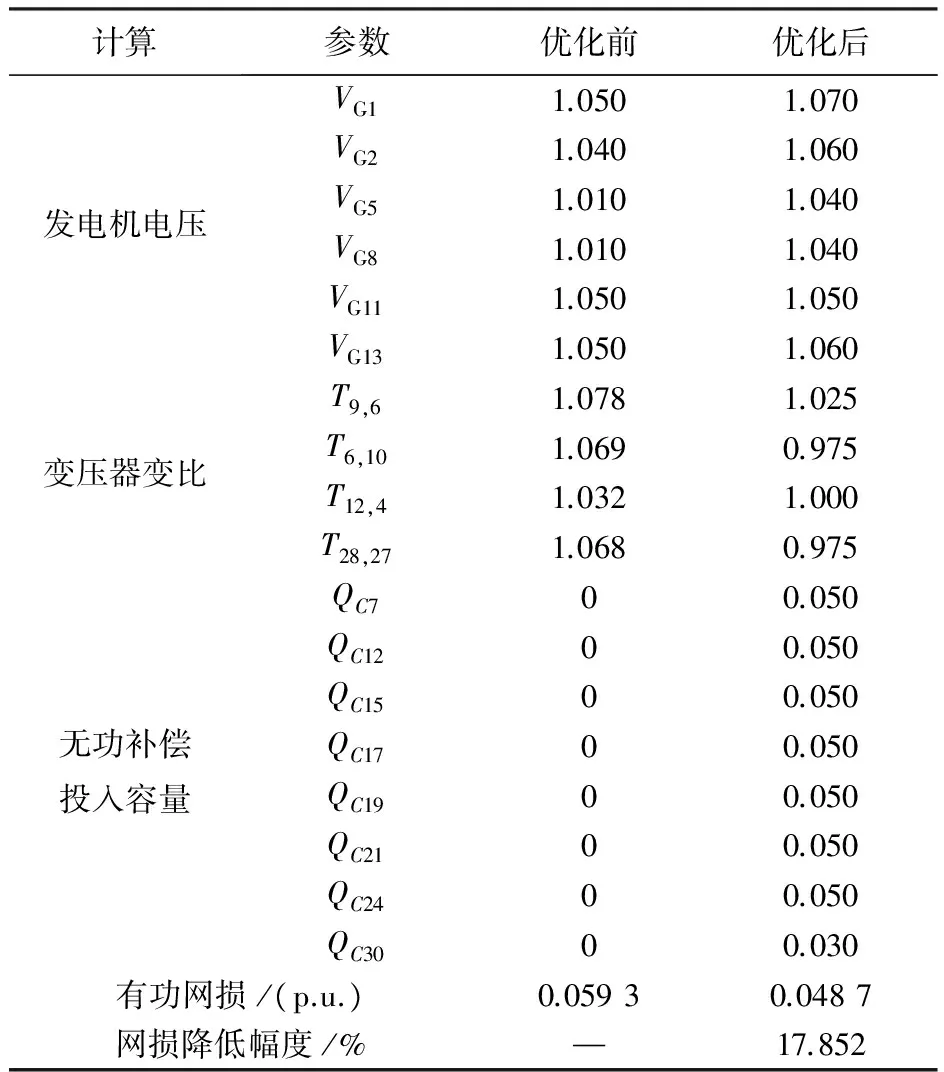
表2 IEEE 30节点系统的优化结果
5.1 网损分析
系统在初始运行状态下的有功网损为5.930 MW,表3为本文算法、改进粒子群算法[6]、协同进化法[9]和简单遗传算法的有功网损。本文算法是随机优化算法随机取20次计算结果,网损平均值为4.870 MW。本文取网损为4.871 MW的结果出来做分析,简单遗传算法随机取20次计算结果,网损的平均值为4.991 MW,本文算法在无功优化后得到的系统网损为4.871 MW,总网损降低了17.852%,与其他几种相比有功网损最小,表明本文提出的方法能够得到更好地最优解。
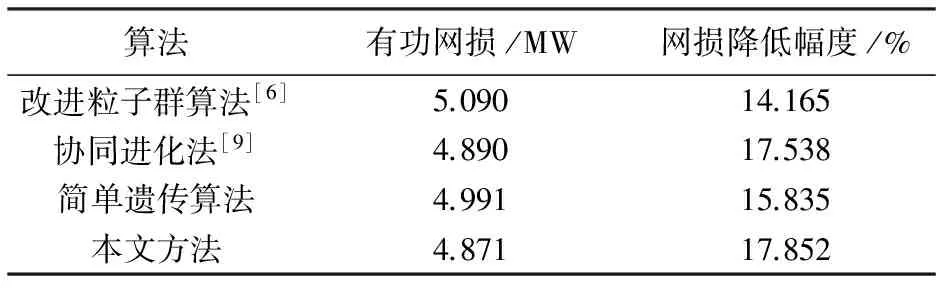
表3 本文方法与其他方法比较
5.2 电压稳定性分析
表4为优化前后节点的L指标,可以看出所选优化节点的L指标有不同程度的减小,电压稳定裕度相应提高,表明本文提出的方法在降低网损的同时能有效提高系统的电压稳定性。
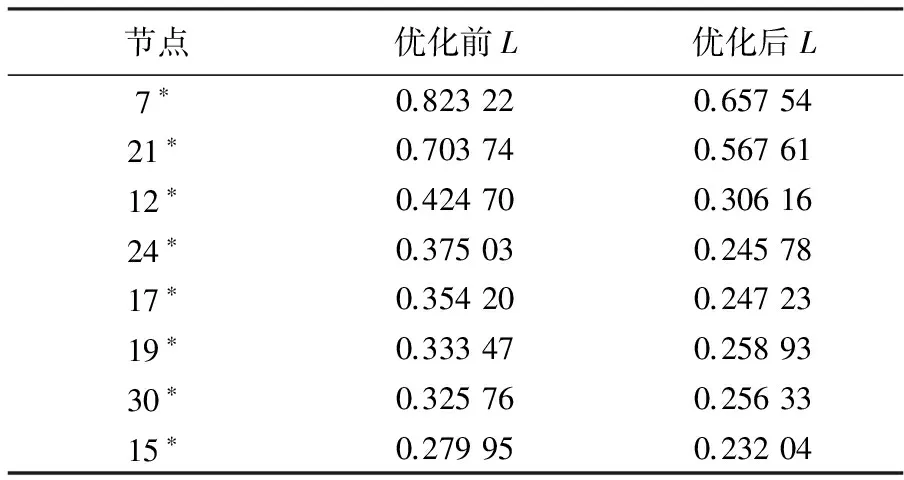
表4 优此前后节点的L指标
图1是优化前后各节点电压值,可以看出优化后各节点电压水平均得到提升,提高了电压品质。
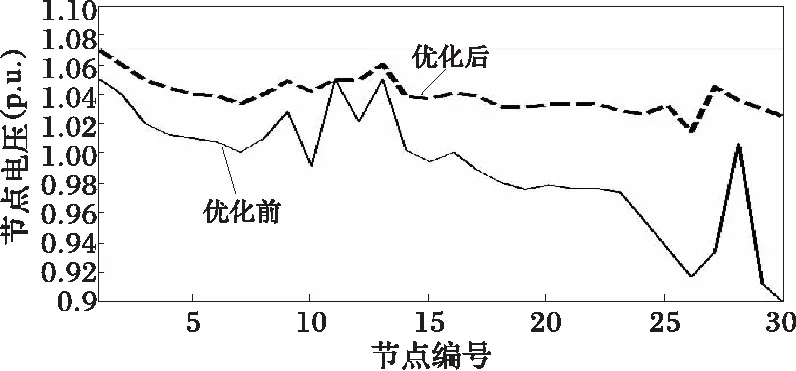
图1 优化前后各节点电压值
5.3 收敛性分析
取本文算法和简单遗传算法的计算结果,做目标函数的收敛曲线如图2所示。结果表明,本文算法比简单遗传算法具有更好的收敛性,而且能更好找到全局最优解。采取改进措施后,从第90代开始,本文算法的目标函数值已降至0.056 0以下,并一直向着优化目标方向搜索,收敛速度明显快于简单遗传算法,且找到的最优解为0.055 754,优于简单遗传算法的最优解0.056 278,从搜索效率和搜索结果看,本文算法比简单遗传算法具有更好的综合性能。
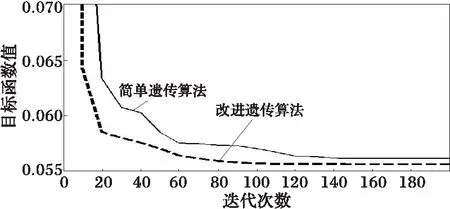
图2 SAGA和GA收敛特性比较
5.4 其他系统优化结果
IEEE14节点系统的初始潮流的有功网损为13.840 MW,随机取20次本文算法的计算结果,平均网损为13.289 MW,网损下降率为3.981%;用本文算法进行优化后L指标最大值由1.758降为1.699,其平均值由0.549降为0.528;电压平均值由1.048升到1.067。
IEEE57节点系统的初始潮流的有功网损为27.859 MW,随机取20次本文算法的计算结果,平均网损为24.138 MW,网损下降率为13.357%;用本文算法进行优化后L指标最大值由0.338降为0.323,其平均值由0.070 5降为0.065 7;电压平均值由0.993升到1.047。
6 结语
本文将节点的静态电压稳定裕度指标最小引入无功优化目标函数,用模拟退火思想对适应度函数改进,用自适应算法对遗传算法的交叉、变异策略进行改进,采用精英保留策略,通过对IEEE14、IEEE30和IEEE57节点系统的无功优化试验研究,将优化结果与简单遗传算法、改进粒子群算法和协同进化算法进行比较,表明本文算法优化结果更优,相对于简单遗传算法有更好地收敛性,加速了算法的收敛速度,在降低网损的同时能够有效提高负荷节点的电压稳定裕度。
[1] 王锡凡.电力系统优化规划[M].北京:水利电力出版社,1990.
[2] 刘明波,李健,吴捷(Liu Mingbo,Li Jian,Wu Jie).求解无功优化的非线性同伦内点法(Nonlinear homogeneous interior-point method for reactive-power optimization )[J].中国电机工程学报(Proceedings of the CSEE), 2002, 22(1): 1-7.
[3] 姚诸香,涂惠亚,徐国禹(Yao Zhuxiang,Tu Huiya,Xu Guoyu).基于灵敏度分析的无功优化潮流(Sensitivity based optimal reactive power flow )[J].电力系统自动化(Automation of Electric Power Systems),1997,21 (11): 19-21.
[4] 颜伟,孙渝江,罗春雷,等(Yan Wei, Sun Yujiang, Luo Chunlei,etal).基于专家经验的进化规划方法及其在无功优化中的应用(EP basing on specialist experiences and its application to var optimization )[J].中国电机工程学报(Proceedings of the CSEE), 2003, 23(7): 76-80.
[5] 王洪章,熊信银,吴耀武(Wang Hongzhang, Xiong Xinyin, Wu Yaowu).基于改进Tabu搜索算法的电力系统无功优化(Power system reactive power optimization based on modified Tabu search algorithm)[J].电网技术(Power System Technology),2002,26(1): 15-18.
[6] 李宏仲,金义雄,程浩忠,等(Li Hongzhong, Jin Yixiong, Cheng Haozhong,etal).基于改进粒子群优化算法并计及静态电压稳定性的电力系统无功规划(Reactive power planning based on improved particle swarm optimization with static voltage stability )[J].电网技术(Power System Technology),2005,29(22):50-55.
[7] 何佳,吴耀武,娄素华,等(He Jia,Wu Yaowu, Lou Suhua,etal). 基于SA-PSO的电力系统无功优化(Power system reactive power optimization based on simulated annealing particle swarm optimization algorithm)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2007,19(5):114-118.
[8] 文劲宇,江振华,姜霞,等(Wen Jinyu, Jiang Zhenhua, Jiang Xia,etal).基于遗传算法的无功优化在鄂州电网中的实现(Genetic algorithm based reactive power optimization and its application in Ezhou city power system )[J].电力系统自动化(Automation of Electric Power Systems),2000,24(2):45-47,60.
[9] 王建学,王锡凡,陈皓勇,等(Wang Jianxue, Wang Xifan, Chen Haoyong,etal).基于协同进化法的电力系统无功优化(Reactive power optimization based on cooperative coevolutionary approach)[J].中国电机工程学报(Proceedings of the CSEE),2004 ,24(9): 124-129.
[10]马晋韬,Lai L L,杨以涵(Ma Jintao,Lai L L, Yang Yihan).遗传算法在电力系统无功优化中的应用(Application of genetic algorithms in reactive power optimization )[J].中国电机工程学报(Proceedings of the CSEE),1995,15(5): 347-353.
[11]程浩忠(Cheng Haozhong).基于遗传算法的电力系统无功优化(Reactive power optimization based on genetic algorithms in electric power systems)[J].上海交通大学学报(Journal of Shanghai Jiao Tong University),1998, 32(1): 127-130.
[12]范宏,韦化(Fan Hong,Wei Hua). 改进遗传算法在无功优化中的应用(Application of improved genetic algorithm in reactive power optimization)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2005,17(1):6-9.
[13]倪炜,单渊达(Ni Wei, Shan Yuanda).具有优化路径的遗传算法应用于电力系统无功优化(A refined genetic algorithm with optimal searching path used in power system reactive power optimization )[J].电力系统自动化(Automation of Electric Power Systems),2000,24 (21): 40-44.
[14]陈皓勇,王锡凡(Chen Haoyong, Wang Xifan).电力系统无功优化的退火选择遗传算法(A genetic algorithm with annealing selection for reactive power optimization )[J].中国电力(Electric Power),1998,31(2): 3-6.
[15]康积涛,钱清泉(Kang Jitao, Qian Qingquan).电力系统无功优化的二次变异遗传算法(Reactive power optimization using second mutation genetic algorithm )[J].电力自动化设备(Electric Power Automation Equipment),2007,27(9):7-11.
[16]徐冰亮,柳焯,王永刚,等(Xu Bingliang,Liu Zhuo,Wang Yonggang,etal).电网负荷节点临界阻抗模的性质及意义(The nature and connotation of the critical impedance module of the load bus in power network )[J].哈尔滨工业大学学报(Journal of Harbin Institute of Technology),1999, 31(4) :91-95.
[17]鲁宝春,王成山,郭志忠,等(Lu Baochun,Wang Chengshan,Guo Zhizhong,etal).基于广义Tellegen定理的静态电压稳定实用判据(A practical method for detecting critical state of voltage stability based on generalized Tellegen's theorem )[J]. 天津大学学报:自然科学与工程技术版(Journal of Tianjin University:Science and Technology), 2001, 34(6) : 727-729.
[18]王小平,曹立明. 遗传算法——理论、应用与软件实现[M].西安:西安交通大学出版社,2002.
[19]Lee K Y, Park Y M, Ortiz J L. A united approach to optimal real and reactive power dispatch[J]. IEEE Trans on Power Apparatus and Systems, 1985,104(5):1147-1153.
[20]张伯明,陈寿孙,严正.高等电力网络分析[M].北京:清华大学出版社,2007.
Multi-objectiveReactivePowerOptimizationwithStaticValtageStability
YANG Xiao-ping1, ZHANG Qiang2, XUE Bin1, WANG Lei3
(1.Faculty of Water Resources and Hydraulic Power, Xi'an University of Technology, Xi'an 710048, China; 2.Foshan Electric Power Design Institute Company Limited, Foshan 528200, China; 3.Northwest Electric Power Design Institute, Xi'an 710075, China)
The genetic algorithm has three disadvantages:early maturity,poor ability of local optimization,and slow convergence rate.In order to overcome these problems,some modified methods of reactive power optimization to improve the static voltage stability of power system were proposed.In this paper,fitness function was modified by using simulated annealing theory.Genetic algorithm crossover and mutation strategy were improved by using adaptive algorithm.The tactics of elites to keep and mutation operation used tail-prevailing principle were adopted.The minimization of voltage stability margin index based on the generalized Tellegen's theorem was taken as one of objective functions.Compared with the other methods on IEEE 14-bus,IEEE 30-bus and IEEE 57-bus system,the optimization results show that the proposed algorithm optimization has better convergence property than simple genetic algorithm,which accelerated the algorithm convergence speed,and effectively improve the voltage stability margin of load buses while reducing the power loss.
power system; reactive power optimization; static voltage stability; margin index; modified genetic algorithm
2009-05-11
2009-10-09
TM714.3
A
1003-8930(2011)01-0138-07
杨晓萍(1964-),女,副教授,研究方向为电力系统运行与控制。Email:yangxiaoping@xaut.edu.cn 张 强(1985-),男,硕士研究生,研究方向为电力系统运行与控制。Email:81867897@qq.com 薛 斌(1982-),男,硕士研究生,研究方向为电力系统运行与控制。Email:xueb@nw.sgcc.com.cn

