基于EMD和相关向量机的短期负荷预测①

孙志刚， 翟玮星， 李伟伦， 卫志农

(1.南通供电公司， 南通 226006； 2.河海大学能源与电气学院， 南京 210098)

基于EMD和相关向量机的短期负荷预测①

孙志刚1， 翟玮星2， 李伟伦1， 卫志农2

(1.南通供电公司， 南通 226006； 2.河海大学能源与电气学院， 南京 210098)

为提高电力负荷预测的准确性，提出一种基于经验模态分解EMD(empirical mode decomposition)与相关向量机RVM(relevant vector machine)的短期负荷预测方法。该方法利用EMD将目标负荷序列分解为若干个不同频率的固有模态分量IMF(intrinsic mode function)，通过分析各个分量的特征规律，构造不同的RVM模型对各分量分别进行预测，再将各分量预测值通过RVM组合得到最终预测值。仿真结果表明，通过EMD分解，预测效果有显著改善，而RVM模型较之BP神经网络模型与SVM模型具有更高的预测精度。

经验模态分解； 相关向量机； 固有模态分量； 短期负荷预测

电力负荷预测是电力系统调度、用电、计划、规划等管理部门的重要工作之一[1]。短期负荷预测是负荷预测的重要组成部分，它对于机组最优组合、经济调度、最优潮流、电力市场交易等都有着重要的意义。负荷预测精度越高，越有利于提高发电设备的利用率和经济调度的有效性[2]。

短期负荷预测的研究已有很长历史，国内外的许多专家、学者在预测理论和方法方面作了大量的研究工作，取得了卓有成效的进展[2]。现有的预测方法主要有时间序列法[3]、人工神经网络法[4]、支持向量机法[5]及小波分析法[6]等。而其中的小波分析法是通过小波变换，将负荷分解到不同的尺度频率分量上，然后根据各个尺度上负荷波动的方式，选用不同的预测方法进行预测。

由于小波变换的变尺度分析能力及对局部时间区间信息的“显微”能力，使其在负荷预测及电力系统其他方面的研究中都有广泛的应用。但是小波变换本质上是窗口可调的傅里叶变换，它并没有摆脱傅里叶分析的局限，不能用于处理非线性问题，且在计算过程中需要人为地选择小波基和分解尺度，主观因素对分解结果影响较大。

鉴于此，本文应用了一种新的时频分析方法，即经验模态分解(EMD)方法[7]，该方法是由Huang在1998年提出的Hilbert-Huang变换中的核心部分。EMD本质上是对一个信号进行平稳化处理，其结果是将信号中不同尺度的波动或趋势逐级分解开来，产生一系列具有不同特征尺度的数据序列，每一个序列即为一个IMF分量[8]。EMD方法较之小波变换及其他信号处理方法都有更高的分辨率及很强的非线性处理能力，因此越来越多地引起国内外学者的关注和研究[8,9]。

由于负荷的随机因素太多，非线性极强，通过EMD分解可以得到平稳的IMF分量。对各分量进行分析研究，就可以选择合适的预测模型进行分别预测。文献[10]采用支持向量机SVM(support vector machine)对各IMF分量进行分别预测，然后将各分量预测值输入到新的SVM中得到最终的预测值。文献[11]则采用相匹配的BP(back propagation)神经网络分别预测，然后通过自适应线性神经网络组合得到最终的预测值。

相关向量机(RVM)是由Tipping提出的基于总体贝叶斯框架下的稀疏概率模型，是近来机器学习领域的研究热点之一。相关向量机不仅拥有支持相量机(SVM)的工作性能，同时具有一些SVM所不具备的优点，如RVM的核函数K不必满足Mercer条件；RVM在权系数之上引进了超参数，从而大大降低了计算的复杂度等。

因此，本文尝试用RVM对EMD分解得到的各IMF分量分别进行预测，然后再用RVM将所有分量预测结果组合得到最终的预测值。算例结果表明，基于该方法的短期负荷预测可以有效的提高预测精度。

1 理论基础

1.1 经验模态分解方法

首先对固有模态函数(IMF)做一个简要描述。直观上，固有模态函数具有相同的极值点和过零点数目，且都对称的服从于局部零均值。一个固有模态函数必须满足以下两个条件：一是在整个数据序列中，极值点的个数与过零点的个数必须相等或最多相差不多于一个；二是在任意时刻点，由极大值点定义的上包络线和由极小值点定义的下包络线的平均值为零[7]。基于以上对IMF的定义，EMD分解算法如下[7]。

步骤1确定待处理序列x(t)的所有极大值点序列和极小值点序列。用三次样条插值方法分别拟合极大值序列与极小值序列，得到x(t)的上包络线vmax(t)和下包络线vmin(t)。

步骤2求出上下包络线的均值包络线m1(t)，即

(1)

并计算x(t)与m1(t)之差

h1(t)=x(t)-m1(t)

(2)

步骤3判断h1(t)是否满足IMF的两个条件，若满足，则h1(t)为第一个IMF；若不满足，则将h1(t)视为新的待处理序列，重复步骤1和步骤2k次，得到

h1k=h1(k-1)-m1k

(3)

使得h1k(t)满足IMF的条件，记c1(t)=h1k(t)，则c1(t)为x(t)的第一个IMF。

步骤4将r1(t)=x(t)-c1(t)作为新的待处理序列，重复以上步骤，得到n个IMF，当r(t)变成常数或单调函数，不能再从中提取满足IMF的分量时，分解过程结束。这样原始序列x(t)就可以表示为

(4)

1.2 相关向量机预测方法

支持向量机在电力系统负荷预测中已经得到了较为成功的应用，但也存在不足之处，主要表现在其支持向量个数仍显较多，这一方面可能造成过拟合，另一方面则增加了计算时间；SVM的核函数必须满足Mercer条件，且惩罚因子需要人为设定，其对结果有很大影响。这些不足使得支持向量机在实际应用中仍受到一定限制。相关向量机作为总体贝叶斯框架下的概率模型，正好能弥补这些不足，这对于实际问题的解决是有很大帮助的。以下简要介绍RVM的基本理论[12]。

(5)

式中：w为权参数向量，w=(w0，w1，…，wN)；ξn为独立同分布的零均值高斯噪声，其方差为σ2；φi(x)为非线性基函数，φi(x)≡K(x，xi)，K(·)为核函数。

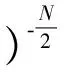
(6)

式中：t=(t1，…，tN)T；Φ=[φ(x1)，φ(x2)，…，φ(xN)]T，φ(xN)=[1，K(xn，x1)，K(xn，x2)，…，K(xn，xN)]T。

由于模型中存在较多参数，采用最大似然估计由式(6)得到的w和σ2容易导致过拟合，为此，采用稀疏贝叶斯原理对w赋予零均值高斯先验分布得

(7)

其中α为N+1维超参数向量。这样，每一个权重就单独地对应一个超参数，从而控制先验分布对各参数的影响，以确保相关向量模型的稀疏性。

以上在定义了先验概率分布及似然分布以后，根据贝叶斯原理，就可以求得所有未知参数的后验概率分布为

exp{-(w-μ)TΣ-1(w-μ)}

(8)

其中，后验协方差矩阵为

Σ=(σ-2ΦTΦ+A)-1

μ=σ-2ΣΦTt

A=diag(α0，α1，…，αN)

为了确定模型权值，首先需要得出超参数的最佳值，可以通过迭代算法求得，即

(9)

(10)

式中：μi为第i个后验平均权；Nii为后验协方差矩阵第i个对角元素；N为样本数据个数。

若给定新的输入值x，则相应输出的概率分布服从高斯分布，即

(11)

其中的预测均值为y*=μTφ(x*)，则y*即可作为t*的预测值。

2 基于EMD与RVM的短期负荷预测

2.1 负荷序列的经验模态分解与分析

2.1.1 负荷序列分解

电力系统负荷序列是一种典型的具有周期性、随机性和趋势性的非平稳时间序列，通过EMD分解，可以得到若干个不同频率的平稳的IMF，从这些若干个不同的IMF可以更明显地看出原负荷序列的周期性、随机性和趋势性。文献[13]通过对日用电量进行经验模态分解，来挖掘负荷特性及因素的影响作用。本文则试图对连续日的负荷曲线进行分解分析，以求得到其内在的固有特性。

图1为某地区2009年夏季8月1日到8月15日连续15 d(小时负荷曲线)共360个数据点的负荷序列及其分解得到的IMF分量及余项。由图可以看出该地区电力系统负荷序列经EMD分解后自适应地解析出5个IMF分量和一个趋势项，所有的IMF按从高频到低频的顺序排列。

图1 原始负荷及EMD分解分量

2.1.2 各IMF特征分析

为了对各IMF建立有效的预测模型，本文主要从周期性及与温度的相关性方面分析各IMF的不同特征。与文献[13]相同，本文也采用文献[14]提供的方法计算各IMF的平均周期。温度指标一般为日最大、最小、平均温度，与小时负荷对应的逐时温度变化数据较难获得，因此本文将上述15 d的IMF分量仍然按天排列，并选取同一时刻不同日的各IMF分量与日最大温度、日最小温度、日平均温度进行相关性分析。分析结果如表1所示。

表1 各IMF特性分析表

对于周期性分析，由表1的计算结果，IMF1的平均周期约为5 h，这与一天内工作时间与休息时间用电规律差异有关，反映了该分量在一天内的波动情况，但其规律性不明显，具有一定的随机性；IMF2的平均周期为12 h，反映了由于生活生产规律所引起的用电差异，该分量已具有较为明显的周期性；IMF3～IMF5的周期幅度较大，分别为一天、一周和两周，它们波动平滑，周期性明显，反映了以天为单位的负荷的周期性变化。余项则反映了负荷序列的整体走向。

与温度的相关性分析，由表1可以看出，温度指标中日最高温度与各分量的相关性最强，这说明夏季最高温度对负荷的影响较为明显。而日最高温度又与IMF1和IMF2的相关性最强。这是由于IMF1和IMF2反映的都是负荷在一天内的变化特性，这种一天内的负荷变化会受到温度的影响。IMF3-IMF5及余项与温度的相关性相对较低，这说明负荷较为规律的周期性变化受温度的影响较小。当然不同时刻点的IMF分量与温度的相关系数不尽相同，但表征的相关性程度都是一致的。

2.2RVM预测模型的建立

2.2.1 RVM模型输入变量的确定

RVM预测模型采用多输入、单输出的一步预测方法对一天24点负荷分别建立模型进行预测。

根据各IMF分量的不同特性，选择适合各分量的输入变量建立预测模型，可以有效提高预测精度。依据第2.1节中对各分解分量的分析，表2列出了各个分量预测模型的输入变量。其中y(t，d)表示预测第d天第t时刻的负荷，x的表示含义与y类似，T(d)表示第d天的最高温度，D表示第d天的日类型。

表2 各分量预测模型的输入变量

对于随机分量，其平均周期为5 h，因此输入变量中包含预测日前一天的前5 h负荷数据。对于节假日，可以选择上一个节假日对应的前5 h的负荷，由于随机分量反映的是一天内负荷的变化情况，其受到温度及日类型的影响，因此输入变量中亦包含预测日的日最高温度及日类型。

周期分量IMF2既反映了负荷在一天内的变化规律，又包含较为清晰的周期性，且与温度及日类型的相关性较强，因此输入变量中即包含与预测时刻相领近的负荷点(为方便起见，仍选择前5 h的负荷)，又包含相同时刻不同日的负荷和日最高温度及日类型。周期分量IMF3～IMF5的周期性较为明显，都是以一天为最小单位周期变化，因此输入变量选择连续7 d同一时刻的负荷数据。

余项的趋势性较为显著，因此输入变量选择连续多日的相同时刻负荷数据即可，本文选择连续10 d对应时刻点的数据。

2.2.2 RVM模型参变量的确定

本文选用径向基RBF(radial basis function)核函数作为RVM模型的核函数。而RVM预测模型中超参数α通过训练可以自适应得到最优值，无需人为确定，但是为了保证RVM模型的最优性，核函数的宽度δ2的确定至关重要，因此为了避免人为确定带来的主观性，本文采用遗传算法来分别获得每个RVM模型的最优参数值，选取平均绝对百分误差MAPE(mean absolute percentage error)作为算法的评价函数，其计算式为

(12)

2.3 基于EMD与RVM的短期负荷预测模型

通过以上EMD分解及RVM预测模型的建立，可以得到本文所提的基于EMD-RVM的短期负荷预测模型，如图2所示。

图2 EMD-RVM短期负荷预测模型

3 算例分析

为了验证算法的有效性，本文以江苏省南通市2009年5月1日～8月6日的负荷数据及气温、日类型作为训练样本，预测8月7日全天24点的负荷值。预测误差采用如式(12)的平均绝对百分比误差MAPE。

本文采用BP神经网络方法、SVM方法及RVM方法对未分解的原始负荷序列及经过分解后的负荷序列分别建立预测模型，预测MAPE如表3所示，为便于观察，图3仅画出RVM及EMD-RVM模型的预测结果。由表3可以看出，对于未进行分解的情况，机器学习方法的预测效果明显好于神经网络方法。在机器学习方法中，RVM的预测效果也要好于SVM，且通过统计，SVM模型中支持向量的个数为63个，而RVM模型中相关向量的个数仅为19个，RVM模型更加稀疏。经过EMD分解后，各方法的预测精度均有不同程度的提高，分别为0.71%、0.65%和0.83%，其中EMD-RVM提高的幅度也略为占优。图3能够清晰地显示经过EMD分解后预测效果的改善情况，特别对于负荷极大值及附近的时刻点，EMD-RVM模型能够更好地反映负荷局部特征，提高预测精度。

表3各预测模型的MAPE

Tab.3MAPEofeachmodel%

模型未分解EMD分解BP3．282．57SVM2．461．81RVM2．091．32

图3 RVM及EMD-RVM预测结果

4 结语

本文提出了基于经验模态分解与相关向量机的短期负荷预测模型。利用EMD自适应地将非平稳的负荷序列分解为不同尺度的IMF分量，根据各分量的不同特征，分别建立RVM模型进行预测，最后再用RVM对分量预测结果进行组合得到最终的预测结果，仿真结果表明，RVM模型较之BP神经网络与SVM模型，预测精度有较为明显提高，且模型更为稀疏。而通过EMD分解后，各方法的预测精度能够进一步提高，且EMD-RVM提高的幅度也更大。

[1] 牛东晓，曹树华，卢建昌，等.电力负荷预测技术及其应用[M].2版.北京：中国电力出版社，2009.

[2] 康重庆，夏清，刘梅.电力系统负荷预测[M].北京：中国电力出版社，2007.

[3] Yang Hong-Tzer, Huang Chao-Ming. New short-term load forecasting approach using self-organizing fuzzy ARMAX models[J].IEEE Trans on Power Systems,1998,13(1):217-225.

[4] 李林川，夏道止，杨振平，等(Li Linchuan, Xia Daozhi, Yang Zhenping,etal). 应用人工神经网络进行短期负荷预测(Short-term load forecasting using artificial neural network)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，1994，6(3)：33-41.

[5] 李云飞，黄彦全，蒋功连(Li Yunfei, Huang Yanquan, Jiang Gonglian).基于PCA-SVM的电力系统短期负荷预测(Short-term load forecasting based on PCA-SVM)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2007，19(5)：66-70.

[6] 宋超，黄民翔，叶剑斌(Song Chao, Huang Mingxiang, Ye Jianbin).小波分析方法在电力系统短期负荷预测中的应用(The application and problems of wavelets used in short-term power load forecasting)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2002，14(3)：8-12.

[7] Huang N E, Shen Z, Long S R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].The Royal Society, 1998, (454):903-995.

[8] 高磊(Gao Lei).HHT理论在电力系统中的应用研究(Research on the Application of HHT Theory to Power System)[D]. 吉林：东北电力大学电气工程学院(Jilin: School，Electrical Engineering of Northeast Dianli University)，2006.

[9] Robertson H J, Soraghan J J,Idzikowski C,etal. EMD and PCA for the prediction of sleep apnoea: a comparative study[C]∥IEEE International Symposium on Signal Processing and Information Technology, Cairo, Egypt: 2007.

[10]祝志慧，孙云莲，季宇(Zhu Zhihui, Sun Yunlian, Ji Yu).基于EMD和SVM的短期负荷预测(Short-term load forecasting based on EMD and SVM)[J].高电压技术(High Voltage Engineering)，2007，33(5)：118-122.

[11]郑艳秋(Zheng Yanqiu).基于经验模式分解和神经网络的短期电力负荷预测方法研究(Research on Short-Term Power Load Forecasting Based on Empirical Mode Decomposition and Artificial Neural Network)[D].重庆：重庆大学电气工程学院(Chongqing: College of Electrical Engineering，Chongqing University)，2009.

[12]Tipping M E. Sparse Bayesian learning and the relevance vector machine[J].Journal of Machine Learning Research ，2001，1(3)：211-244.

[13]牛东晓，李媛媛，乞建勋，等(Niu Dongxiao, Li Yuanyuan, Qi Jianxun,etal).基于经验模式分解与因素影响的负荷分析方法(A novel approach for load analysis based on empirical mode decomposition and influencing factors)[J].中国电机工程学报(Proceedings of the CSEE)，2008，28(16)：96-102.

[14]梁强，范英，魏一鸣(Liang Qiang, Fan Ying, Wei Yiming).基于小波分析的石油价格长期趋势预测方法及其实证研究(A long-term trend forecasting approach for oil price based on wavelet analysis)[J].中国管理科学(Chinese Journal of Management Science)，2005，13(1)：30-36.

Short-TermLoadForecastingBasedonEMDandRVM

SUN Zhi-gang1， ZHAI Wei-xing2， LI Wei-lun1， WEI Zhi-nong2

(1.Nantong Power Supply Company,Nantong 226006, China; 2.School of Energy and Electrical, Hohai University, Nanjing 210098, China)

In order to improve the accuracy of power system load forecasting,a load forecasting model based on empirical mode decomposition(EMD)and relevant vector machine(RVM)is proposed.Using the EMD,this method decomposed the target load sequence into a number of different frequency components of the intrinsic mode function(IMF).By analyzing the characteristics of various components of the law,different models to forecast each component separately were consturcted using RVM,and then these forecasting results of each IMF are combined with RVM to obtain final forecasting result.The simulation results show that the predictive validity based on decomposition by EMD has been improved significantly,and RVM method has higher precision and greater generalization ability than SVM method and the BP neural network method.

empirical mode decomposition(EMD)； relevant vector machine(RVM)； intrinsic mode function(IMF)； short-term load forecasting

2010-04-15

2010-08-30

TM715

A

1003-8930(2011)01-0092-06

孙志刚(1977-)，男，工程师，研究方向为电网规划。Email:szg2035@sina.com 翟玮星(1985-)，男，硕士研究生，研究方向为电力系统负荷预测。Email:zwx-zwx1985@tom.com 李伟伦(1977-)，男，工程师，研究方向为电网规划。Email:lwl267@hotmail.com 卫志农(1962-)，男，博士，教授，博士生导师，研究方向为电力系统运行、分析与控制和输配电自动化等。Email:wzn_nj@263.net