演化电力市场的古诺调节分析①

游义刚， 周晓阳

(1.华中科技大学水电与数字化工程学院， 武汉 430074； 2.华中科技大学数学与统计学院， 武汉 430074)

演化电力市场的古诺调节分析①

游义刚1， 周晓阳2

(1.华中科技大学水电与数字化工程学院， 武汉 430074； 2.华中科技大学数学与统计学院， 武汉 430074)

根据复杂适应系统的自动机网络建模方法，对电力市场稳定性问题进行整体性研究。建立了实验电力市场自动机网络模型一般框架：以发电商和ISO作为底层单元、以市场竞价规则作为演化机制。对优化定价模型进行博弈分析，并设计了渐进式古诺调节模式。针对典型案例，观察到渐进式古诺调节过程的特征，归纳推理出市场力在一系列负荷临界值可能具有爆发性释放的特点，这导致市场价格在这些临界点呈跳跃状增加。通过案例实验追踪演化历程，揭示导致电力市场失稳的可能成因。

电力市场； 自动机网络建模； 演化博弈； 古诺调节； 市场力

电力市场稳定性是能源安全战略中的重要问题。目前，对电力市场稳定性的研究方法[1]都局限于：①电价在均衡点附近的小扰动；②线性化模型；③特征值分析；④不考虑扰动强度和扰动持续时间的影响；⑤不考虑可用发电容量的变化；⑥不考虑投资市场对交易市场的影响；⑦不考虑参与者的博奕策略；⑧不考虑电网阻塞；⑨定性研究。文献[2]力图突破经典方法的瓶颈，基于市场经济规律，结合电力生产、交易和电力系统运行的特点，建立了电力市场的框架模型，倡导用实验电力市场方法探索电力市场和电力系统的内在规律。文献[3]对发电商的微观行为进行深入分析，证明了市场的信息结构对发电商的报价策略的选择和市场力的发挥，均起着重要作用。

电力市场是一个既具有社会经济学的特征、也具有极强的物理背景的大规模复杂系统。面对这样的复杂系统，经典的研究方法显得力不从心。为深入研究造成电力市场不稳定的内在原因，选择了自动机网络方法。自动机网络方法[4]是在复杂系统的研究基础上概括总结的分析复杂系统的一套方法，它将复杂系统抽象成一些相互连接的自动机(称之为单元)，该方法具有如下特点：①不认为在了解系统的宏观行为时，每个单元的细节是重要的；②认为主要是单元的数目，即系统的规模对系统的宏观特性有决定性的影响；③着重于观察与研究系统的宏观特性。自动机网络方法本身只是一个框架，模型的有效性依赖于演化规则的设计。

在开放电力市场中，博弈论是研究和理解竞争行为的重要工具之一。经典博弈模型[5]以讨论均衡点为主，然而在电力市场中，基于某些因素，即使均衡点的存在，也不能保证参与者在实践中可以达到均衡态。同时均衡点可能不唯一：如果存在多个均衡，实际中往往缺乏明显证据分辨哪一个均衡点将是市场可以到达的。博弈学习理论[6]引进了学习机制，将博弈论的研究重点转变为系统将如何到达均衡。古诺调节就是这些学习机制的一种。

根据复杂系统自动机网络方法，可对电力市场进行建模[7～9]：成本、最大供应量、报价函数构成发电商的基本要素；需求曲线、ISO(independent system operator)的定价规则决定了发电商的基本生存条件；定价规则不变的假定固定了发电商和ISO的相互作用模式，于是剩下的问题是确定发电商之间的相互作用模式或演化机制。复杂系统自动机网络建模方法将博弈学习规则理解为发电商在适当的信息结构下相互作用的演化机制。这样，不同博弈学习规则就对应于不同的自动机网络模型，古诺调节只是一种特殊的自动机网络模型。

本文拟用复杂系统的自动机网络建模方法，通过对造成电力市场不稳定原因分析，探索电力市场的内在规律。文中对优化定价模型进行博弈分析，并设计了渐进式古诺调节模式。最后结合典型案例运用古诺调节进行模拟，揭示导致电力市场失稳的可能成因。

1 建模和演化规则

用自动机网络方法建立实验电力市场模型，首先要根据问题的背景确定底层单元(自动机)。例如在统一出清价环境下的单边开放电力市场，如不考虑电网约束，发电商或机组就构成了底层单元。如果在模型中要考察独立系统调度人(ISO)的行为改变对发电商生存环境的影响，则底层单元可由发电商、ISO构成。类似的，可将电力批发商、用户等单元加入其中一步步扩展模型。

在确定底层单元以后，需要建立自动机相互联接机制或演化规则。电力市场具有很强的物理和技术约束，这些约束使底层单元的联接结较为复杂，这与一些其他的复杂系统的研究有所不同，且演化机制必须遵循电力市场的物理背景。本文重点考虑需求为低弹性的单边开放电力市场。模型中，发电商和ISO构成底层单元。最基本的演化机制为发电商的报价策略和ISO的定价方法。值得注意的是，演化机制可能是相当多的。随着时间的推移，电力市场的各底层单元为追求自身效用的最大化会不断创新演化机制。

系统相对于底层单元构成整体，市场的稳定性一定是整体行为，仅对单个发电商的报价策略追踪是无法确定市场是否稳定的。假定环境不变，底层单元会按照电力市场固有的规律相互作用，在长期演化中会逐渐找到自己应有的位置。因此，了解系统的演化趋势对维护电力市场的稳定性是极为重要的。

在电力市场的自动机网络建模中，统一出清定价模型被视为一种演化机制，该机制刻画了底层单元ISO和发电商、发电商和发电商之间的内作用。理论上，可以有多个定价模型，每一种定价规则均可视为ISO的策略，从这一观点出发，电力市场中的博弈行为不仅仅只在发电商之间展开，ISO也是局中人之一。ISO的不同策略对发电商构成不同的激励，或者为发电商提供了不同的生存环境。从电力市场稳定性地位来看，应当研究何种策略会产生较大的市场风险，何种策略可有效的抑制电力市场的不稳定。

2 优化定价模型

为深入展开对电力市场的研究，首先建立一个计算稳定且可靠的定价算法作为基本保障。在电力市场中，发电商的报价必须基于交易中心的电力交易决策模型和算法。本文假设电力市场由N个独立的发电商组成，ISO根据各发电商的报价决定市场电价。在单边开放发电侧市场的情形下，ISO的优化目标为购电费用最小，约束条件可分为功率和容量、时间、电网安全等，从而可得到优化定价模型。相比市场供应函数模型，优化定价模型有较好的可扩展性。例如，为简化问题，可以先考虑功率和容量约束的优化定价问题，然后逐步添加其他约束，这至少在模型的表述上没有任何困难，只是求解技术难度增加而可靠性降低。

本文假设市场为低负荷弹性，即r≈0。如果仅考虑负荷平衡和发电容量限制约束[10]，则电力市场单时段统一出清价的定价模型为

minq1，q2，…，qk{max{λ1(q1)，λ2(q2)，…，

λk(qk)}}Q

(1)

式中：qi为发电商i的出力；λi(qi)为发电商i报价函数，设λi(·)是严格单调递增的连续函数。

根据约束条件，由模型确定的出清价将不低于所有发电商的最低报价λi=λ(qi)。如果定价规则为接纳全体发电商，则发电商肆意抬价将成为不可避免。因此ISO应采用在可能的情形下删除高报价发电商的规则，这时取代公式(1)的模型为

λk(qk)·xk}}

(2)

(3)

即ISO可在K个发电商中选择部分发电商并完全接受它们的报价，从而在低负荷时可排除了报价过高的发电商。

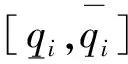
(4)

注意到当市场价格低于低限报价λi时，发电商i将被排除在市场之外，不向系统供电。所以其供应函数应为

(5)

3 渐进式古诺调节

电力市场可以简单看作一个寡头市场，例如在发电市场中，可以认为各发电商的电力商品是同质的，在不考虑电网技术约束的前提下，可建立发电商的古诺模型。假定电力市场有K个发电商，发电商i的二次成本函数为

总之，与现浇结构的分析相比，装配式结构的优点显而易见，不仅减少了施工量，降低了人工成本，而且还可以在很大程度上节省原材料，降低施工噪声，粉尘污染，建筑垃圾和合理的污水排放，对节能环保十分有利，目前我国应用建筑工业化一直处于起步阶段。如果我们国家要实施大规模的工业化建设，就要积极开展相应的研究，结构关键技术。

(6)

若发电商i采用其边际成本的倍数进行报价，即

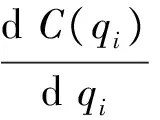
(7)

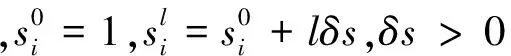
根据电力市场的优化定价模型可知

qi=qi(λ)=βi(si)λ+αi

(8)

因此，发电商i的供应函数为

(9)

同理可知，发电商i的利润函数为

ui=λqi-Ci(qi)

(10)

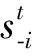
(11)

(12)

4 案例分析

本文以标准的IEEE 6机30节点系统为例，对以上模型进行案例仿真和分析。假设6台发电机组分别属于6个不同的发电商，其生产成本参数如表1所示，其中a、b、c为发电商二次成本函数的系数。

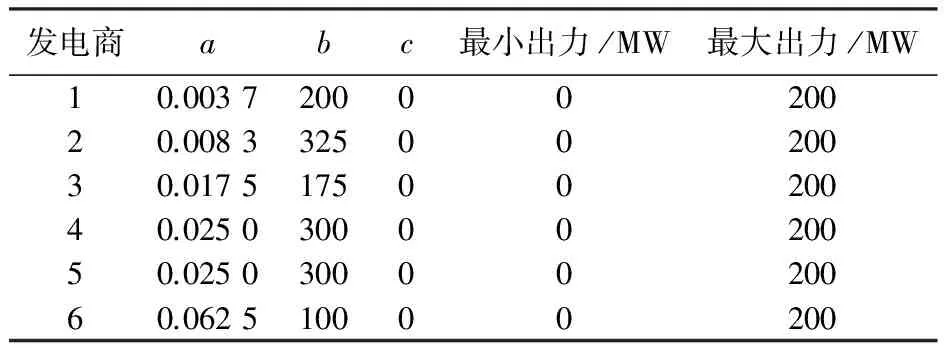
表1 发电商成本系数

由计算结果，可以给出各发电商按边际成本报价的系统成本曲线和古诺调节价格曲线，如图1所示：在低负荷时(Q≤ 200，即小于单厂总供给)边际成本价与古诺调节价重合，这说明供给远大于需求时，发电商处于完全竞争状态。随着需求增加，古诺调节价偏离边际成本价、逐步攀升，并呈现出跳跃式增长。跳跃点多出现在单厂总供给的倍数附近，如400、800和1 000。这意味着，诸发电商合成的市场力随着负荷增加而增加，且在古诺调节的演化机制下，在某些临界点处会对市场价格构成跳跃式的冲击，这种冲击在五倍单厂总供给(1 000 MW)附近显得更加明显。当价格在Q=726.05、736.13 MW处出现二周期态的不收敛点，由于发电商2、3通过抬高报价策略实现容量持有，从而导致高价格，但这时其他发电商尚有调节最优的余地，牵制2、3重新返回低报价策略使得市场价格回到低价位，因而价格在两个状态之间反复切换而不能收敛。当需求接近200×5 MW，收敛开始变得困难起来，收敛前的振荡期越来越长，价格波动幅度大，无规律可寻，处于一片混沌无序状态。随着迭代时间的增加，价格突然进入有序状态：或者收敛，或者趋向无穷。

图1 古诺调节价格和边际成本价格

图1中，成本价格指发电商按边际成本报价所得出清价；渐进式指按渐进式古诺调节出清价(Li=20)。因价格数据差异过大，分为两个子图分别显示，且用180代表+∞

在以上案例实验中，每一发电商最大出力(称为单厂总供给)都是相同的。市场力是负荷的函数，并会随着负荷需求的增加逐步得到释放，当负荷达到某个门限值时，市场力可能会因为发电商事实上已达到的某种策略默契突然增加释放速度，导致电价大幅上扬。当发电商意识到抬高市场价格可获得更大的利润，且自己处于寡头市场，拥有一定的抬高市场价格能力。然而在演化过程中，各发电商为寻求与自身实力相匹配的市场地位将与其它发电商进行“策略碰撞”，如果这种碰撞是以非合作方式进行(非合作竞争)，这将损耗发电商的部分市场(分)力。随着演化时间的推进，发电商可能都达到了与自身实力相匹配的市场位置，这时碰撞停止，市场合力形成，价格将进入均衡态；但也可能出现全体或部分发电商无法停止碰撞的局面。如果全体或部分发电商不是进行策略碰撞，而是通过合作、共谋或策略默契合成更强的市场力，则电力市场必将是不稳定的。

5 结语

在寡头市场中，每个处在寡头地位的发电商都拥有一定的市场分力，这些市场分力的合成形成了(总)市场力。电力市场稳定与否和风险大小既与个体发电商的市场分力强度有关，也与这些分力方向有关。需求是市场力的开关因子之一。在完全信息的古诺调节模式下，市场力随着需求增加而加强。注意到实验表明古诺调节价曲线呈跳跃状，这意味着可能存在一系列负荷临界值(而不是一个)，在这些临界点，发电商的市场分力的组合按突变方式释放其能量，并且强度越来越大。特别当负荷达到5倍单厂总供给时，寡头发电商不仅具有加大市场分力强度的条件，也会达成某种程度上的策略默契，使市场分力的方向更为一致，市场力表现更为强劲，从而导致价格大幅上升乃至趋向无穷。这时市场力至少对价格产生两种不可忽视的影响，其一：价格调整期延长，波动幅度大，其高价位远高于均衡价格(假定均衡价格存在)；其二：均衡价格很高，或均衡价格不存在；在均衡价格不存在的情形下，价格的极限或趋于无穷，或呈现出波动幅度很大的振荡周期态。显然，这两种情形对电力市场稳定性均构成了极大威胁。

本文通过复杂自动机网络建模方法，从更广的视野俯视电力市场实验模型，通过案例实验进行分析，着重于观察与研究系统的宏观特性。虽然本文的模型仅针对单边开放的电力市场而建立，但从方法论的角度来看，完全可以推广到一般情形，对电力市场有着实际的指导作用。

[1] 薛禹胜，徐群，辛耀中，等(Xue Yusheng，Xu Qun，Xin Yaozhong，etal).加州电力危机的动态仿真和防御对策分析(一)模型的建立和定性分析(Dynamic simulation and countermeasure analyses of California power crisis Part one models and qualitative analyses)[J].电力系统自动化(Automation of Electric Power Systems)，2004，28(7):24-29.

[2] 薛禹胜(Xue Yusheng)．电力市场稳定性与电力系统稳定性的相互影响(Interactions between power market stability and power system stability)[J].电力系统自动化 (Automation of Electric Power Systems)，2002，26(21):1-6,33.

[3] 游义刚，周晓阳(You Yigang, Zhou Xiaoyang)．电力市场的信息范式(Information-theoretic approach of electricity market)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2007，19(6): 88-92.

[4] Gerard W. Complex Systems Dynamics: An Introduction Automata Networks[M].Massachusetts : Anddison-Wesley, 1991.

[5] Rudukevich A. Supply Function Equilibrium in Supply Markets:Learning All the Way[R].Cambridge, USA: Tabors Caramanis and Associates , 1999.

[6] Fudenberg D, Levine D K. The Theory of Learning in Games[M].Canbridge: MIT Press , 1998.

[7] Bower J, Bunn D. A Model-Based Comparison of Pool and Bilateral Market Mechanism for Electricity Trading[R].London: London Business School,1999.

[8] Song Yiqun，Ni Yixin， Wen Fushuan,etal.Conjectural variation based bidding strategy in spot markets：Fundamentals and comparison with classical game theoretical bidding strategies[J].Electric Power Systems Research，2003，67(1)：45-51.

[9] Ramos A， Ventosa M, Rivier M. Modeling competition in electricity energy markets by equilibrium constraints[J].Utilities Policy，1999，7(4)：233-242.

[10]Baldick R, Grant R, Kahn E. Theory and application of linear supply function equilibrium in electricity markets[J].Journal of Regulatory Economics,2004,25(2):143-167.

CournotAdjustmentAnalysisofEvolutionaryElectricityMarkets

YOU Yi-gang1， ZHOU Xiao-yang2

(1.School of Hydopower and Information Engineering, Huazhong University of Science and Technology, Wuhan 430074, China; 2.School of Mathematics and Statistics, Huanzhong Univesity of Science and Technology, Wuhan 430074, China)

This paper investigates the stability of electricity markets based on the automata network modeling method of the complex adaptation system. Firstly, the general framework of the automata network model for the experimental electricity markets is built, the generation companies and ISO comprise the bottom units, and the most basic evolutionary mechanisms are generation companies' bidding strategies and ISO's pricing methods. Then the game analyzing of the optimal pricing model is studied, the modified optimal pricing model is proposed and the gradual Cournot adjustment mode is designed. Furthermore, a typical case is selected to observe the Cournot adjustment process, and some characteristics are reasoned that there may be a series of critical loads which stimulate the generation companies release much more market power so that the Cournot adjustment prices leap up at the critical load points. The possible reason of lost stability for the electricity markets is revealed by tracing the evolutionary process of the typical cases.

electricity market； automata network modeling； evolutionary game； Cournot adjustment； market power

2009-05-20

2009-10-15

TM7

A

1003-8930(2011)01-0127-05

游义刚(1977-)，男，博士研究生，研究方向为均衡理论在电力市场中的应用。Email:cn_youyi@sina.com 周晓阳(1956-)，男，博士，教授，研究方向为复杂系统建模和分析、应用概率统计，有电力市场的演化分析，复杂自动机网络方法建模分析探索；流体计算的格子 Boltzmann 方法研究；经济和洪水数据的风险分析。Email:zhouxy_hust@sohu.com