函项分层思想及其在语言学研究中的应用

满海霞

(北京科技大学外国语学院，北京 100083)

函项分层思想及其在语言学研究中的应用

满海霞

(北京科技大学外国语学院，北京 100083)

基于现代逻辑思想的形式语义学理论，离不开类型和范畴的分层思想。它的理论源泉之一是逻辑学家弗雷格区分“完全”、“不完全”表达式的讨论，其影响主要为两方面:逻辑类型论和范畴理论。通过对比分析逻辑类型论和范畴理论在语言学领域的两个综合应用模式:蒙太格语法和类型逻辑语法可知，形式语义学总体来讲具有两种发展趋势，即偏向自然语言与偏向逻辑两种风格。

函项分层;逻辑类型论;范畴理论;蒙太格语法;类型逻辑语法

一、背景介绍

现代逻辑之父弗雷格发现，用自然语言表达逻辑概念，很难达到期望的精准程度。于是从《概念文字》(Begriffsschrifi)开始尝试提供一套检验系列推理有效性的可靠工具，并在《算术基础》(Grundgesetze der Arithmetik)中，试图将数学构造为逻辑的分支。在此过程中，弗雷格为函项给出具有一般性的定义。其区分完全(complete)和不完全(incomplete)表达式的做法，对形式语义学的发展有两方面重要的影响:

(1)弗雷格区分完全、不完全表达式的思想以及胡塞尔(Husserl)将思维对象分为若干层的想法在哲学界诱发了化学反应。列斯尼维斯基和爱裘凯维茨(Ajdukiewicz)将范畴分层思想形式化，发展出以判断语词句法行为为目的的范畴理论。在几代逻辑学家和语言学家的努力下，范畴语法逐步发展出当今形式语义学的一个重要分支——类型逻辑语法。

(2)1901年，罗素指出《算术基础》存在悖论(即著名的罗素悖论)，核心问题是，谓词是否可以做其自身的谓词?不管答案为是为否，都存在矛盾。①罗素悖论具体地说，是一个谓词是否可以做其自身的谓词?假设函项f(x)是所有不具备可做其自身谓词的元素的集合A，A={x|﹁x(x)}。那么，若承认谓词f可以做其自身的谓词，则将f作用在f上，根据集合A的定义，f(f)的值就是﹁f(f)，矛盾;若不承认谓词f可以做其自身的谓词，则f具有性质﹁f(f)，是集合A中的一个元素，根据定义，有f(f)为前提，亦矛盾。这个悖论的症结在于系统允许函项自指(self－reference)。罗素和怀特海(Whitehead)在《数学原理》中提出一种解决方案，主要思想是:通过构造基于类型的层级，为每种数学对象都配以相应的类型，具有给定类型的对象只能从更高一级类型的对象构造来，避免了函项自指造成的恶性循环。这是逻辑类型论的雏形［1］15。而后，凭借类型概念在 λ－演算(typed lambda calculus)中的重要地位，受到形式语言学家的关注，成为计算自然语言形式语义的经典依据。

范畴理论与逻辑类型论之间具有微妙而密切的联系，在现代形式语义学的研究中缺一不可。以下首先简要介绍两种理论的基础——范畴与类型之间的对应，给出两种理论之间的对应基础，然后对比二者在语言学研究中的两个综合应用模型——蒙太格语法和类型逻辑语法，说明两种应用分别代表了形式语义学偏向自然语言和偏向逻辑的两种研究风格

二、范畴与类型的对应

范畴语法所谓的“范畴”，就是将自然语言中的表达式按照句法行为特征分成若干大类，将每个大类共有的特征抽象出来，即为范畴。以最早的范畴演算系统兰贝克演算L为例［2］，L的句法系统包括两个基本范畴:np和s，分别为代表名称的范畴和代表语句的范畴。①兰贝克演算L本身使用的是n，本文为与目前主要的范畴使用标记保持一致，统一使用np。复合范畴按照定义1递归得到。

定义1 范畴形成定义

(i)np和s是范畴;

(ii)如果A和B是范畴，则A/B，BA，A·B也是范畴;

(iii)除了由(i)和(ii)生成的范畴之外，其他的都不是范畴。

其中，右斜线算子“/”、左斜线算子“”和积算子“·”为作用在相邻范畴上的范畴构造算子。积算子表示相邻范畴的直接毗连。斜线算子的情况稍微复杂，其倾斜方向表示需要结合论元范畴的方向，斜线下方和上方分别表示需要结合的论元范畴和所得的值范畴。

类型论的基本想法类似。为避免悖论，罗素将模型论中的对象置于不同的层级上，这种区分反映在类型论语言中，就是分属不同类型的表达式。假设存在一个有穷的初始语义类型集，语义类型集依据定义2递归得到。

定义2 语义类型的形成定义

令BTYPE为初始语义类型的有穷集合。TYPE是包含语义类型的最小集合，使得:

(i)BTYPE⊆TYPE;

(ii)如果 a，b∈TYPE，那么〈a，b〉∈TYPE［3］11。

类型为〈a，b〉的表达式与类型为a的表达式严格遵守函项贴合原则做贴合运算，得到类型为b的表达式。

从范畴和类型的语义定义中我们也可以看出二者的相似与对应关系。

如果将范畴“A/B”设为函项f1，把〈a，b〉设为一个函项f2，则有:

①复合范畴运算规则A/B+B→A对应函项表达式:f1(B)=A

②复合类型〈a，b〉与b的贴合运算对应函项表达式:f2(a)=b

从函项的角度看，复合范畴/类型总是比它的组成范畴/类型高一阶。换言之，函项分层思想已经编码在范畴/类型的定义中。f1和f2相似，但不相等。主要原因在于，范畴的斜线构造算子区分方向，f1不但可以对应“A/B”，同时也可做复合范畴“BA”的对应函项;而类型不需要区分论元的结合方向，所以f2相当于f1不区分方向的版本。这体现了句法范畴与语义类型之间具有一定的对应关系(定义3)，也从宏观上保证了范畴理论与逻辑类型论的对应，保证形式语义学句法和语义两方面理论的同步发展。

定义3 范畴到类型的对应

令τ是一个从范畴集到类型集的函项。τ是对应函项，当且仅当

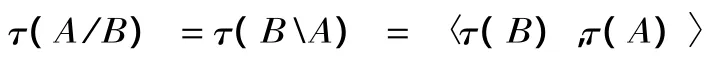
定义3说明，给定一个范畴，就可以从这个范畴的内部结构预测出它所对应的语义类型。从逻辑的角度看，即一个语言符号串的语义类型是其句法范畴的同态像(homomorphic image)。换个角度考虑，类型和范畴只不过是函项分层思想对自然语言语词在语义和句法上的两种标记。不过，句法范畴到语义类型的对应关系不是一对一，而是多对一。以蒙太格语法(Montague Grammar)为例，其初始类型有两个:e(entity)和t(truth)，语义上分别对应个体和真值，通常情况下，分别被映射到个体集合E和真值集合{0，1}上［4］。以语句“John walks”为例，在语义上看，“walks”是所有具有走路性质的个体组成的集合，如定义4所给“walk”在模型M1中的语义定义。这里单词的全小写字母表示它在模型论域中对应的个体，单词大写表明它所对应的逻辑式，〖〗表示自然语言表达式在模型中对应的语义值。

定义4 “walk”在M1模型内的语义定义

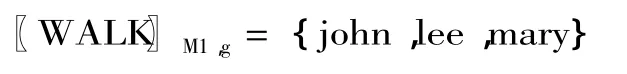
从图1可以看到，“walk”的语义值是将e类型个体映射到t类型真值的集合上的函数，即fWALK(e)=t。因此，WALK对应类型，〈e，t〉。②此处为简化问题，不讨论专名的类型提升。只强调一点，在蒙太格语法中，为保证专名与量词能够做一致处理，专名的类型被提升为〈〈e，t〉，t〉，而非e。没有类型为e的自然语言表达式，类型为e的只是模型论中的个体。详细讨论参见参考文献［5］。如果已知它的句法范畴，依据定义3，从它到语义类型的映射结果是唯一的，为〈e，t〉。反过来，如果已知“walks”的语义类型，往回推溯则只能推断“walks”句法范畴的2种可能情况:nps或者s/np。

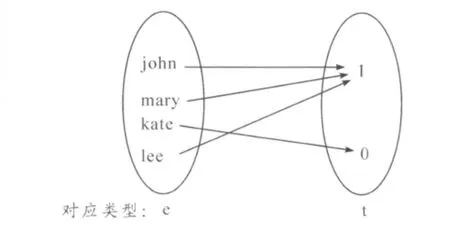
图1 〚WALK〛M1，g的特征函项直观图

需要说明的是，在对语言学的应用中，执行语义运算工作的是基于类型的λ－演算，参与运算的基本单位是自然语言符号串在λ－演算中的翻译，即语义表达式。虽然参与运算的不是类型本身，但是语义表达式的运算基础是他们对应的类型，要求类型之间能够依据λ－演算做应用或者抽象运算。基本想法如定义5。

定义5 λ－演算的两条运算规则［6］

对于每个类型，都允许(i)和(ii)中λ－项的构造:

(i)如果t1的类型为〈a，b〉，t2类型为a，则t1(t2)是类型为b的项;(λ－应用)

(ii)如果t的类型为b，x是类型为a的变元，则(λx.t)的类型为〈a，b〉。(λ－抽象)

三、语言学应用:蒙太格语法与类型逻辑语法

总之，从宏观上看，正是逻辑类型论与范畴理论之间的相似和对应，使蒙太格给自然语言的句法找到遵循组合原则的语义解释，开创了用形式方法研究自然语言语义的先河;也正是这种相似和对应，使范·本瑟姆(van Benthem)为范畴语法配备了基于类型的语义解释，从而推进了范畴语法的当代形式——类型逻辑语法的产生和发展。

20世纪60年代末70年代初，美国杰出数理语言学家蒙太格以其特有的逻辑高度，发现范畴语法在结构上同表现自然语言语义的逻辑类型论间有着惊人的相似，并看到自然语言与形式语言在本质上是相同的。因此，蒙太格尝试以类型为基础，依据组合原则构建一套通用的语法(Universal Grammar)，来描述逻辑人工语言和自然语言间的某些共同规律，由此开始了用形式方法研究自然语言语义的思路［7］32。80年代初，范·本瑟姆［8］受蒙太格语法的启发，为范畴语法配上了语义系统(即Lvb演算)，弥补了范畴语法在语义组合方面的欠缺，孕育出范畴语法的一个当代形式—类型逻辑语法。几个理论之间的关系可用图2表示。

图2中的箭头表示“启发”与“促进”，其中蒙太格语法和范畴语法之间的关系很有意思，大有互相帮助、共同进步的意味。一方面，范畴语法是蒙太格语法的理论基础之一，另一方面，蒙太格语法在语义构造上的独特视角又启发了范畴语法语义系统的产生，间接促进了范畴语法后继理论——类型逻辑语法的出现。

(一)蒙太格语法

蒙太格语法的具体做法是:首先，确立句法范畴和语义类型之间的对应关系。其描述自然语言句法生成的句法规则以范畴语法为基础，依据规则对规则假设，令一条句法规则有一条语义规则相对应，语义规则的基本单位λ－项之间以λ－演算为基础，从而使得用形式化方法研究自然语言语义成为可能。在蒙太格语法中，句法和语义运算展示的是类似自然语言句法和高阶谓词函项的操作。以蒙太格构造的英语部分语句系统PTQ为例，一共包含17条句法规则和对应配备的17条语义规则。比如从及物动词生成不及物动词的句法规则S7:

S7:如果δ∈PTV，且α∈PT，则F6(δ，α)∈PIV，且F6(δ，α)=δα'。其中，如果α是句法变元，则α'是α的宾格形式，否则α'=α。［8］166

S7中，δ、α为自然语言符号串，PA指示由所有范畴为A的语言符号串组成的集合，下标IV、TV分别代表不及物动词和及物动词的范畴，T为函项范畴S/IV，F6是对自然语言符号串做句法操作的函项。从S7可以看出，蒙太格语法中的词表是按范畴分类的若干集合，如:PTV={love，like，play}，PT={Mary，John}。那么，依据S7，“love Mary”的句法生成过程就是:

δ=love∈PTV，α=Mary∈ PT，love和Mary毗连之后属于范畴为IV的语言符号串集合，二者的毗连结果F6(love，Mary)=loveMary。如果把Mary换成句法变元he，那么依据F6，运算的结果就是lovehim，因为根据S7的最后一句注解规定，要把he换成其宾格形式。

可以看出，蒙太格语法中句法系统类似自然语言语法。它将自然语言按照范畴分为不同的大类，抽象出具有相同或不同范畴的语言符号串之间进行毗连的规律，制定成系统的句法规则。这个句法系统是一个开系统，可以根据所选自然语言语句系统的句法要求增加规则，如邹崇理构造的处理汉语时态结构的部分语句系统，就包含21条句法规则［9］400－422。

同时，在语义方面，蒙太格给自然语言表达式指派相应的逻辑式，这个逻辑式是以类型为语义载体的，或者说，是以图2中提到的“基于类型的λ－演算”的运算单位—λ－项为语义载体。然后，要对应相应的句法规则，制定从自然语言表达式到逻辑表达式的翻译。以S7对应的翻译规则T7(如下)为例(其中α|→β意味:自然语言表达式α被翻译成逻辑式β):

T7:如果δ∈PTV，α∈PT，且α|→α'，β|→β'，则F6(δ，α)|→ δ'(α')。［8］167

因此短语“love Mary”的语义组合过程为:love |→λxλyLOVE'(x)(y)，Mary|→MARY'，所以love和Mary进行句法毗连之后，语义上的组合结果是λyLOVE'(MARY')(y)(定义5中的λ－应用规则)。这里，在运算过程中看到的，都是从自然语言语词出发进行的形式计算，相比之下，另一种语言学应用—类型逻辑语法—则显得更加抽象，逻辑味道更加浓重。

(二)类型逻辑语法

基本的类型逻辑语法也包括句法系统和语义系统，前者是兰贝克演算L，后者则是定义5提到的λ－演算。不严格地说，对于类型逻辑语法，兰贝克演算说明了什么结构是可能的，λ－项则描述了这些结构如何进行运算。

在类型逻辑语法的词库中，每个词条都对应一个序对，它包含两方面信息，一是它所对应的句法范畴，一是代表其语义的λ－项。仍以“John walks”为例，它们在词库中对应的词条分别为: John:〈np，JOHN'〉;walks:〈nps，WALK'〉，该句在类型逻辑语法中的生成过程如图3所示。

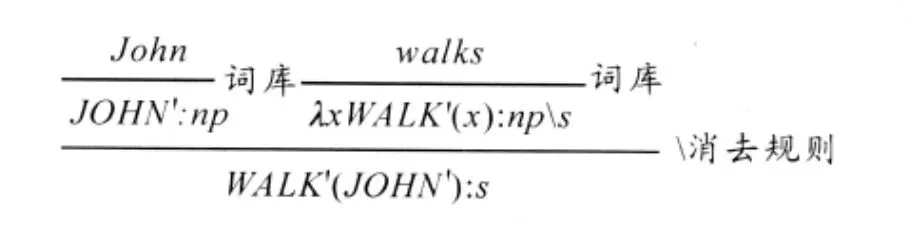
图3 “John walks”的类型逻辑生成图①图3的类型逻辑生成并不严格。在类型逻辑生成过程中，一般来说，语词的逻辑式都经过范式化，计算中使用的都是最简的形式。如这里面“walk”的逻辑式还可以再做η－划归，变成“WALK'”。

如果不做深层次考虑，单看词条之间的运算关系，至少能得到这样的可行性信息:每个范畴对应一个语义类型，而λ－运算是基于类型的，这为类型逻辑语法提供了一个很好的句法 －语义接口，保证句法运算和语义组合有实现并行推演的基础。

四、形式语义学的两个发展方向

形式语义学又称逻辑语义学，顾名思义，是关于逻辑学和语言学交叉领域的研究。事实上，蒙太格语法与类型逻辑语法之间的差异和特色恰好反映了形式语义学研究的两大方向。蒙太格语法属于语言学意味较浓的形式语义研究，类型逻辑语法属于突出对自然语言做形式分析的逻辑风格研究。

对比考察表1可以看出:(1)在范畴的应用上，类型逻辑语法将自然语言的毗连规则抽象为范畴间的贴合规则，以范畴为基本单位参与句法运算;而对于蒙太格语法来说，范畴表面上的功能只不过是自然语言表达式分类的标准和标签，参与句法运算的，是属于这一范畴集合的自然语言表达式。蒙太格改变了强调范畴运算甚于语言生成的做法，把范畴的运算置于幕后的次要地位。(2)在对自然语言词条的使用上，蒙太格语法不管是对句法规则还是语义规则，都是从自然语言词条开始，或做句法毗连，或赋以语义翻译;而在类型逻辑语法中，这些工作都转给了词库，从词库出来便不见自然语言表达式的踪影，运算过程中看到的都是句法范畴和语义λ－项。

从表1中“词库”一横栏开始对比两种语法，可以得出以下结论:类型逻辑语法几乎总是更加抽象一层;反过来，蒙太格语法总要更贴近自然语言一些，在其中看到的自然语言表达式的影子要多些。以句法系统为例，二者的句法系统都由一系列句法规则构成，但是蒙太格语法的句法规则表现的是对自然语言表达式之间如何结合的规定，说明它们之间是什么贴合顺序、句法上有什么转化等，句法规则的增加与语句系统中语词之间的毗连情况有关。至于类型逻辑语法，它的句法系统则是一个逻辑系统，表现的是抽象的范畴之间的毗连规律，每增加一条规则或者联接词，都要经过严格的证明和推导。

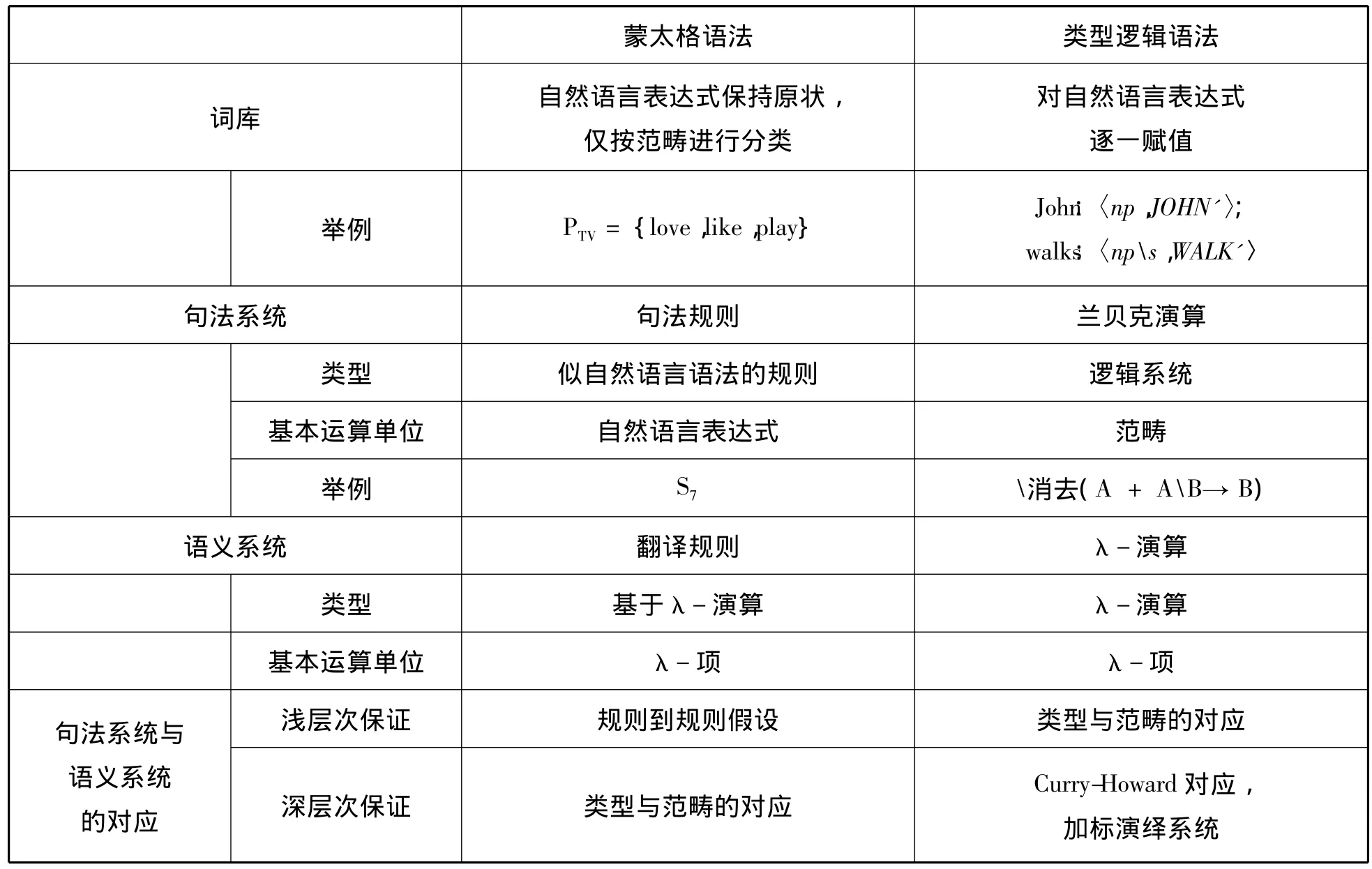
表1 蒙太格语法与类型逻辑语法基本机制对比

见微知著，从函项分层理论在语言学领域的两个应用，可以看出形式语义学的主体发展趋势:偏向自然语言与偏向逻辑两种风格。前者以蒙太格语法为代表，其分析更接近自然语言，抽象程度不高;后者以类型逻辑语法为代表，其分析更接近逻辑的风格，对形式化的构造也要求有更高的抽象度和精准度。两种力量之间相互影响、互相促进，如图2所示。但是，无论蒙太格语法还是类型逻辑语法，都是函项分层思想的两个后继理论——类型论和范畴语法在语言学领域的综合应用模式，是语言学与逻辑学交叉领域研究的缩影。目前，类型论和范畴理论已成为计算机领域重要的基础理论［10］，并在计算科学界取得了广泛的应用［11－12］。从对二者的综合分析与对比，我们可以看出，逻辑类型和句法范畴的结合将为形式语义学的发展提供更多的研究成果、更广阔的研究空间，也将为自然语言程序化提供更成熟更有指导意义的元理论思想和依据。

［1］Kamareddine，Fairouz，Laan Twan，Nederpelt Rob.A Modern Perspective on Type Theory:From its origins until today［M］.New York，Boston，Dordrecht，London，Mos－cow:Kluwer Academic Publishers，2005.

［2］Lambek Joachim.The Mathematics of Sentence Structure［J］.The American Mathematical Monthly，1958(3):154－170.

［3］Jäger Gerhard.Anaphora and Type Logical Grammar［M］.Dordrecht:Springer，2005.

［4］Montague，Richard.Formal Philosophy［M］.New Haven: Yale University Press，1974.

［5］满海霞.形式语义学两题［J］.毕节学院学报，2010 (2):37－41.

［6］van Benthem，Johan.The semantics of variety in categorial grammar［C］//Categorial Grammar.Amsterdam:Benjamin，1988.

［7］邹崇理.范畴类型逻辑［M］.北京:中国社会科学出版社，2008.

［8］GAMUT L T F.Logic，Language and Meaning(II)—Intentional Logic and Logical Grammar［M］.Chicago and London:The University of Chicago Press，1991.

［9］邹崇理.自然语言逻辑研究［M］.北京:北京大学出版社，2000.

［10］Asperti Andrea，Longo Giuseppe.Categories，Types and Structures:An Introduction to Category Theory for the Working Computer Scientist(Foundations of Computing Series)［M］.Cambridge:The MIT press，1991.

［11］高东平.申请专利:一种基于类型论的汉语分词方法［S］.专利申请号:200910078879.0，2009.

［12］Moot，Richard.Proof Nets for Linguistic Analysis［D］.Dutch:Utrecht University，2002.

Function Stratification and Its Application in Linguisitics

MAN Hai－xia
(Foreign Language Department，University of Science＆Technology Beijing，Beijing 10083，China)

Formal Semantics，originated from Modern Logics，is inseparable from the concept of function stratification.One of its theoretical sources is the classification over complete and incomplete expressions by Frege，the influences of which mainly reflected in two aspects:Type theory and Categorial Grammars.In addition，the present paper compares two integrated models that Type theory and Categorial grammars applied to—Montague Grammar and Type Logical Grammar，in order to demonstrate two major trends during the development of Formal Semantics，namely，pro－Linguistics and pro－Logics.

Function stratification;Type theory;Categorial grammars;Montague Grammar;Type Logical Grammar

B81

A

1674－8425(2011)08－0083－06

2011－06－30

国家社会科学基金项目“面向自然语言信息处理的范畴类型逻辑研究”(09BZX046)。

满海霞(1983—)，女，内蒙古自治区乌兰浩特人，博士，讲师，研究方向:形式语义学、语言逻辑。

(责任编辑 邝坦励)