实验法建模在过程控制教学中的应用浅谈
马彦霞 王燕 张谦
中原工学院 郑州 450007
实验法建模在过程控制教学中的应用浅谈
马彦霞 王燕 张谦
中原工学院 郑州 450007
对象的数学模型是分析和设计过程控制系统的基础资料。主要以单水槽为例,讨论在过程控制课程中采用的实验法建模的一般过程及其数据处理方法,并根据实际经验指出此方法在应用过程中应该注意的问题。
过程控制;实验法;建模
Author’s addressZhongyuan University of Technology, Zhengzhou, China 450007
1 引言
过程控制是自动化和测控等相关专业一门重要的专业课程,主要涉及过程控制系统的分析和设计方法。对象的模型是设计和分析控制系统的基础和关键资料,在过程控制课程中讨论的建模方法主要有机理法和实验法两种[1-2]。机理分析法具有较大的普遍性,需要有足够的经验,要充分了解过程的内在机理。实验法建模跟机理法相比,不需要深入了解过程复杂的内在机理,同时还可以直接获取模型的参数。因此,实验法和机理法往往相互配合在过程控制系统建模中得到广泛应用[3-4]。本文结合实例,通过图文分析将实验法建模的过程和应用展示给学生,既提高学生的兴趣,又取得良好的教学效果。
2 实验法建模
实验法建模是在实际的生产过程中,根据过程的输入、输出实验数据来获得过程的数学模型,工程上通常采用加阶跃输入信号的方法。
2.1 由阶跃响应曲线形状选定模型结构

图1 水槽装置图
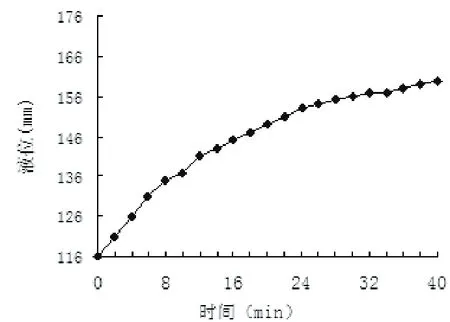
图2 液位阶跃响应曲线
绝大部分工业过程的动态特性具有自衡能力,因此其模型可以近似地以一阶、二阶、一阶加滞后、二阶加滞后特性之一来描述。需要建立模型的对象如图1所示。
实验中,在保持水槽液位稳定在116 mm初始值的基础上(这一点很重要,首先保持对象参数的稳定,避免其他信号的干扰),再由控制器输入阶跃扰动量:x0=1.6 mA。测得的阶跃响应实验数据和阶跃响应曲线分别如表1和图2所示。从图2中可以看出,实验中得到的曲线其形状和一阶惯性环节的理论曲线形状相似,在t=0时刻曲线的斜率最大;随着时间的推移,曲线的响应越来越缓慢直到最后稳定下来。因此,把对象的模型结构近似为一阶惯性环节:
2.2 确定模型结构参数K、T
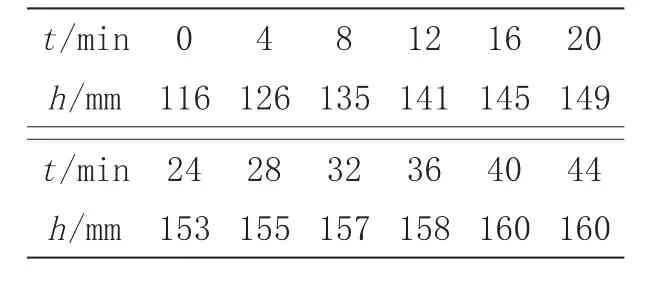
表1 水槽液位阶跃响应数据
1)作图法。在阶跃响应曲线t=0处做曲线的切线,该切线交y(∞)于A,OA在时间轴上的投影OB就是时间常数T。从图3中可以读出T≈17 min。
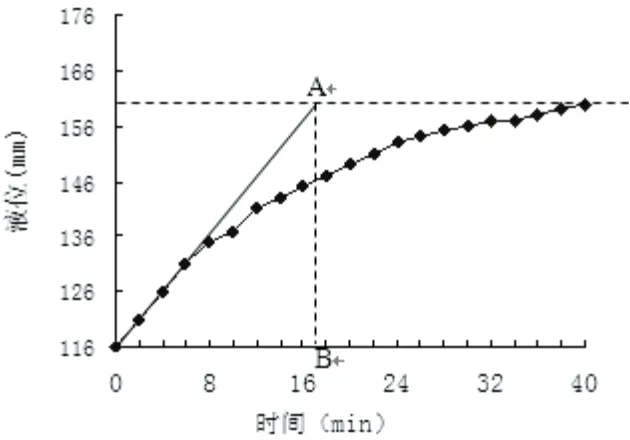
图3 作图法
2)计算法。在初值为0的条件下,一节环节的液位与时间的时域表达式为因此,从图2中任意找到一个点,将坐标值代入上式即可得到一个T值。为了应用方便,在计算法中通常先将阶跃响应曲线值y(t)减去初值y(0),然后除以y(∞)值,得到y*(t)值,即:
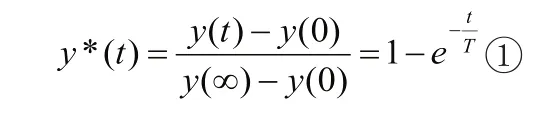

图4 计算法
从而得到一个新的所谓的标准阶跃响应曲线y*(t)(从0到1变化),如图4所示。在标准曲线上得到两个
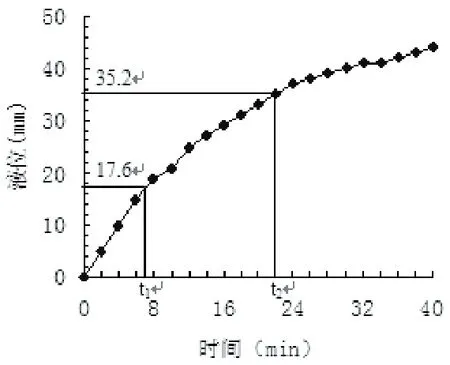
图5 两点法
点:y*(t1)=0.632,y*(t2)=0.33。按式①计算得:

据式②和③,取T=(T1+T2)/2=14.5 min作为时间常数T值。
3)两点法。如图5所示,两点法求参数T是在初值为0(即y(t)-y(0))的液位坐标上选取2个特殊的点:y(t1)=0.4,y(∞)=17.6所对应的时间t1;y(t2)=0.8,y(∞)=35.2所对应的时间t2。得到t1/t2=7/22≈0.32,所以时间常数T=(t1+t2)/2.12≈14 min。
3 结论
通过以上3种方法求取T的值分别为17 min、14.5 min和14 min。其中计算法和两点法的结果比较接近,水槽对t象的模型参数可以表示为mm/mA。可以看出,作图法最简单,但是由于学生在做切线时方向不易确定,可能会造成较大的误差,因此这种方法可用于对模型要求不高的场合;计算法相对比较精确,使用此方法时一定要将所有的实验数据值减去初始值获得初值为0的条件(这是学生在应用时最容易忽略的一步,而是直接利用初始的阶跃响应数据),同时要将阶跃响应曲线转换为标准曲线y*(t)才能应用;两点法虽然不需要获取标准的阶跃响应曲线,但也要满足初值为0的条件,而且此方法不适用于含纯滞后环节的过程。同时,在应用上述方法进行实验法建模时,还要强调学生注意在相同的条件下重复测量几次,将两组以上比较接近的实验曲线作为模型处理的依据,并注意3种处理方法适用的场合。
[1]邵裕森,戴先中.过程控制工程[M].北京:机械工业出版社,2003
[2]孙洪程,李大字,翁维勤.过程控制工程[M].北京:高等教育出版社,2006
[3]张中明,吴晓苏.基于实验法的焦炉集气管压力数学建模及其自动调节的实现[J].工程设计学报,2009,16(3):217-222
[4]姜洪源,Ulanov A M.实验建模方法在金属橡胶隔振系统分析中的应用[J].实验力学,2002,17(3):363-368
Application of Modeling based on Experimentation in Process Control
//Ma Yanxia, Wang Yan,Zhang Qian
The mathematical model of a controlled subject is basic and important for analyzing and designing process control systems. In this paper, the modeling process of a single tank based on experimentation and its data processing method is discussed respectively. And the notable problems of the method during modeling are proposed, too.
process control; experimentation; modeling
TP271,TP272
B
1671-489X(2011)12-0109-02
10.3969/j.issn.1671-489X.2011.12.109
作者:马彦霞,讲师,主要从事电气工程及其自动化方向的教学和研究工作。

