浅谈比较法在概率论教学中的作用

石莲英

（闽南理工学院，福建 石狮 362700）

浅谈比较法在概率论教学中的作用

石莲英

（闽南理工学院，福建 石狮 362700）

比较法是一种常用的数学思维方法，它能使学生在识同辨异的过程，加深对概念和定理的理解，还有助于发现问题，活跃思维，达到对事物的本质的认识。在概率论教学中，恰当的运用比较法教学，可以帮助学生加深对该课程的理解，并激发他们思考的积极性，从而提高教学质量。

比较法；概率论；作用

著名教育家乌申斯基认为：“比较是一切理解和思维的基础，我们正是通过比较来了解世界上的一切的。”概率论是研究随机现象统计规律的一门数学学科，其中的大量知识点之间既有联系又有区别。因此，在概率论的教学中比较法的使用是必不可少的。恰当的使用比较法，不仅能突出教学重点，突破教学难点，而且还能加深对事物的本质的认识。在传统的概率论教学工作中，主要是以陈述或证明为主，但实际上，运用比较法对概率论的教学有着重要的作用，它不仅可以纠正学生的错觉，还可以使学生在识同辨异的过程，加深对正确概念和定理的理解，并能激发学生学习的积极性。

1.利用比较法加深对概念和定理的理解

由于概率论本身含有大量抽象的概念和定理，而这些概念和定理之间即有联系又有区别，能否准确地理解和把握这些概念和定理的内涵，掌握概念和定理的本质属性，是能否正确掌握概率论知识的关键所在。若我们在使用实例对这些概念进行阐述的同时，能恰当的使用比较法，则可从另一方面抓住概念的本质，从而加深学生对这些概念和定理的理解。

例如，在随机事件的诸多事件的关系中，有两个在计算中常见的，也是学生比较容易混淆的，就是事件的互斥及互逆关系.为了加深学生对这两个事件关系的概念的理解，现做比较如下：

（1）概念的比较：

互斥事件是两个不可能同时发生的事件；互逆事件是两个不可能同时发生而两者又必发生其一的事件。若用符号来表示：已知A，B两事件，若A与B互斥，则AB=φ；若A与B互逆，则有A+B=U，AB=φ（这里U表示必然事件，φ表示不可能事件）。

（2）应用的比较

①A，B互斥时，且 p( A) = 0.2,p( B) =0.5，则p( AB)=________， p( A +B)=_________。

②A，B互逆时， p( A +B)=________，

p( A) = 0.2时，p( B)=________。

答：① 0；0.7。 ②1；0.8。

注：在加深对概念的理解的前提下，我们就可简单地进行计算了，在①中，A，B互斥，即AB=φ，则有 p( A B)= 0；根据任一事件概率的加法公式：p( A + B) = p( A) + P( B) - P( A B)，而在互斥事件中， p( A B)= 0，则可得互斥事件的加法公式：p( A + B ) = p( A) + P( B)，根据互斥事件的加法公式：p( A + B ) = p( A) + P( B) = 0.2 + 0.5 = 0.7；在②中，A，B互逆，则有A+B=U，即 p( A +B)= 1；因为A，B互逆，于是可记，再根据互逆事件的性质，可得

总之，在概念的比较过程中，加深了学生对概念的理解。在熟练掌握概念的前提下，进行应用的比较，使学生从另一方面抓住了概念的本质，从而进一步加深了对概念的理解。

2.利用比较法识同辨异，揭示规律，拓广知识面

概率论的知识点之间可能有部分相同或相似，但不可能完全相同，为了区分异同点，抓住知识点的本质区别，就必须要有一个比较的过程。这一比较过程有如下两种情况：一是先给出相似的知识点，并对这些知识点进行清楚的分析，通过分析，抓住知识点各自的本质特征；二是对给出的知识点的概念及本质进行比较，抓住其本质区别，使学生对这些知识点的概念有个准确地认识，从而揭示规律，拓广知识面。如在取球事件的教学中，主要有两种取法：有放回抽样；不放回抽样。已知袋中含有的球数、颜色等均相同，但取法不同，最后的结果也是有所区别。

例 袋中有3个红球，4个白球，从中任取两次，每次取一个球，求

（1）有放回抽样，取得两个球都是白球的概率；

（2）不放回抽样，取得两个球都是白球的概率。

解 设 Ai={第i个取到白球}，第i个取到红球}（i=1,2）

注：在（1）中，因为是有放回抽样，第一次取到白球与第二次取到白球的概率互不影响，其概率都是即这两事件是相互独立的，所以有公式而在（2）中，因为是不放回抽样，则第一次是否取到白球对第二次取到白球的概率就有着直接的影响，若第一次取到白球，则第二次取到白球的概率若第一次不取到白球（即取到红球），则第二次取到白球的概率均为条件概率，根据条件概率的定义，可得乘法公式：

总之，通过比较，我们发现，虽同为取球事件，且在相同的条件下，但取法不同，其结果完全不同；通过比较，我们可得规律：在有放回抽样中，事件之间相互独立，可根据独立事件的性质进行计算；在不放回抽样中，事件之间相互影响，要根据条件概率的性质进行计算；通过比较，使学生对取球事件的两种取法，有了更深的理解，这不仅使学生同时掌握了这两种取球方法，拓宽了知识面，而且还提示学生解题过程中应注意审题，一字之差，会有完全不同的结论。

3.利用比较法发现问题，培养学生良好的思维品质

概率论的知识点之间既有联系又有区别，通过反复比较，学生不仅会发现一些有趣的问题，而且还能在不断地探索过程中，养成良好的思维品质，体会到思索的乐趣。

如在事件之间的相互独立关系的学习当中，容易得知：（1）若事件A，B相互独立，即在一次随机试验中事件A是否发生与事件B是否发生互不影响。（2）若事件A与B相互独立，且 p( A)＞ 0，p( B)＞0，则有 p( A B ) =p( A) p( B)。

在学习了事件之间的相互独立关系之后，爱思考的一些学生，就会将相互独立的事件与之前学过的互斥事件进行比较。经过比较，发现了问题：相互独立的事件是互斥事件吗？

对此，从下列三个方面进行比较：

（1）首先，要明确事件的相互独立与互斥事件是完全不同的两个概念，它们是从两个不同的角度来表述事件之间的某种关系的。互斥事件表示在一次随机试验中不可能同时发生的事件；而相互独立表示在一次随机试验中某一事件是否发生与另一事件是否发生互不影响。

（2）其次，当p( A)＞0，p( B)＞0时，若事件A，B相互独立，则A与B必不互斥。因为，事件A，B相互独立，则有p( A B ) =p( A) p( B)，又 p( A) p( B)＞ 0，即 p( A B) ＞ 0，所以A与B必不互斥。

（3）最后，还可证明：若事件A与B既相互独立，又互斥，则事件A与B中至少有一个是零概率事件（也就是不可能事件）。

通过上述比较，就轻而易举地解决了学生所提出来的问题。

除了上面提出的问题外，还可在相互独立的事件的解题过程中，对其解题方法做了进一步地思索：

例 已知甲、乙射手命中敌机的概率分别是0.8，0.9，他们各自独立地向同一敌机射击一次。试求此敌机被击中的概率。

解 设A={甲击中敌机}，B={乙击中敌机}，于是

因为“敌机被击中”即“甲、乙中至少有一人击中敌机”，故本题实际上求的是A+B的概率。根据A，B的独立性，有如下两种解题方法：

解法一 根据任一事件概率的加法公式，有

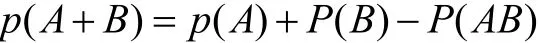
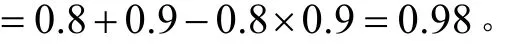
解法二 根据事件与其互逆事件的关系及事件的独立性，有

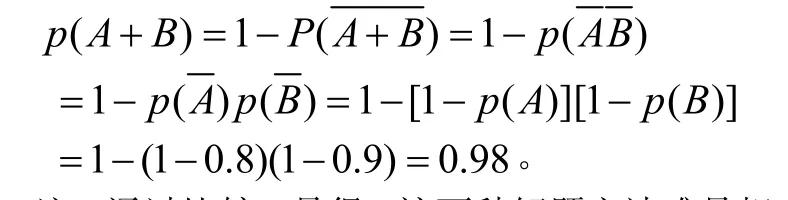
注：通过比较，易得，这两种解题方法难易相当，但若构成和事件的独立事件个数较多时则方法二更具优越性。

通过从问题的提出到解决这一过程，以及对解题方法的思索，使学生在不断地探索过程中，逐步养成良好的思维品质，从而体会到学习的乐趣。

4.利用比较法发现并纠正错误

在辨析错误时，比较法具有直观，说服力强等特点，它不仅能使学生明显的判断出错误所在，而且还能弥补相关知识，获得正确的结论。

下面以一个例题加以说明。例 袋中有3个黑球，4个白球，它们除颜色不同外，其它方面没有差别，现在随机地把球一个接一个地摸出来，求第一次摸出的球是黑球的概率，以及第二次摸出的球是黑球的概率。

解 设 Ai={第i次摸出的球是黑球} ，={第i次摸出的球是白球}(i=1,2)，于是，有

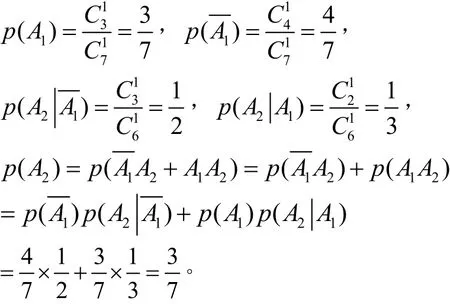
在上述随机摸球事件中，大多数学生会认为第一次摸黑球与第二次摸黑球的概率不同，而且互相影响，若第一次摸黑球，则第二次摸黑球的概率一定会比第一次摸黑球的概率小，通过比较，不仅澄清了学生的错误所在，而且还得到了正确的结论：在上述随机摸球事件中，第i次摸出的球是黑球的概率都是相等的(1≤i≤7)。

5.小结

在概率论的教学中，恰当的应用比较法，能加深对概念和定理的理解；能识同辨异，揭示规律，拓广知识面；能发现问题，培养学生良好的思维品质；而且能发现并纠正错误。总之，恰当的运用比较法教学，有助于加深学生对该课程的理解，激发其学习的积极性，从而提高其概率素养。

[1] 姚孟臣.高等数学[M].高等教育出版社，2008.

[2] 顾静相.经济数学基础[M].高等教育出版社，2008.

[3] 吴赣昌.线性代数与概率统计[M].中国人民大学出版社，2009.

Discusses about the function of comparison test in the theory of probability teaching

SHI Lian-ying

Comparison test is a commonly used mathematical way of thinking, it enables students to identify with Distinction in the process, to deepen understanding of concepts and theorems, but also helps to identify problems, active thinking, to achieve understanding of the nature of things.In the theory of probability teaching, the appropriate utilization comparison test teaching, may help the student to deepen to this curriculum understanding, and stimulate their thinking about the enthusiasm, is helpful in improves the quality of teaching.

comparison test；theory of probability； affects

G642.3

A

1008-7427（2011）12-0135-02

2011-10-18