基于分形的三维海面研究及生成

◆庄建东 曾勇进

(集美大学计算机工程学院计算机教研室)

基于分形的三维海面研究及生成

◆庄建东 曾勇进

(集美大学计算机工程学院计算机教研室)

1 引言

虚拟自然环境如地形、植物、海浪、云和火焰等的计算机模拟一直是计算机图形学的重要研究课题之一，其中海浪的模拟相比其他自然环境的模拟更为复杂和困难。当前对于海浪模拟仿真的建模方法根据具体实现原理可分为:基于计算流体力学方法、基于海浪谱方法、基于几何造型方法和基于分形几何方法。

基于计算流体力学的方法虽然能够生成逼真的海浪运动效果，但是由于其求解过程过于复杂，在实际应用中一般很少使用。基于海浪谱方法只能模拟海浪的波动效果而不能模拟海浪的翻转卷曲效果。基于几何模型方法是根据海浪的形态特点，选择几何曲线或曲面构造连续变化的海浪形状。基于分形几何方法一般采用FBM方法，生成海浪的分形曲面将生成点的坐标设定为时间和空间相关的函数，进而生成海浪效果，同时通过插值的方法保证图像的连续性有，因而在实际得到广泛应用。

本文希望通过对海浪模拟仿真的建模方法的深入研究，以便能更好地了解和掌握如何通过计算机实现模拟自然界中的自然景观技术打下基础。

2 静态海浪生成的原理及算法

分形几何学的基本思想是:客观事物具有自相似的层次结构，局部与整体在形态、功能、信息、时间、空间等方面具有统计意义上的相似性，成为自相似性。而悬浮微粒永不停息地做无规则运动的现象叫做布朗运动。分形理论最早是由美籍数学家曼德布罗特提出的，分形的重要特征之一就是自相似性，而海浪就可以看作是周期性的不同尺寸波形的叠加，这些不同尺寸的波形具有大尺度相关而小尺度相似的特征，且空间各向近似同性，即海浪具有自相似的特征，由这种自相似性可看出海浪具有分形特征。基于这个特征，可以利用少量数据生成具有较强真实感和实时性的海浪波动效果。

分形布朗运动(Fractional Brownian Motion)是由 B.Mandelbrot和、V.Ness于1968年针对随机布朗运动的推广，提出的一种统计自相似过程的数学模型，主要用于生成布朗运动过程。

中点位移又叫做随机中点位移法，是最简单和经典的方法，是对分形布朗运动的直接应用。一维随机中点位移法的思想史:针对某一已知端点高程(或属性)的线段，其线段中点的高程(或属性)为其两端点高程(或属性)的平均值再加一随机位移量，位移后的两线段再进行上述中点细分并位移，递归直到满足所需的分辨率为止。将其推广到二维，依据表面构网方式的不同，其模拟可分为三角形边线细分法、方形－方形细分法、菱形－方形法等方法，其实现思想与一维类似。本文采用的是菱形－方形法。

2.1 菱形－方形法

海浪分形曲面的生成使用FBM插值方法中的随机中点位移算法.随机中点位移算法一般包括三角形边界法、方形法、菱形法、菱形－方形法等，下面介绍本文所采用的菱形－方形法.

如图1所示，首先从一个正方形的4个角点开始，这4个角点A、B、C、D分别具有不同的高度值hA、hB、hC、hD值，然后计算出中点O的高度值hO，再根据4个角点的位置计算出四边形各边中点位置，同时计算出各边中点的高度值:

这样在第一次细分过程中可以由一个正方形生成4个正方形，如图1所示。其中●为初始正方形角点，○为根据4个初始正方形角点生成的初始正方形中点，■为根据4个初始角点和生成的正方形中点计算出的正方形4边中点，这样就生成了4个新的正方形，同时计算各个点的高度值。以此类推，第二次细分可生成16个正方形，第三次则可生成64个，经过i次细分生成的正方形为2(2i)个。

由于生成各点高度不同，经多次迭代后可生成一个近似曲面，这个曲面与真实海浪形状比较接近，但是由于PC机硬件性能所限，迭代次数不能过多，以避免大量运算可能产生的计算错误。

图1 菱形－方形细分法

2.2 基于分形的三维静态海浪建模及实现算法

2.2.1 分形海面绘制算法

为了实现海浪运动效果，首先需要画出静态海浪曲面，没分形前是1个正方形，第一次分形产生4个正方形，第二次细分可生成16个正方形，第三次则可生成64个，经过i次细分生成的正方形为22i个。

同样由于PC机硬件性能所限，迭代次数不能过多，以避免大量运算可能产生的计算错误，本课题最多只采用8次迭代。如图所示经过8次分形迭代所生成的静态海浪曲面效果图。

图2 八次分形迭代的静态海浪曲面效果图

基于FBM方法的曲面生成算法如下:

(1)确定迭代初始正方形个数g及迭代次数n。

(2)确定随机函数方程g()=(rand()%(r－1)－r/d)。

(3)初始迭代次数m=0，然后对初始正方形的4个角点分别赋予随机高度值hA、hB、hC、hD，并将生成的坐标保存到坐标数组中。

(4)令当前迭代次数m=m+1，计算当次迭代所生成的所有点的坐标值，并保存到坐标数组中。(5)重复第4步，直到当m=n－1时为最后一次迭代过程，结束迭代。(6)使用纹理映射方法将海浪源纹理映射到生成的曲面上，生成海浪分形图形。

3 运动海浪的生成的原理及算法

海浪的运动特征很复杂，主要表现为形状不规则，具有复杂性和随机性。海浪的运动特征，可以概括为近似周期性的规则波形的叠加，即海浪的运动形态可以看作是由一系列具有不同频率、波数、波高和传播方向的规则波叠加而成，类似于简单三维进行波，根据海浪的这种运动特征可以使用多个正弦或余弦波叠加来近似地表示海浪的运动形态。

3.1 海浪运动的几何模型

基于分形方法生成的海面是静态的，为了实现海浪运动的效果，需将构成海面点的高度值设为随时间和空间变化的函数，而海浪的运动形态可以看作是由一系列具有不同频率、波数、波高和传播方向的规则波叠加而成，类似于简单三维进行波，它的单一波形分量形式为:

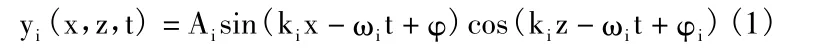
也就是说，在t时刻的波面可以看成是具有不同波高和不同频率的n个波的总和。下面介绍各个参数的确定方法。

表1 风级、波浪高度和波动周期的仿真参数

3.2 海浪运动模拟算法

为了模拟海面的运动效果，须将分形海浪生成点的波高设为与时间相关的函数，使其随着时间变化产生运动效果，具体实现算法如下:

在八级海浪的情况下，经过第七次迭代其效果如图3所示。

图3 八级海浪的第七次迭代效果图

3.4 提高海浪运动模拟效果的OpenGL方法

3.4.1 纹理映射技术

纹理映射是将一个纹理图像映射到三维物体表面来模拟景物表面细节的方法，是真实感图形生成的有效途径。实时模拟海浪波动效果时，如果对所有质点都使用FBM方法生成进行模拟，那么当前的PC机性能无法同时保证模拟出的海浪效果的真实性和实时性。为此使用了具有四方连续性的海浪图像作为纹理源贴到生成的每个正方形上。如图4所示，这样不仅可以有效地提高模拟效果的真实感，还能大大减少计算量，提高模拟的实时效果。

图4 纹理映射技术生成的三维海浪表面

这里采用的方法是使用OpenGL中的gl_Teximage2D()和glEnable(GL_TEXTURE_2D)函数来实现纹理映射。

3.4.2 源纹理拉伸技术

在使用纹理映射时，由于源纹理图像的大小是固定的，但是使用随机中点位移算法的菱形方形细分法生成的分形海面时由多次迭代生成且大小不一的正方形构成，这些正方形大小与源纹理图像大小不一定相同。这里使用了OpenGL中的glTexParameteri(GL_TEXTURE_2D，GL_TEXTURE_MIN/MAG_FILTER，GL_LINEAR)函数解决了这个问题，如图5所示，当源纹理图像大于映射的正方形时使用MIN参数，反之则使用MAG参数。

图5 源纹理拉伸技术生成的三维海浪表面

3.4.3 双缓冲技术

双缓冲区的窗口执行绘图命令实际上是在画面以外建立一个场景，然后很快地交换到窗口视图中。OpenGL中使用双缓冲技术，使用函数glutSwapBuffers()交换缓冲区，将图形缓冲区内容交换到当前画面显示缓冲区.图形缓冲区和当前画面缓冲区的显示数据交替出现，这种方式可以减少单一当前画面缓冲区由于计算延迟产生的闪烁现象，能有效地提高模拟效果。

3.4.4 OpenGL 显示列表

采用显示列表方式绘图一般要比瞬时方式快，尤其是显示列表方式可以大量地提高网络性能，即当通过网络发出绘图命令时，由于显示列表驻留在服务器中，因而使网络的负担减轻到最小。另外，在单用户的机器上，显示列表同样可以提高效率。因为一旦显示列表被处理成适合于图形硬件的格式，则不同的OpenGL实现对命令的优化程度也不同。

3.4.5 雾化效果

雾化是一种模拟自然界中雾气对场景物体视觉效果产生影响的图形绘制技术。此技术从视点到物体逐渐将物体的绘制颜色淡化，直至背景色。通过雾化处理可较好的表现出物体到视点的距离感。虽然雾化的具体计算非常复杂，但在OpenGL中的使用相关函数进行处理却非常简单。

3.5 海浪运动模拟的实现及结果分析

通过采用点高度值替换的方法可以比较好的模拟现实中的海浪运动的效果，既把后一点的高度值替换前一点的高度值，这样就可以实现海浪的向前推进和海浪具有波动的效果，达到了比较好的实现效果。

4 结论

本文理论主要源于分形几何学，以分数布朗运动数学模型为基础，进行分形三维海浪表面的建模和分形海浪运动仿真生成技术的研究和应用，通过对海浪的具体形态分析，得出了海浪的分形特征。根据FBM方法中的随机中点位移算法，具体采用菱形—方形法，生成了海浪分形曲面。在分形海浪的建模过程中，采用二维高斯随机插值算法，进行随机分形海浪，实现海浪的分形。其次海浪的运动形态可以看作是由一系列具有不同频率、波数、波高和传播方向的规则波叠加而以分形理论为基础，依据高度迭代方式，实现分形海浪的运动，并根据具体海浪运动特点，结合风力对海浪运动效果的影响，同时采用纹理映射技术、源纹理拉伸技术、双缓冲技术、OpenGL显示列表、雾化效果等OpenGL方法提高海浪模拟效果的真实性和实时性，以Visual C++为开发平台，通过调用OpenGL的接口函数进行二次开发，实现了对三维海浪运动的计算机模拟，较好地实现了海浪运动的效果。

本课题虽然实现了三维真实感的海浪的场景构造，但是对于构建完备的三维浪花而言，仅仅是完成了该系统的基础性建模和真实感科学算法的实现过程，这些工作为构建完备的三维浪花系统打下了坚实的基础。在此基础上，应该加大对自然海浪的特征的研究，采用多种数学模型，以求满足构建各种自然海浪的需要。

［1］曾文曲，王向阳.分形理论与分形的计算机模拟.沈阳:东北大学出版社，2001.1 －102.

［2］黄心渊.虚拟现实技术与应用.北京:科学出版社，1999，7.

［3］刘浩，戴居丰，杨磊等.虚拟现实技术及其应用研究.微计算机信息，2005，21(1):200 －201.

［4］BAENSLEY M F.Fractal Everywhere［M］.New York:Academic Press，1993.

［5］吴斌，段海波，薛凤武.OpenGL编程权威指南.中国电力出版社，2001，8.

［6］孙博文.分型算法与程序设计——Visual C++实现［M］.北京:科学出版社，2004.

［7］BAENSLEY M F.Fractal Functions and Interpolation［J］.Constructive Approximation ，1986，(2):203 －329.

［8］王子凡，林宗坚.基于图像表面积的分形布朗运动分数维算法研究［J］.武汉大学学报，2005，30(2):161 －165

［9］王琰，曾兰玲.基于分形的三维竹子算法［J］.中国图像图形学报，2007，12(1):177 －182.