互模拟
——检验集合相等的一个新工具
姚从军
(湖南科技学院 思想政治理论课教学科研部,湖南 永州 425100)
互模拟
——检验集合相等的一个新工具
姚从军
(湖南科技学院 思想政治理论课教学科研部,湖南 永州 425100)
在ZFC-(AFA)系统中,外延公理不可强大得足以判断两个非良基集合是否相等。因此随着研究范围的扩大,需要新的理论解决新问题。为解决非良基集合相等问题,文章介绍了四个方法:图理论方法、互模拟方法、游戏方法和方程法,这几种方法最后都可以归结为互模拟方法。故互模拟是检验集合相等强有力的工具。
外延公理;非良基集合;可及点图;互模拟;游戏;解引理
在ZFA公理系统中,根据外延公理可知:两个集合相等当且仅当它们有共同的元素。因此,要判断两个良基集合是否相同,只需通过观察看看它们的元素是否相同即可。但是在ZFC-(AFA)系统中,对于两个非良基集合而言,外延公理不可强大得足以判断它们是否相等。例如 A={B},B={A},是否相等,根据外延公理,会得出 A=B当且仅当B=A这样的循环定义,这就需要研究新的方法,从而可以判断非良基集合是否相等。
一 图理论法
(一)图的装饰判断法
集合论中,最初人们为了定义良基集合的相等,使用了外延公理,但是由于非良基集合的存在,用已有的经典外延公理无法断定两个非良基集合的相等性,为解决这一问题,集合的图理论首先产生,用可及点图刻画集合。公理AFA假定每个图有唯一装饰。这里存在两个重要事实,装饰的存在性和唯一性。前一个事实告诉我们非良基集合存在,因为非良基图的存在是一个不争的事实,而依据AFA,非良基图也应该有一个装饰,根据可及点图理论这个装饰不可能是良基集合,所以必然是非良基集合,这样由非良基图的存在,我们就得出非良基集合的存在性。后一个事实告诉我们什么样的非良基集合是相等的,因为据AFA,每个图的装饰是唯一的,所以如果两个集合可有效地指派到同一个图的同一个结点,则这两个集合是相等的。AFA告诉我们每个图只是一个唯一集合的图,装饰同一个图的所有集合在此理论下都是相等的集合。[1]例如集合Ω={Ω}、A={B}和B={A}是相等的,因为下图有一个装饰,其中两个结点都指派Ω,并且还有一个装饰,其中左边的结点指派A,右边的结点指派B。
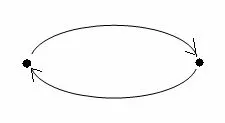
所以我们可得出集合相等的一个判断方法:两集合相等,如果它们是同一个集合的图,或者可装饰同一个图的同一个结点。
(二)图之间的互模拟关系判断法
但是一个集合可用不同的可及点图来刻画,[2]例如,集合2能够用下列图刻画:

我把这种刻画同一个集合的各种图称为等价图(模型等价),并将这种模型等价性称之为装饰等价性,因为它们是同一个集合的图,或者说它们有相同的装饰。
那么刻画同一个集合的不同图之间有什么必然联系呢?结论是两个图等价当且仅当它们具有互模拟关系。Aczel给出了可及点图理论中的互模拟具体表现形式,他说,系统M上的一个二元关系R是M上的一个互模拟,如果R⊆R+,这里对于a,b∈M(aM 和bM 分别指结点a、b的子结点集)
aR+b⇔∀x∈aM∃y∈bMxRy∧∀y∈bM∃x∈aMxRy[3]
既然具有互模拟关系的图刻画同一集合,那么所有具有互模拟关系的可及点图所刻画的集合都是相等的集合。例如,已知一个集合s={s},我们用下图来描述这个集合,这里用s装饰结点n。
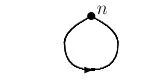
再给予一个结合t={t},我们想判断s和t是否相等。如果仅仅根据外延公理,我们无能为力,因为外延公理断定两个集合相等仅当它们有相同的元素,而集合s和t只有自身是自己的唯一元素,无法断定它们的相等性。未解决这一问题,我们必须另辟蹊径,我们画出集合t的可及点图如下,这里用t装饰n′。

现在我们来检验集合s和t的图是否具有互模拟关系,很显然两个图之间存在一个互模拟关系R={(n,n′)。最后根据图理论可知,在非良基集合论中,集合s和t就是相等的集合。
实际上这是一种间接互模拟判断法。这样就找到了刻画集合相等的强外延公理:两个集合相等,当且仅当它们的可及点图是互模拟的。这也说明了过去的外延公理,即两集合相等,当且仅当它们有相同的元素只是判断两集合相等的充分条件。也就是说,如果两集合有相同的元素,那么它们必然相等;但是两集合相等不蕴涵它们有相同的元素。因此外延公理不是判断两集合相等的必要条件。
二 直接互模拟法
一个关系 R是集合上的一个互模拟关系当且仅当对所有的集合s和t,如果(s,t)∈R那么
·对∀s′∈s,∃t′∈t使得(s′,t′)∈R,并且
·对∀t′∈t,∃s′∈s使得(s′,t′)∈R
两个集合s与t是互模拟的当且仅当存在一个互模拟关系R使得(s,t)∈R。
两个集合s与t相等当且仅当它们是互模拟关系的。[2]
三 游戏法
运用两个集合S和T玩游戏,你是正方,即认为S和T相等,对方称反方,认为S和T不相等,对方先从两集合中任一集合(比如 S)中找出一个元素 X,断言 X不是 T的元素,即不与 T的任一元素相等。你表示反对,并从 T中找出一元素Y,声称Y=X。现在你们再用XY玩游戏,如此进行下去。如果在某一点(如 Xˊ、Yˊ),反方找到一个Xˊ的元素X〞,而你从Yˊ中找不出元素与之相匹配,这时就表明反方赢了,因此S与T不相等,在其他两种情况下:
(1)反方不能再前进一步,即反方每动一步,你均能找到匹配步,最后反方不可再动。(2)双方可以无限地玩下去,无穷无尽。
表明你赢了,即S与T相等。
在游戏中,可得出结论:S与T相等当且仅当你有赢的战略。这种方法其实是互模拟的间接运用,因为你有赢的战略,当且仅当S和T是互模拟的,再根据方法2,当且仅当S与T相等。[4]
四 方程解引理法
运用图描述集合的一个择换方法是运用方程描述集合,比如Ω是满足x={x}的唯一集合x,这说明可用x={x}来定义集合Ω。由于方程涉及到未定元,所以我们在集合中引进本元与之对应,令x是任一未定元,x的一个方程系统是满足如下条件方程类:
对每个x∈X,恰有一个形如x={x1,x2,-------}的方程,其中{x1,x2,-------}是 x的子集。我们用(x=Sx)x∈X表示X方程系统,如 x={x,y},y=Ø是{x,y}方程系统。一个方程系统的解是一个函数δ,它对每个 x∈X指派一个集合使得δx={δy|y∈Sx}。集合{δx|x∈X}称为该方程系统的解集。
图与方程系统紧密相关,已知一个图,我们把图中结点看做未定元,并且对任一结点x,令x=Sx是一方程,其中S是以结点 x的后继为元素的集合,这样就得到一个方程系统;相反,已知一个X方程系统,我们把X中的未定元看做结点,并且令x,y∈X,x→y当且仅当y∈Sx,这样我们就得到一个图。我们设该方程的解为δ,与之对应的图的装饰是{δx|x∈X}。在每一个方向,一个给定方程系统的解δ指派给X中任一未定元x的集合δx,与对应的图装饰d指派给结点x的集合dx相同,两个不同类模型建立了对应性,并且图与对应的方程系统都是同一集合的模型。由于每个图有唯一装饰,则相应可得到每个方程系统有唯一解。故 X方程系统与 Y方程系统等价,当且仅当它们的解集相同。而解集是集合,两个集合相同当且仅当它们是互模拟的,所以两个解集相同当且仅当它们是互模拟的。由方程系统与图的对应性和每个图都是一个集合的图理论可知,这两个方程系统也是分别刻画某个集合的方程系统,故两个集合相等当且仅当刻画它们的方程系统有相同的解集,当且仅当对应的方程系统的解集是互模拟的。[5]
刻画集合相等还有其它的方法,这里不一一列举。上面四种方法有一个共同点,那就是均直接或间接用到互模拟,也就是这四种判断集合相等性方法最后都归结为判断不同类对象间的互模拟性,这从另一个方面反应了互模拟在理论上的应用价值,它是判断集合相等性的强有力的工具。
[1]Davide Sangiorgi.On the origins of Bisimulation,Coinduction,and Fixed Points[J].Tcchnical Report UBLCS-2007-24,October 2007.
[2]Jelle Gerbrand. Bisimulations on Planet. Kripke[D].PhD thesis ,insititute for logic,Language and Computation.University of Amsterdam,1998:5-6.
[3]P.Aczel.Non-Well-Founded Sets[M].Stanford: CSLI,1988:20-26.
[4]Van Benthem Modal logic for open minds[M].Stanford:CSLI Publications, 2005:30-34.
[5]J. Barwise, L. Moss. Vicious Circles: On the Mathematics of Non - Well –Founded Phenomena[M]. Stanford: CSLI,1996:77-83.
B815.1
A
1673-2219(2011)03-0088-02
2010―10―08
姚从军(1971-),男,湖北随州人,哲学博士,讲师,研究方向为现代逻辑。
(责任编校:周 欣)

