不同晶系应变Si状态密度研究*
宋建军 张鹤鸣 戴显英 宣荣喜 胡辉勇 王冠宇
(西安电子科技大学微电子学院,宽禁带半导体材料与器件重点实验室,西安 710071)(2010年3月18日收到;2010年8月6日收到修改稿)
不同晶系应变Si状态密度研究*
宋建军 张鹤鸣 戴显英 宣荣喜 胡辉勇 王冠宇
(西安电子科技大学微电子学院,宽禁带半导体材料与器件重点实验室,西安 710071)(2010年3月18日收到;2010年8月6日收到修改稿)
应变Si技术是当前微电子领域研究发展重点,态密度是其材料的重要物理参量.本文基于应力相关KP理论,建立了(001),(101)和(111)晶面施加双轴应力形成的四方、单斜及三角晶系应变 Si导带、价带态密度模型.结果表明,除单斜和三角晶系导带底态密度外,应力对其余各态密度均有显著影响.本文所得模型数据量化,可为应变Si材料物理的理解及其他物理参数模型的建立奠定重要理论基础.
应变Si,KP,态密度
PACS:71.20.- b,71.15.- m,71.20.mg
1.引 言
应变Si是当前国内外研究发展重点,在高速/高性能CMOS器件和电路,以及光电子器件中有广阔的应用前景[1—3].由于晶格失配,弛豫 Si1-xGex衬底上可外延获得应变Si,且不同晶面衬底对应不同晶系应变Si.典型的晶面(001),(101)和(111)分别对应形成四方、单斜和三角晶系应变Si.
态密度是应变Si重要物理参数,其研究可为应变Si材料物理的理解及其他物理参量(如有效状态密度、载流子散射机理等)模型[4]的建立奠定重要理论基础.然而,到目前为止,有关应变Si态密度的文献仍缺乏报道.有鉴于此,本文采用应力相关KP理论,基于所得导带底电子和价带顶空穴态密度有效质量,进一步建立了四方、单斜和三角三个不同晶系应变Si的导带、价带态密度与应力(由Ge组分表征)的量化解析模型.结论所含立方晶系未应变Si(Ge组分x为0时)导带底电子和价带顶空穴态密度有效质量及导带底和价带顶附近态密度模型与文献报道一致[5],间接说明了本文结果的正确性.
2.模型建立
与立方晶系未应变 Si材料类似,四方、单斜和三角晶系应变 Si导带底、价带顶附近态密度模型(gc(E),gv(E))如下:

式中,EC,EV分别对应四方、单斜和三角晶系应变Si导带底能谷、价带顶带边能级,其值参见文献[6—9];V是应变Si材料的体积分别是导带底电子、价带顶空穴态密度有效质量.
弛豫 Si1-xGex衬底 Ge组分较低(≤0.4)时,晶格失配引起外延应变Si层的应变可视为微扰,即应变Si材料体积V在应力的作用下变化不大,可近似取未应变Si体积.其正确性由应变Si晶格常数的分析得以证实[10,11].因此,进一步建立导带底电子、价带顶空穴态密度有效质量模型)便成为获得应变Si材料导带底、价带顶附近态密度的关键.
为此,本文采用应力相关KP微扰理论,首先建立了四方、单斜和三角晶系应变 Si导带、价带结构模型,包括其导带能谷劈裂能(ΔEC,Split)、价带带边劈裂能(ΔEV,Split)及电子、空穴的有效质量与 Ge组分(x)的关系模型[7—9,12,13].考虑应变 Si导带能谷简并度(简并度由a和b表征,四方晶系应变Si a与b分别为2和4;单斜晶系应变Si a,b分别取4和2;三角晶系应变 Si a与 b分别为6和0)[6],基于已建能带结构和载流子有效质量模型,采用类似 GaAs系统处理方法最终建立了应变Si导带底电子、价带顶空穴态密度有效质量模型[14],
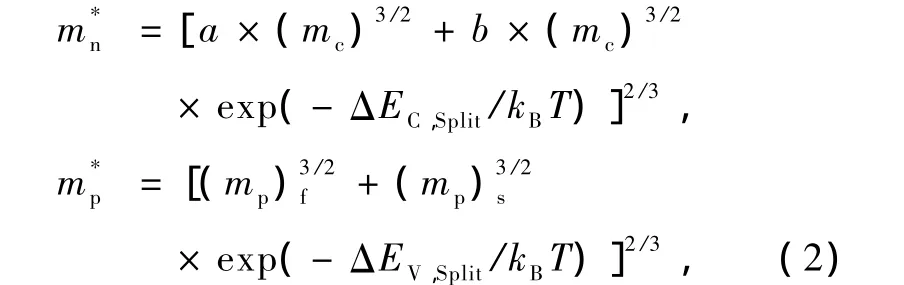
3.模型讨论
图1—图6所示分别为300 K时四方、单斜和三角晶系应变Si导带底、价带顶态密度与能量(E)及应力(由Ge组分x表征)的理论关系.由图可见,四方、单斜和三角晶系应变Si导带底、价带顶态密度与能量(E)均为抛物线性关系.除单斜和三角晶系导带底态密度外,应力对其余各态密度均有显著影响.尤其是四方晶系应变Si,无论是导带底还是价带顶态密度,其值在Ge组分低于0.2时均随着Ge组分(应力)的增加而显著减小.之后,虽然应力继续增大,而其变化却不大.应变 Si材料有效状态密度及各载流子散射机构与态密度密切相关,基于所得态密度模型,可为以上模型建立奠定重要的理论基础.

图1 四方晶系应变Si导带态密度
四方、单斜和三角晶系应变 Si态密度不同于立方晶系未应变Si的物理现象可解释为,Si材料所属晶系不同,相应的能带结构及载流子有效质

图2 四方晶系应变Si价带态密度
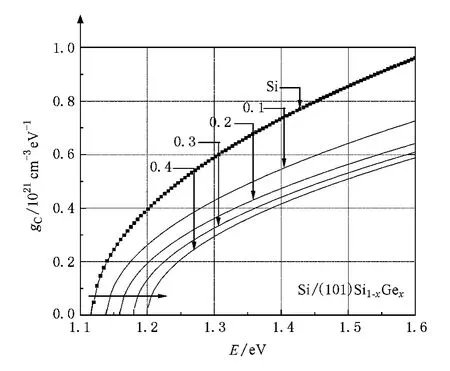
图3 单斜晶系应变Si导带态密度
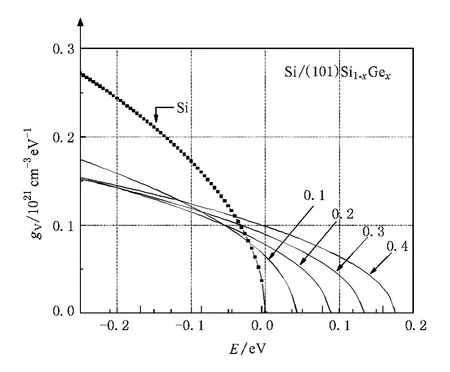
图4 单斜晶系应变Si价带态密度
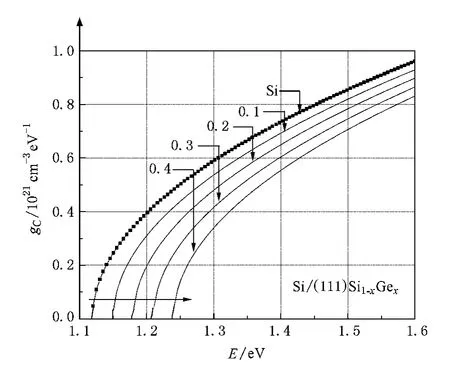
图5 三角晶系应变Si导带态密度
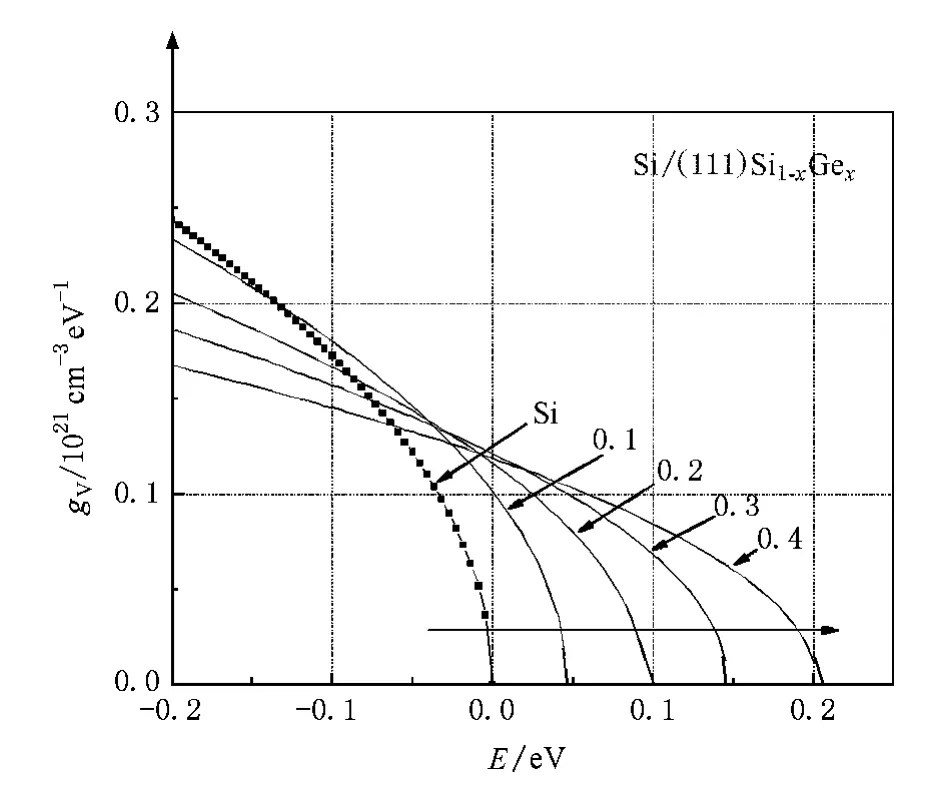
图6 三角晶系应变Si价带态密度
量不同,即导带底电子、价带顶空穴态密度有效质量不同.态密度有效质量是决定态密度的本质因素.正是由于四方、单斜和三角晶系应变 Si导带底电子、价带顶空穴态密度有效质量不同于立方晶系未应变Si,其态密度必然发生相应变化.值得一提的是,应力对单斜和三角晶系应变Si的导带底状态密度影响很小,这主要是由于应力没有引起三角晶系应变Si导带能谷的分裂,其导带底仍为6度简并能谷.虽然应力使得单斜晶系应变Si导带底能谷发生分裂,但由于其导带底为4度简并能谷,故单斜晶系应变Si导带底态密度变化不如四方晶系应变Si变化显著.
此外,各晶系应变Si材料导带底能谷(EC),价带顶带边能级(EV)随应力Ge组分的变化在图上也有体现.综合EC,EV二者的变化,可进一步获得各晶系应变Si材料禁带宽度随应力变化的情况.值得一提的是,基于本文模型还可获得立方晶系未应变Si(Ge组分x为0时)导带底和价带顶附近态密度,本文所得结果与文献报道结果一致,据此可以间接说明本文四方、单斜和三角晶系应变Si态密度模型的正确性.
4.结 论
态密度是应变Si材料的重要物理参数,其研究可为应变Si材料物理的理解及其他物理参量模型的建立奠定重要的理论基础.有鉴于此,本文采用应力相关KP理论,基于所得导带底电子和价带顶空穴态密度有效质量,进一步建立了四方、单斜和三角三个不同晶系应变Si的导带、价带态密度与应力(由Ge组分表征)的量化解析模型.
结果表明,四方、单斜和三角晶系应变 Si导带底、价带顶态密度与能量(E)均为抛物线性关系.除单斜和三角晶系导带底态密度外,应力对其余各态密度均有显著影响.尤其是四方晶系应变Si,无论是导带底还是价带顶态密度,其值在Ge组分较低时均随着Ge组分(应力)的增加而显著减小.之后,虽然x继续增大,而其变化却不大.此外,基于本文模型可以得到立方晶系未应变Si(Ge组分x为0时)导带底和价带顶附近态密度,本文所得结果与文献报道结果一致,据此可以间接说明本文四方、单斜和三角晶系应变Si材料态密度模型的正确性.
[1] Phama A T,Jungemann C,Meinerzhagen B 2008 Solid-State Electronics 52 1437
[2] Jiang T,Zhang H M,Wang W,Hu H Y,Dai X Y 2006 Chin.Phys.15 1339
[3] Chang S T,Liao S H,Lin C Y 2008 Thin Solid Films 517 356
[4] Smith R A 1978 Semiconductors(London:Cambridge University Press)p116
[5] Liu E K,Zhu B Sh,Luo J Sh 1994 Semiconductor Physics(Beijing:Defense Industry Press)p52(in Chinese)[刘恩科、朱秉升、罗晋生1994半导体物理学(北京:国防工业出版社)第367页]
[6] Song J J,Zhang H M,Hu H Y,Dai X Y,Xuan R X 2007 Chin.Phys.16 3827
[7] Song J J,Zhang H M,Dai X Y,Hu H Y,Xuan R X 2008 Journal of Semiconductors 29 1670(in Chinese)[宋建军、张鹤鸣、戴显英、胡辉勇、宣荣喜2008半导体学报 29 1670]
[8] Song J J,Zhang H M,Dai X Y,Hu H Y,Xuan R X 2010 Journal of Semiconductors 31 1670(in Chinese)[宋建军、张鹤鸣、戴显英、胡辉勇、宣荣喜2010半导体学报 31 1]
[9] Song J J,Zhang H M,Dian X Y,Hu H Y,Xuan R X 2009 Research&Progress of SSE 29 14(in Chinese)[宋建军、张鹤鸣、戴显英、胡辉勇、宣荣喜 2009固体电子学研究与进展 29 14]
[10] Song J J,Zhang H M,Dian X Y,Hu H Y,Xuan R X 2008 Acta Phys.Sin.57 5918(in Chinese)[宋建军、张鹤鸣、戴显英、胡辉勇、宣荣喜 2008物理学报57 5918]
[11] Song J J,Zhang H M,Hu H Y,Fu Q 2009 Science In China(G)52 546
[12] Song J J,Zhang H M,Xuan R X,Hu H Y,Dian X Y 2009 Acta Phys.Sin.58 4958(in Chinese)[宋建军、张鹤鸣、宣荣喜、胡辉勇、戴显英 2009物理学报58 4958]
[13] Song J J,Zhang H M,Hu H Y,Xuan R X,Dian X Y 2009 IEEE International Conference on Electron Devices and Solid-State Circuit Xi'an
[14] Shi M,Wu G J 2008 Physics of Semiconductor Devices(Xi'an:Xi'an Jiaotong University Press)(in Chinese)p389[施 敏、伍国珏2008半导体器件物理(西安:西安交通大学出版社)第389页]
PACS:71.20.- b,71.15.- m,71.20.mg
Densities of states of strained Si in different crystal systems*
Song Jian-Jun Zhang He-Ming Dai Xian-Ying Xuan Rong-Xi Hu Hui-Yong Wang Guan-Yu
(Key Lab of Wide Band-Gap Semiconductor Materials and Devices,School of Microelectronics,Xidian University,Xi'an 710071,China)(Received 18 March 2010;revised manuscript received 6 August 2010)
There has been aroused a lot of interest in the strained Si technology in the microelectronic field.Density of states(DOS)is an important physical parameter in strained Si materials.Based on the Kleinert's Variational perturbation(KP)theory related to stress,DOSs of electrons and holes near the bottom of conduction band and the top of valence band are obtained in tetragonal,rhombohedral and monoclinic strained Si grown from(001),(101)and(111)substrates respectively.It is found that their DOSs are obviously different from the ones of cubic unstrained Si,except DOSs of electrons near the bottom of conduction band in rhombohedral and monoclinic strained Si.The quantized model obtained can provide valuable references for understanding the strained Si material physics and developing the theoretical model of the other important physical parameters.
strained Si,KP,density of state
*国家部委项目(批准号:51308040203,9140A08060407DZ0103,6139801),高校基本科研业务费项目(批准号:72105499,72104289)资助的课题.
E-mail:wmshhsong@tom.com
*Project supported by the National Ministries and Commissions(Grant Nos.51308040203,9140A08060407DZ0103,6139801),the Fundamental Research Funds for the Central University(Grant Nos.72105499,72104289).
E-mail:wmshhsong@tom.com

