数学建模优化程序设计与数学原理的综合运用

王福来

浙江财经学院数学与统计学院 浙江杭州 310018

☆课程建设与实践教学☆

数学建模优化程序设计与数学原理的综合运用

王福来

浙江财经学院数学与统计学院 浙江杭州 310018

从符号与数值的转化、同余映射中的周期长度及分阶段执行程序等3个方面，以实际例子研究了如何在实践中运用数学原理来优化程序设计、节约运行时间，达到利于解决数学建模问题的目标。

数学建模；优化程序设计；数学原理

数学建模中程序设计与数学原理的综合运用往往直接涉及实践中目标能否实现。数学建模中经常涉及程序的编制,如果程序的编制过于复杂,往往会使系统运行时间过长,甚至无法运行,严重妨碍数学建模问题的解决。其中一个主要的原因是程序设计中没有尽量考虑用数学原理来优化程序,使程序得到简化、优化。

笔者分别从3个方面来论述如何用数学原理优化程序设计：(1)通过符号与数值的转化以有效确定序列的大小及距离；(2)根据数论知识解决同余映射中周期长度对初值的依赖性；(3)分阶段执行程序以验证程序的灵敏性或系统的稳定性。

1 用数学原理优化程序设计的几种方法

1.1 比较子序列大小的问题

我们知道数学模型中经常要处理一些符号问题。如在Lorenz映射中,人们为了计算复杂度、排列熵等指数,经常利用符号动力学方法得到一列符号数据,这时往往需要比较子序列的大小。它的比较方式是,任给两个符号序列,它们的大小排序为：

这里, ∑为两个符号序列的公共字头。

这个比较在程序设计时是较为方便的,如果把它们先转化为二进制数据则更能节省时间。但另一些情况下就不会这么简单。例如,投掷硬币实验出现正面、反面,得到一个随机序列,如001011101……,如果简单地把符号与十进制或二进制数值等同,这是没有意义的。但在数学建模中有时我们仍然可利用符号与数值的转化关系达到优化程序设计的目的。

为了计算两个点12( )xx…与12( )yy… 间的距离,一般的文献采用如下两种距离定义方式：

以上两个式子都表明,两个符号序列,如{a1a2… am}与{b1b2… bm},前面符号重复得越多,则两个序列之间的距离越近。但若按照这种距离公式直接比较两个子序列的每个符号,则会占用太多的计算机机时,甚至是不可能完成的。

现在我们采用下面的数学处理方法,则会兼顾到这两方面,即既可以保留原来的顺序关系,又可以在程序上(用Matlab语言)节约计算机机时。

方法是：

Step1：用num2str()函数把符号串{a1a2… am}转为字符串{a1a2… am},如num2str(1010)＝1010,等式右边的1010不再是符号而是二进制字符串。

Step2：用bin2dec()函数将Step1中的二进制数据，设为xi(i=1,2，…，n) 转化为十进制的数据yi(i=1,2，…，n)。

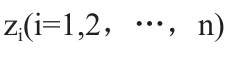
它的数学原理是：原来的序列,如{1 011},{1 001},{1 010},虽然它们之间并无顺序关系,但赋予了顺序关系后,并不妨碍原来的距离关系。这样就利于程序执行了,显然这种方法可以大量节约程序的机时。

1.2 同余映射中周期长度的问题

密码学中经常用同余映射(4)来模拟同余映射(5),以获得类似于(4)的混沌轨道：

同余映射(5)在 z＞ 1时为混沌映射,且李雅普诺夫指数为lnz。(l0,z,m)称作密钥。对每一个特定的数字混沌映射,都需要利用数论和遍历性理论等专门的数字工具进行独立的研究。例如,对于映射(4),当 z= 2且m= 2k−1时周期 P(m)取得最小值 P(m )= [l nln m]+1；当m为素数且z为一个乘法群的生成元时,P(m)取得最大值 m− 1；而当m为其他数时,P(m)的典型值为多少却不得而知。事实上,当(l0,z,m)分别取(37,6,3989)，(37,29,3989),(37,2,3989)时,得到的最长周期的轨道长分别为997,1994,3998,而不是都为 P(m )= m−1。因此用文献[3,4]的方法生成的周期轨道有时不够长,周期轨道长度变化较大,这是生成伪随机序列的主要缺点。另一方面,m越大,则素数分布的密度越小。这往往使m取得相当大,而这使得计算机达不到要求,某些程序无法执行,也使得作为参数空间的密钥(l0,z,m )非常有限,给通信密码造成不利。事实上在程序编制时,只要加入一些数学思想则可以完全避免这个问题,即使得对任意模为m(m为素数,m ＞ 2)的同余映射(4)都可以构造出相应的长度为 m−1的不稳定周期轨道。具体步骤是：

Step1：对任意素数m和任意整数z(z ≥ 2),任取l0(2 ≤ l0≤ m − 1),由(4)生成集合 A0；

Step2：若 A0= {1 ,2,… ,m −1},则已实现目标；否则取{1 ,2,… ,m −1}A0中的最小数作为l1,回到Step1。设由Eq.4生成集合为 A1。

Step3：重复执行Step1 和Step2直到第n步产生的集合A0∪A1∪…∪An= {1,2,… ,m −1},则A0∪ A1∪ … ∪An的 长度必为 m−1。

上述步骤的数学原理是： A0,A1,… ,An的任两个集合必不相交,因为否则由数论中的同余理论,这两个集合是相同的,这与Step1与Step2的设置相矛盾。

1.3 分阶段执行程序

执行一个复杂的程序(为表达方便,这里称为总程序)时,往往需要更改其中的参数空间的一个或几个参数反复运行,以检测系统的稳定性、模型的灵敏性或数据的某些特征。这时会遇到两种情况：(1)有些程序的子模块是不变的,反复运行是没有必要的,占据了较多计算机机时；(2)里面有随机生成函数,每次运行它都会自动生成新的数据,而更改的参数又需要在与前一次不变的随机数下运行,这就达不到检验的目的。

解决这两个问题的最好方法是分阶段执行程序,即分两个或多个子程序执行,具体来说,分下面两个步骤：

Step1：将只生成数据而不需要更改参数的子程序(一般是总程序的前部分,记为ProgramⅠ)单独执行；将生成的变量保存起来,如将生成的数据集合设为A,再将A保存到某个根目录下,语句是：save('E:mydata1. mat','A')。当然有多个数据集合,可保存多次。

Step2：另编辑一个程序,在程序的开头用语句load(' E:mydata1.mat ')将ProgramⅠ中的变量下载,并将总程序的其余部分置于其后。这样的形成的程序记为Program Ⅱ。于是要更改参数,则只需要更改ProgramⅡ中的参数就可以。

2 结束语

通过实例说明了编制程序要考虑到实践中可行性问题。这方面的例子还可以参考笔者的文章[5]。在具体的建模中要养成将数学原理运用到程序设计中去的思维习惯,不仅可节约时间,使程序可以运行,同时也提高了程序的质量,利于修改和进一步编辑,以达到实践的目标。

[1] 罗卫民,李昌兴,史克刚.“数学实验”与“数学建模”课程教学改革[J].高等工程教育研究,2005,6：110～112

[2] 李国斌.微分方程解实际问题的探讨[J].高等教育研究,2009,24(2)：62～63

[3] Sánchez S, Criado R.and Vega C. A generator of pserdo-random numbers sequences with a very long period. Mathematical and Computer Modeling. 2005, 42(7)：809～816

[4] 王蕾,汪芙平,王赞基.一种新型的混沌伪随机数发生器[J].物理学报,2006,55：3964～3975

[5] Wang Fulai 2010 Determining consecutive periods of the Lorenz maps. Advances in Difference Equations. Doi:10.1155/2010/985982 Article ID 985982.

Optimizing and integrating program designing and mathematical principles in mathematics modeling

Wang Fulai
Zhejiang university of f nance and economics, Hangzhou, 310018, China

With three examples of transformation from symbols to numbers, periodic lengths of congruence and performance in steps, optimization program designing by integrating mathematical principles is studied to save runtime and solve problems in mathematical modeling.

mathematical modeling; optimization of program designing; mathematical principle

2011-03-23 稿件编号：1103158

王福来，博士，副教授。

2010年浙江省新世纪高等教育教学改革项目(编号：ZC2010052)；浙江财经学院一类课程建设项目（编号：xjy1200915）。