大学物理实验中关于不确定度的几个问题讨论
高 建刘 伟马续波
1.高等教育出版社 北京 100029 2.华北电力大学数理系 北京 102206
大学物理实验中关于不确定度的几个问题讨论
高 建1刘 伟1马续波2
1.高等教育出版社 北京 100029 2.华北电力大学数理系 北京 102206
主要讨论了大学物理实验误差和不确定度的关系以及直接测量不确定度的评估,最后对单次测量的不确定度评估以及不确定度计算过程中数据修约问题进行了讨论。
大学物理实验;不确定度;误差
Abstract: Uncertainty in university physics experiment and its relationship with error were discussed, besides how to assess the uncertainty of direct measurement. And it also discusses the assessment of the uncertainty in one-time measurement and how to revise the data during the process of calculate uncertainty.
Key words: university physics experiment; uncertainty; error
大学物理实验是高等理工科院校学生进行科学实验基本训练的重要基础课程之一。测量误差与不确定度是大学物理实验中两个非常重要的概念。误差理论已经较为成熟,而不确定度的概念、理论和应用规范等尚在不断明确、发展和完善之中。教学实践证明:不确定度更能全面反映测量结果的可信程度,大学物理实验中有关测量结果的评定,还应以不确定度概念为主,以误差概念为辅。物理实验的结果表述同不确定度的概念一样,在大学物理实验中占有很重要的地位。通过教学实践发现,学生对测量误差和不确定度概念的联系与区别理解得并不是很清楚,所以笔者首先讨论了误差与不确定的联系与区别,接着对单次测量的不确定度评估、不确定度计算过程中数据修约问题进行了讨论。
1 误差与不确定度的联系与区别
实验中所得的测量值,因受到被测对象、周围环境、所用仪器、测量方法以及测量者等种种因素的影响,会使之偏离真值而产生误差。根据误差所产生的原因和性质,可将其分为系统误差和随机误差(又称偶然或统计误差)。不确定度表是指由于测量误差的存在而对被测量值不能肯定的程度,它表征被测量的真值在某个量值范围的评定,反映了测量结果的可信程度的高低。
随着现代计量学的发展和进步,误差理论体系也愈加趋于成熟和完善。不过误差理论尚存在两个方面的缺欠:(1)误差按其性质分为系统误差和随机误差,这种分类方法既不够严密,也不够科学。因为在很多情况下,这两种误差紧密相关且没有截然分明的界线,在一定条件下相互转化,所以在实际测量中,就往往会造成误差属性判断问题的困难。例如测量弹性模量的钢丝,由于制造和长期使用方面的原因,其截面不可能是严格的圆,因此在确定的钢丝位置,“直径”的测量表现为系统误差,但在不同的截面和位置,这种系统误差却又表现出某种随机性。(2)误差定义为测量结果与待测量真值的差值,它是一个理想的概念。由于真值永远不可知,所以任何一个确切的误差值同样是不可知的。实际上不管是系统误差还是随机误差,都只是根据测量资料所进行的推断和估计而已。因此,用误差来评估测量结果的可靠程度,必然会遗漏一些影响测量结果准确性的因素。而不确定度则是用以表示被测量的真值处于某一量值范围内的合理评价。不确定度是说明测量结果的一个参数,可理解为与一定置信概率相联系的误差分布宽度的一半。它由可用统计方法估算的A类不确定度分量UA和无法用统计方法估算的B类不确定度分量UB合成,这样就避免了用“统计”或者“随机”这样的语言造成的误解。不确定度理论的发展和完善并不是完全抛弃了误差理论,相反,不确定度的概念和体系是在现代误差理论的基础上发展起来的。对于描述理论和概念本身,误差理论是非常方便的,而对于需要给出数值和分析的情况,用不确定度表示则是更科学和合理的。
2 不确定的评估

为不确定度的合成。依据国家计量规范,通常是以95%的置信概率来评定的,由此得到的不确定度就为扩展不确定度。
2.1 A类不确定度的评估


表1 不同置信概率下的pt置信因子
在大学物理实验中,因为实验室测量条件较为稳定,在等精度有限次重复性测量情况下,为了避免繁琐的运算过程,统计不确定度UA的计算通常采取两种简化方案:

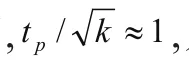
2.2 B类不确定度的评估
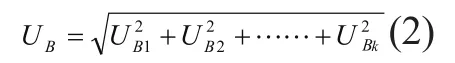


表2 常见分布类型与常数C值的关系
文献[4]就采用此式计算B类不确定分量。
3 单次测量的不确定度和计算过程中不确定度修约问题的讨论
对于因条件限制或者其他原因而只进行了一次测量,扩展不确定度可更为简单地取仪Δ≈U ,但这并不是说明(1)式中的UA不存在,UA其实是存在的,只是不能用贝塞尔公式算出,因为n=1时贝塞尔公式是发散的。单次测量时取仪Δ≈U ,并不说明只测一次时U小,而是因为这种估算是比(1)式更为粗略的估计方法。如用其他方法求得单次测量的UA以后再合成,所得结果的不确定度U将大于多次测量的值。
有效位数能在一定程度上反映量值的不确定度,数据修约应使最后测量结果的不确定度基本不会增大,不确定度决定有效位数。严格地说,要使读数、运算和修约等过程产生的附加误差限显著小于测量结果的扩展不确定度。为了使运算和中间过程的数据修约基本不会改变结果的总的不确定度,传统方法中给出了有效位数确定的规则。这些规则在计算工具比较落后的时代,对减少计算量,提高效率是很有帮助的,但在计算机普及以后就没有必要了。物理实验数据处理过程中,对参与运算的数和中间计算结果都可不做修约,可比传统方法估计的位数适当多取几位,只在最后结果表示前再做修约,这样更有利于实验效率的提高。所以在物理实验数字修约中注意做到抓两头,放中间即可。所谓抓两头,就是重视原始数据读取和最后结果表示;而放中间,就是中间运算过程中只要不无根据地减少运算前后的数据位数,多取几位也可行。
[1] 朱鹤年.基础物理实验教程—物理测量的数据处理与实验设计[M].北京:高等教育出版社,2003
[2] 刘才明.大学物理实验中测量不确定度的评定与表示[J].大学物理,1997,8:22~24
[3] 郭延生.大学物理实验的误差与不确定度[J].长春工程学院学报(自然科学版),2003,4:57~60
[4] 彭建,邓加军,师青梅.大学物理实验[M].北京:中国电力出版社,2008
Some discussions about uncertainty in university physics experiment
Gao Jian1, Liu Wei1, Ma Xubo2
1. Higher education press, Beijing, 100029, China 2. Physics department of north China electric power university, Beijing, 102206, China
2011-01-16 稿件编号:1101071
高建,博士,编辑。刘伟,博士,编辑。马续波,硕士,讲师。

