基于Fluent圆管内黏性流体流动的多媒体教学的应用研究
董金玲 李国威
辽宁工程技术大学 辽宁阜新 123000
基于Fluent圆管内黏性流体流动的多媒体教学的应用研究
董金玲 李国威
辽宁工程技术大学 辽宁阜新 123000
Fluent是流体力学中通用性较强的商业CFD软件。将Fluent软件引入流体力学多媒体教学中,可对定常不可压缩流体在圆管内流动进行数值模拟,分析流体层流、紊流的两种流动状态,验证管内流体速度及切应力分布。实践表明,在流体力学课堂上配以Fluent数值模拟,有助于学生消化较难理解的理论知识,增强学习兴趣,提高教学效果。
Fluent;多媒体教学;数值模拟;速度分布
Abstract: Fluent is a commercial CFD software with strong generality in the field of hydromechanics, and it was introduced in the hydromechanics multimedia teaching. Taking advantage of f uent, steady non-compressible f uid f owed in a tube was simulated. The two f ow state, laminar and turbulent, was analyzed. Fluid velocity and tangential stress distribution was validated. It proved that introducing f uent simulation in the class of hydromechanics can help students to understand theoretical knowledge, increase learning interesting, and improve teaching effects.
Key words: Fluent; multimedia teaching; numerical simulation; velocity distribution
流体力学是高等院校热能与动力工程等专业的一门专业基础课,其主要特点为抽象概念多,理论性强,数学基础要求高,实用性强。在初学这门课程时,理解基本概念,掌握理论知识,学会运用基本理论分析解决实际问题,常常是最重要也是学生难以达到的。而将Fluent数值模拟引入流体力学的多媒体教学中,可以模拟出不同条件限制下的流体运动,有助于学生理解流体的流动状态及运动规律。
Fluent为通用CFD软件包,用来模拟从不可压缩到高度可压缩范围内的复杂流动。在CFD软件中,Fluent软件是目前国内外使用最多、最流行的商业软件之一。同传统的CFD软件相比,Fluent具有稳定性好,适用范围广,精度高,可达二阶精度等优点。笔者应用Fluent软件对流体力学中的定常不可压缩流体在圆管内流动进行数值模拟,动态观测圆管内流体的流动现象,分析产生此现象的原因,使学生更为深刻地理解流体层流、紊流的两种流动状态。
1 圆管内黏性流体流动的相关理论
根据黏性流体的流动性质不同,可将其分为层流和紊流两种流动状态。对于不同的流动状态,流场的速度分布,产生阻力的原因、方式、大小等都不相同。
流体力学中利用雷诺数判定流体的流动状态,工程上一般认为雷诺数小于2320为层流,大于2320为紊流。研究定常不可压缩流体在圆管内的层流有2种方法,第一种方法是从N-S方程式出发,结合层流运动的数学特点建立常微分方程,第二种方法是从微元体的受力平衡关系出发建立层流的常微分方程。而研究湍流,唯一可行的方法是统计时均法。
1.1 利用N-S方程分析圆管内流体层流流动
因此N-S方程简化为:

1.2 利用统计时均法分析圆管内流体紊流流动
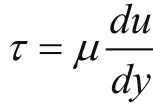
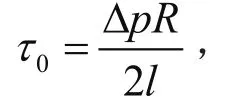
比较式(3)与式(6)可知,无论管内层流或紊流,过流断面切应力均成K字形分布,不过两者0τ不同,K字的斜率不同。
从上述推导管内层流与紊流速度分布公式可以看出学生要想掌握此章节,需要有较好的理论知识及数学基础。而运用Fluent模拟管内流体流动,可以很好地帮助学生理解流体的流动状态及管内流体的速度分布等知识。
2 圆管内黏性流体流动状态数值模拟与讨论
使用Fluent软件,首先明确研究对象性质,建立研究对象的物理模型,并建立研究对象数学模型;然后输入流体流动的初始条件和边界条件进行计算;最后输出所需的图像、曲线或数据等相关结果。本实例的已知模拟条件:均匀直圆管长 L= 3m直径 d=0.1m流体进口速度为 v= 0.01m/s 与 v= 0.1m/s介质为水。由已知条件可知, v= 0.01m/s时管内流体为层流状态, v= 0.1m/s 时,管内流体为紊流状态。通过模拟,得到结果如图1~8所示:

图1 圆管充分发展段层流流体速度分布云图

图2 圆管充分发展段紊流流体速度分布云图

图3 圆管充分发展段层流流体速度等值线图
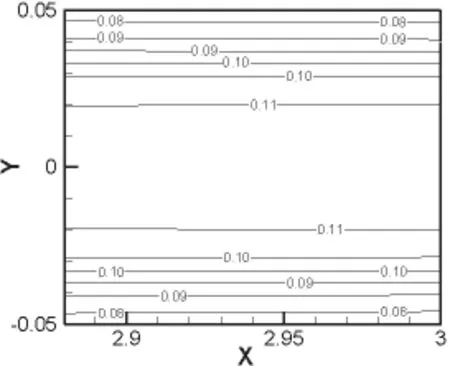
图4 圆管充分发展段紊湍流流体速度等值线图
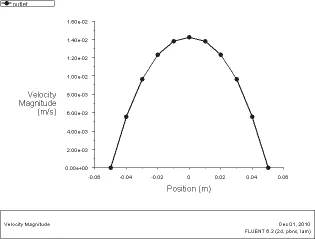
图5 圆管充分发展段过流断面层流流体速度分布曲线

图6 圆管充分发展段过流断面紊流流体速度分布曲线
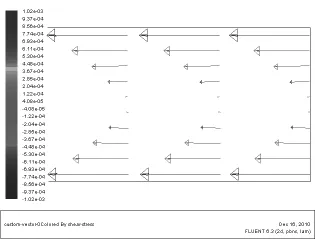
图7 圆管充分发展段层流流体切应力分布
流体流入管内时首先经历入口段,再进入充分发展段。在入口段过流断面速度分布不断发生变化,其长度可利用经验公式算出(在这里主要研究管内充分发展段流体的两种流动状态如图1、图2所示)。从图中可以看出,两种流动状态下,流体的速度均在管壁处为零,管道中心处最大,但其变化规律并不相同,这种区别在图3、图4的速度等值线图中表现得更为明显,层流时管内流体速度从管壁到管中心逐渐增大,而紊流时在管内近壁处,速度梯度较大,并很快接近于管内中心处最大值。图5、图6为两种流动状态下管内充分发展段横断面的速度分布曲线,从图中可以看出,层流时,圆管内横断面速度分布呈抛物线,与式(2)相吻合;紊流时在近壁处,速度近似直线规律变化,与式(4)相吻合;在紊流核心区,速度比较均匀,速度梯度比较小,符合紊流速度的对数分布规律,与式(5)吻合。图7、图8为两种流动状态下管内充分发展段横断面的切应力分布曲线,从图中可以看出其切应力均为在管壁处最大,在管心处为零,并呈K字形分布,但是其大小并不相等,符合两种流态下切应力的变化规律。
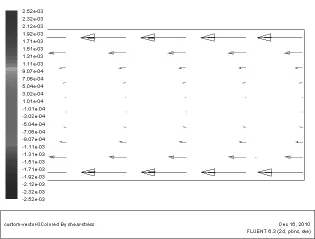
图8 圆管充分发展段紊流流体切应力分布
3 结束语
从上述对定常不可压缩流体在圆管内流动的理论推导和数值模拟可以得出,利用Fluent软件可以将模拟结果以图像、曲线等形式表现出来,定性定量地分析两种流态下管内流体的速度分布及切应力分布等规律,帮助学生理解、消化与记忆。实践表明,在枯燥的理论讲解及公式推导过程中配以Fluent数值模拟,可以调动课堂气氛,增加学生的学习兴趣,提高教学效果。
[1] 郑洁庆,邹峰,张军,等.CFD软件在工程流体力学教学中的应用[J].中国现代教育装备,2007,10:119~121
[2] 李国威,崔俊奎.基于Fluent的流体力学教学课件素材制作研究[J].中国现代教育装备,2009,5:76~77
[3] 刘荣,陶乐任.Fluent数值模拟在制冷与空调领域中的应用[J].低温与超导,2010,10:77~80
[4] 张也影.流体力学[M].北京:高等教育出版社,1999
[5] 赵振南.传热学[M].北京:高等教育出版社,2008
Application research of multimedia teaching about viscosity f uid f owing in tube based on Fluent
Dong Jinling, Li Guowei
Liaoning technical university, Fuxin, 123000, China
2011-01-10 稿件编号:1101032
董金玲,助教。
辽宁工程技术大学应用创新型人才培养立项课题“CFD技术在流体力学多媒体教学中的创新培养研究”(编号:YBQ104021);辽宁工程技术大学“流体力学校级精品课程”(编号:2007-03)

