有限元法中非关联流动条件下刚度矩阵的存储方式及平衡方程求解

魏匡民 苏佩珍

（1.河海大学 水工结构研究所，南京 210098；2.广西壮族自治区 水利电力勘测设计研究院，南宁 530000）

有限元法由于其原理简单，理论严密，解决问题便捷，在岩土工程计算中得到了广泛应用.然而由于岩土材料的复杂性，其本构关系往往采用非关联的流动法则，即屈服面和塑性势面不一致，假定塑性应变方向和塑性势面外法线方向一致，以此确定塑性应变的流动方向，著名的Lade－Duncan模型就采用了非关联的流动法则.对于单屈服面，屈服函数和塑性势函数不一致的情况，弹塑性柔度矩阵一般可以写为［1］

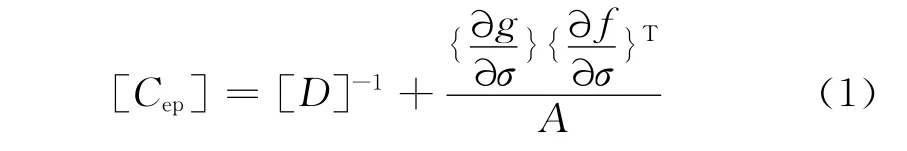
式中，［D］－1为弹性矩阵的逆矩阵；｝为塑性势面外法线方向；为屈服面的外法线方向，A为与屈服面硬化行为相关的参数.可以看出，非关联的流动法则条件下，弹塑性矩阵［Cep］不再是一个对称矩阵.而有限元计算中弹塑性矩阵的不对称也会使得叠加后的整体刚度矩阵的不对称，从而整体劲度矩阵的存储方法和平衡方程的求解也不同于常规方式.

国内研究大多采用对称的弹塑性矩阵、整体刚度矩阵采用一维压缩存储、平衡方程采用LU（Crout分解）分解求解，而对于非关联流动法则下的程序设计涉及甚少.所以，介绍作者设计的非关联流动法则条件下整体刚度矩阵的存储方式以及平衡方程的求解方法，并在文末给出了相关的程序，文中建议的方法只要求在常规有限元程序框架下稍加改动，执行简便.常规有限元法的基本原理和程序设计见文献［2］.

1 非关联流动法则下整体刚度矩阵的存储方法

1.1 单元刚度矩阵和整体刚度矩阵的关系

这里引用文献［2］中的例子来说明单元刚度矩阵和整体刚度矩阵之间的关系，并依据此提出在非对称弹塑性矩阵条件下整体刚度矩阵的压缩存储方法.图1为4单元6结点的简单结构，其单元刚度矩阵和叠加后的整体刚度矩阵对应如图2所示.其中kⅠij为单元刚度矩阵元素，上标表示单元号，下标表示关联的节点号.

图1 单元编号和结点的整体、局部编号

图2 叠加后的整体刚度矩阵

可以看出整体刚度矩阵在元素分布上是对称的，这种对称来源于各结点自由度之间的相互作用关系，两个没有联系的自由度对应的刚度矩阵元素为0，当结构规模增大，自由度数目增多时，无关联的自由度数目也增多，整体刚度矩阵的零元素也随着增多，并且发现整体刚度矩阵非零元素成带状分布.所以，整体刚度矩阵元素的分布规律是由有限元几何模型条件决定的，与材料的本构关系无关.当采用不关联的流动法则时，整体刚度矩阵元素分布位置不会发生变化，且元素位置分布对称.

不同的是，非关联的流动法下，某一单元的单元刚度矩阵可能不对称，单元刚度矩阵叠加到整体刚度矩阵后，整体刚度矩阵对称位置上的元素大小也就可能不再相等.常规的有限元方法中只存储对称矩阵的一半元素，采用非关联流动法则时刚度矩阵中带宽以内（整体刚度矩阵中每行第一个非零元素到最后一个非零元素的元素个数称为带宽）的元素都要存储.所以存储容量是常规方法的两倍.这里将带宽以内的区域称为“存储有效区”，对带宽以外的零元素则不再存储.

1.2 整体刚度矩阵的存取方式

常规方法中整体刚度矩阵采取一维压缩存储的方法，通过设置指示矩阵使得压缩后的一维矩阵元素与整体刚度矩阵半带宽以内元素一一对应，减小存储空间，方便元素存取.通过1.1中的讨论知道弹塑性矩阵不对称时，整体刚度矩阵元素分布依然对称，但是对称位置上元素数值可能不再相等，利用这个规律现在将存储方式改变如下:

（1）采用两个同样大小的一维矩阵CKO（＊）和CKT（＊）分别用来存储整体刚度矩阵的下三角和上三角半带宽以内的元素.

（2）指示矩阵IA1（＊）的形成和常规有限元方法相同.

（3）对每一个单元循环，形成单元刚度矩阵，并根据判断条件叠加到整体刚度矩阵，具体方法如下:①如果单元刚度矩阵某一元素SKE（I，J）满足NN（I）＞NN（J），则将其叠加到整体刚度矩阵的下三角区域，也就是叠加到一维矩阵CKO（IA1（NN（I））－（NN（I）－NN（J）））位置，其中NN（＊）为单元自由度矩阵，用来将单元局部自由度和整体自由度联系起来.②如果单元刚度矩阵某一元素SKE（I，J）满足NN（I）＜NN（J），则将其叠加到整体刚度矩阵的上三角区域，也就是叠加到一维矩阵CKT（IA1（NN（J））－（NN（J）－NN（I）））区域，其中 NN（＊）单元自由度矩阵，用来将单元局部自由度和整体自由度联系起来.③如果单元刚度矩阵某一元素SKE（I，J）满足NN（I）＝NN（J），即其叠加到整体刚度矩阵的对角线上，这里将其叠加到一维矩阵CKT（IA1（NN（J））－（NN（J）－NN（I）））上.同时将 CKO（IA1（NN（J））－（NN（J）－NN（I）））赋值为1.0，这样的做法方便下文的LU分解.

经过了以上3个步骤后，整体刚度矩阵由CKO（＊）和CKT（＊）共同存储，并且共用一个指示矩阵，压缩前的整体刚度矩阵和压缩存储后的一维矩阵的关系为

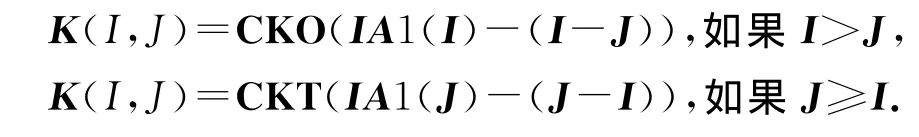
2 平衡方程求解

岩土计算中非线性平衡方程的求解方法有增量法，初应力法，初应变，中点增量法等，但其最基本的方式都是求解线性方程组

式中，［K］为整体刚度矩阵；［R］为等效结点荷载列阵；［δ］为所求的结点位移.

LU分解法由于计算方法简单，易于实现，使用比较普遍.常规有限元方法中，由于整体刚度矩阵的对称性以及刚度矩阵分解前后半带宽不变，根据线性方程回代过程的特点，程序中只存储L矩阵的对角元素和U矩阵的有效元素（半带宽以内），分解后矩阵的元素也可以存储在之前的整体刚度矩阵内，节省了存储空间，具体作法可见文献［2］.当整体刚度矩阵不再对称时，相应的程序设计要进行改变.这里将修改后的方法说明如下.

2.1 刚度矩阵的分解

最基本的LU分解方法如下［3］，［K］为整体刚度矩阵，［L］和［U］分别为下三角阵和上三角阵，小写字母代表相应矩阵中的元素.

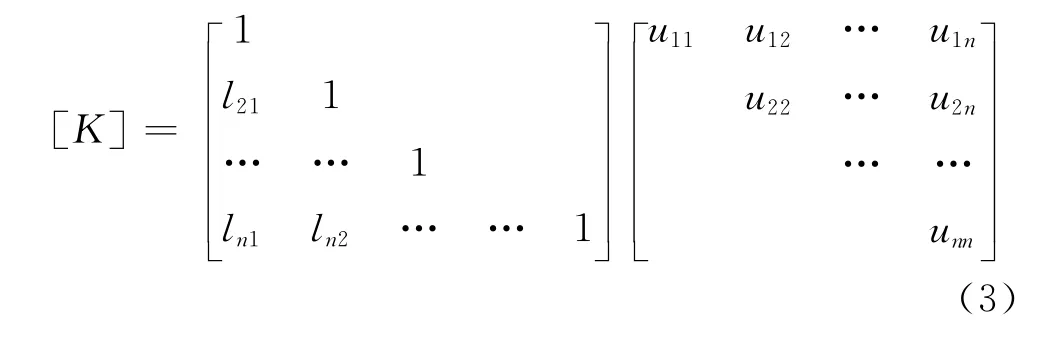
则LU分解步骤包括:

计算U的第r行，L的第r列元素（r＝2，3，…，n），对（2）（3）两个步骤循环.

由步骤（1）～（3）可知，当“A矩阵元素分布对称时，分解后上三角矩阵和下三角阵的带宽和原来一致，即A矩阵中第i行第一个非零元素之前的零元素分解之后仍为0元素，第j列第一个非零元素之前的零元素分解之后仍为0元素，可以利用这个特点将分解后的L，U矩阵存在矩阵K相应的位置上，以节省存储空间.

在执行步骤（1）～（3）的过程中，只存储了刚度矩阵带宽以内的元素，其他部分的元素并没有被存储，而没有被存储的元素均为零元素，所以在执行每一个步骤时都要对元素uij，lij，aij通过指示矩阵进行位置判断，如果此元素位于带宽以内则通过指示矩阵将其从一维压缩矩阵中取出，若不在存储区则值赋为0.以上各步骤中判断方法为:若元素lij，kij位于下三角区域且其所在的列号小于I－［IA1（I）－IA1（I－1）］＋1，则其为零元素.若元素uij，kij位于上三角区域且所在行号小于K－［IA1（J）－IA1（J－1）］＋1，则其为零元素.对于存储区的元素，若处于下三角区域则K［I，J］＝CTO（IA1（I）－（I－J）），若位于上三角区则有K［I，J］＝CKT（IA1（J）－（J－I）），按照此存储方法可对刚度矩阵进行分解.其中IA1（＊）为指示矩阵.

2.2 回代求解

将整体刚度矩阵分解以后得到

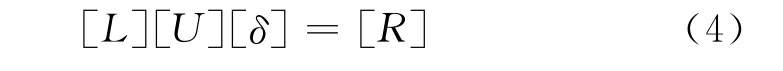
分两个步骤对方程进行求解，即［L］［y］＝［R］，［U］［δ］＝［y］，回代计算过程如下:

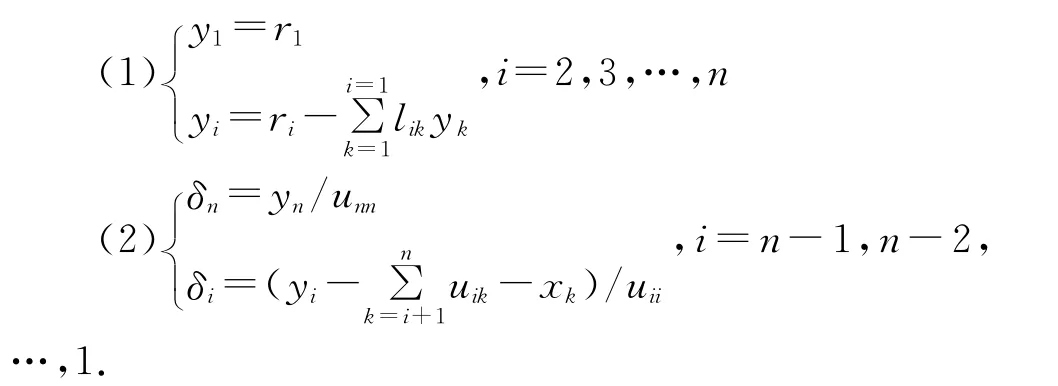
由通过2.1中刚度矩阵的分解，下三角矩阵［L］存储在CKO（＊）中，上三角矩阵［U］存储在CKT（＊）中，在执行步骤（4）（5）时同样要进行判断lij，uij是否位于存储区域以内，判断方法为:若元素lij所在的列小于I＝［IA1（I）－IA1（I－1）］＋1，则其为零元素，否则L（I，J）＝CTO（IA1（I）－（I－J））；若元素uij所在行小于J＝［IA1（J）－IA1（J－1）］＋1，则其为零元素，否则U（I，J）＝CTO（IA1（J）－（J－I））.这样就能求出结点位移.回代程序中［Y］和［δ］都可以存储在矩阵［R］中以节省存储空间.其中IA1（＊）为指示矩阵.

3 程 序

按照1.1和1.2中方法得到不对称的整体刚度矩阵和指示矩阵后，再和等效结点荷载列阵一起按照第2节中所述方法进行平衡方程求解，现将LU分解（DECOMP）和回代求解（FOWBAC）子程序列出供参考（Fortran95语言编写）.子程序中的形参数名称与上文使用的代号一致.

4 算 例

通过一个算例说明本文程序的运行结果.简单地假定非关联流动法则条件下，某整体刚度矩阵｛K｝和荷载列阵｛R｝如式（5），整体刚度矩阵的的特点是带宽以内元素位置对称但数值不一定相等.由式（5）可知自由度数为5，CKO（＊）和CKT（＊）各存储9个元素.

程序执行中对整体刚度矩阵进行了一维压缩存储，按照上述一维压缩存储方式，指示矩阵IA1（5）＝｛1，3，5，8，9｝，下三角元素存储矩阵CKO（9）＝｛1，2，1，3，1，3，4，1，1｝，上三角元素存储矩阵 CKT（9）＝｛4，3，5，2，4，1，1，4，3｝，自由度数 NQ＝5.运行子程序DECOMP后整体刚度矩阵被分解为上三角矩阵和下三角矩阵，仍存储在原来的位置，此时CKO（9）＝｛1.0，0.5，1.0，0.857，1.0，0.857，1.0，1.0，1.0｝，CKT（9）＝｛4.0，3.0，3.5，2.0，2.285，1.0，0.14，3.0，3.0｝.若写成压缩前的二维形式为:

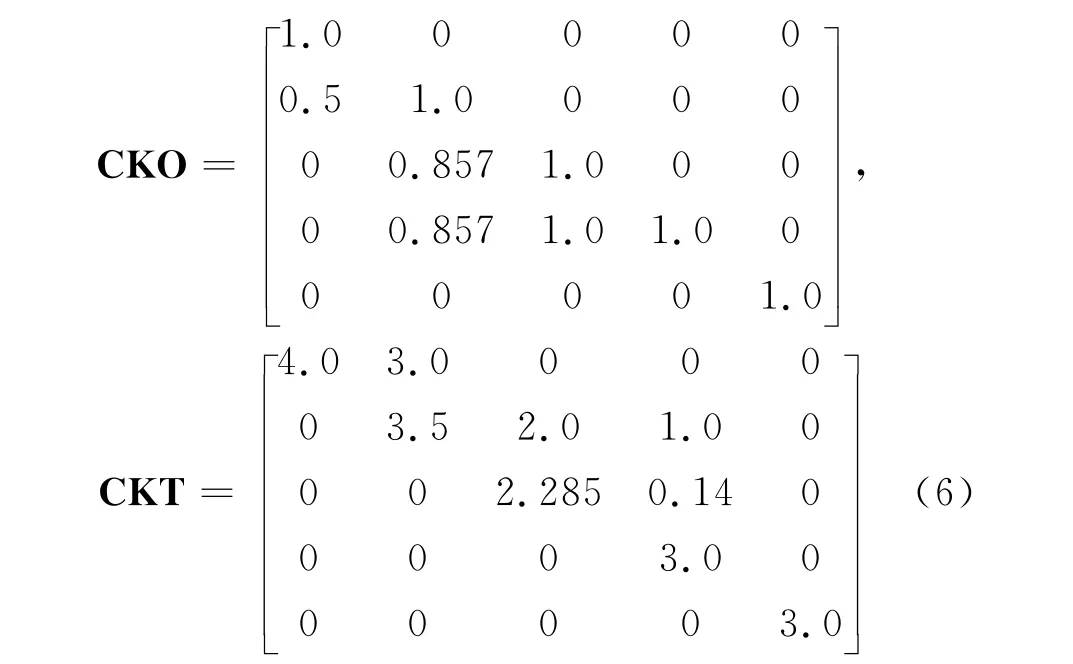
最后，调用子程序FOWBAC回代计算，求得结点位移列阵（5）｛1.0，1.0，1.0，1.0，1.0｝.

5 结 论

本文结合非关联流动法则下整体刚度矩阵存和平衡方程求解规律，给出了有限单元法中非关联流动条件下，整体刚度矩阵的存储规律和平衡方程的求解思路，使用和常规有限元相同的指示矩阵实现了对刚度矩阵的一维压缩存储，在平衡方程求解过程中，通过判断元素是否在“存储有效区”进行刚度矩阵元素的分解和存储.此方法在常规有限元方法程序基础上做较少的改动即可以完成非关联流动本构下的弹塑性有限元分析.

［1］钱家欢，殷宗泽.土工原理与计算［M］.北京:中国水利水电出版社，1996.

［2］陈国荣.有限单元法原理及应用［M］.北京:科学出版社，2009.

［3］李庆扬，王能超，易大义.数值分析［M］.北京:清华大学出版社，2008.