关于 Burger s方程族的解的注记
胡六锋, 张大军
(上海大学理学院,上海 200444)
关于 Burger s方程族的解的注记
胡六锋, 张大军
(上海大学理学院,上海 200444)
讨论等谱与非等谱 Burgers方程族的精确解.两个方程族都可以通过 Cole-Hopf变换化为线性形式,利用Wronskian方法中Wronskian元素的构造技巧给出若干不同形式的精确解,研究这些解之间的关系及动力学特征.
Burgers方程族;精确解;动力学特征
Burgers方程是流体力学中基本的偏微分方程之一,应用于多个领域,如气体动力学模型、湍流模型、交通流模型等[1-2].该方程可通过 Cole-Hopf变换[3-4]线性化,该线性化会直接导致其孤子的特殊碰撞行为:分解或融合 (t→ -t)[5-6].由 Lax的可积性可知,Burgers方程与谱问题 φx=(u+λ)φ或 Levi族[7]密切相关,因此,能导出等谱与非等谱 Burgers方程族[8-9].
本工作主要研究Burgers方程族的解.首先通过Cole-Hopf变换得到方程族的线性形式,然后讨论其精确解,应用文献 [10-11]中构造 Wronskian元素的技巧,给出 Burgers方程族更多的解,并能清楚地分析这些解之间的相互关系.
1 Burger s方程族及其线性化
首先,回顾 Burgers方程族的 Lax可积性.不同于文献[9],本研究考虑下面的线性问题[7-8]:

式中,A和B分别为位势 u和谱参数λ的待定函数.由相容性条件 φxxt=φtxx,得

式中,


式中 ,T=∂+u+ux∂-1=∂(∂+u)∂-1.如果取λt=λn+1,(a0,b0)=(a,x),则由式 (2)可得非等谱方程族为

特别地,当 n=1时,式 (3)给出的 Burgers方程为

而式 (4)给出的非等谱 Burgers方程为

式 (5)和 (6)的 Lax对都可由式 (1)表示.与式 (5)对应的 Lax对中,A=aλ-ux,B=λ+u;与式 (6)对应的 Lax对中 ,A=aλ-xux-u,B=x(λ+u).
等谱与非等谱 Burgers方程均可化为线性方程[9].由 Cole-Hopf变换[3-4]

及式 (3),可得

或
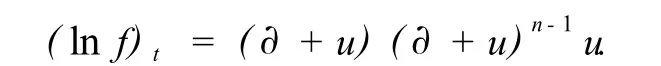
进而,有

式中,
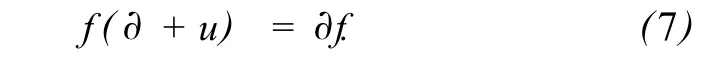
重复利用式 (7),最后得出
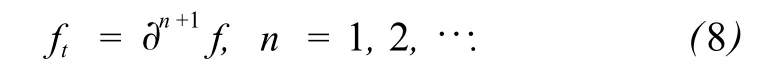
式 (8)为式 (3)的线性化形式,因此,只需讨论式(8).
类似地,非等谱 Burgers方程 (4)的线性形式为

2 Burger s方程族的解
2.1 基本解与一般解
本节讨论 n≥1时 Burgers方程族的解.式 (8)的一个基本解为

式中,kj,为常数.利用Wronskian元素的构造方法[11],可生成式 (8)的其他 2种形式的解,即

且式 (11)和 (12)是线性无关的.
为了方便应用,将式 (8)的 4种基本解列出:

于是,可得等谱 Burgers方程族 (3)的一般解为

式中,a0,aj,aj,s,aj,s,0为任意常数.
类似地,对于非等谱 Burgers方程族 (4)的线性形式 (9),也可得到 4种基本解:

式中,b0,bj,bj,s,bj,s,0,cj,dj均为任意常数.
为了下文分析等谱和非等谱 Burgers方程 (n=1)的动力学特征,在此列出前几个 f1,j,s,f1,j,s,0和g1,j,s,g1,j,s,0的具体表达式.




图 1 等谱 Burger s方程的解Fig.1 Solution for the isospectral Burger s equation



图 2 非等谱 Burgers方程的解Fig.2 SolutionforthenonisospectralBurgersequation
3 结 束 语
本研究借助 Wronskian方法中构造 Wronskian元素的技巧,得到等谱与非等谱 Burgers方程族的一般解,讨论了等谱与非等谱 Burgers方程某些解之间的关系,并进行了动力学分析.
[1] BURGERS JM.The nonlinear diffusion equation[M].Boston:Kluwer Aca,1974.
[2] WHITHAM GB.Linear and nonlinear waves[M].New York:Wiley-Interscience,1974.
[3] HOPF E.The partial differential equation ut+uux=uxx[J].Comm Pure Appl Math,1950,3:201-230.
[4] COLE JD.On a quasilinear parabolic equation occurring in aerodynamics[J].Quart Appl Math,1951,9:225-236.
[5] HIETARINTA J. Scattering of solitons and dromions[M]∥PIKE R,SABATIER P.Scattering:scattering and inverse scattering in pure and applied science.London:Academic Press,2002:1773-1791.
[6] WANG S,TANG X Y,LOU S Y.Soliton fission and fusion: Burgers equation and Sharma-Tasso-Olver equation[J].Chaos Solitons and Fractals,2004,21:231-239.
[7] LEV I D.Nonlinear differential difference equations as Bäcklund transformation[J].J Phys A:Math Gen,1981,14:1083-1098.
[8] 陈登远.孤子引论[M].北京:科学出版社,2006.
[9] LEV ID,RAGNISCO O,BRUSCHI M.Continuous and discrete matrix Burgers’hierarchies [J]. Nuovo Cimento B,1983,74:33-51.
[10] MA W X,YOU Y C.Solving the Korteweg-de Vries equation by its bilinear form:Wronskian solutions[J].Trans Ame Math Soc,2005,357:1753-1778.
[11] ZHANG D J.Notes on solutions in W ronskian form to soliton equations: KdV-type [J/OL]. arXiv:nlin/0603008v3,2006:1-45.[2006-06-28].http:∥www.arxiv.com/abs/nlin/0603008.
[12] Exact solutions to the Burgers equations[EB/OL].[2010-12-11].http:∥eqworld.Tpmnet.ru/en/solutions/npde/npde1301.pdf.
Notes on Solutions to Burger s Equation Hierarchies
HU Liu-feng, ZHANGDa-jun
(College of Sciences,ShanghaiUniversity,Shanghai200444,China)
We consider exact solutionsfor the isospectral and nonisospectral Burgershierarchies.The two hierarchies can be linearized through the Cole-Hopf transformation. Solutions are given using the technique for selecting Wronskian entries.Relationship between some solutions and their dynamic characteristics are investigated.
Burgers equation hierarchies;exact solutions;dynamic characteristics
O 175
A
1007-2861(2011)01-0094-06
10.3969/j.issn.1007-2861.2011.01.016
2009-09-18
国家自然科学基金资助项目(11071157);上海市教委重点学科建设资助项目(J50101)
张大军 (1971~),男,教授,博士生导师,博士,研究方向为孤立子理论与可积系统.E-mail:djzhang@staff.shu.edu.cn
(编辑:孟庆勋)

