种植密度对基因芯片表面应力的影响
李晶晶, 谭邹卿, 秦 巍
(1.上海大学上海市应用数学和力学研究所,上海 200072;2.上海大学理学院,上海 200444;3.上海大学 期刊社,上海 200444)
种植密度对基因芯片表面应力的影响
李晶晶1,2, 谭邹卿1, 秦 巍3
(1.上海大学上海市应用数学和力学研究所,上海 200072;2.上海大学理学院,上海 200444;3.上海大学 期刊社,上海 200444)
利用能量法分析无标记生物检测中基因芯片的纳米力学行为.首先,考虑微悬臂梁机械能、基因层静电能、水合能和构型熵,建立基因芯片能量模型;其次,利用能量最小原理,得到芯片稳态弯曲的曲率半径与表面应力之间的关系;最后,预测种植密度对芯片表面应力的影响,同时将预测结果与有关实验数据进行比较,证明该方法的可靠性.
基因芯片;生物能;纳米力学;种植密度;表面应力
本工作考虑双链 DNA的静电能、水合能、构型熵和层合梁的机械能,借助 Strey由实验得到的双链DNA自由能的经验势和层合梁两变量方法[1],建立了DNA芯片的总能量模型.同时,利用能量最小原理计算基因芯片的表面应力响应,数值分析了种植密度对基因芯片表面应力的影响.最后,将预测结果与有关实验数据进行比较.
1 数学模型
基因芯片一般由层合微悬臂梁和吸附在微悬臂梁上的 DNA分子生物层组成,如图 1所示.现以微悬臂梁形心轴为 x轴,沿悬臂梁的厚度方向向下为y轴,建立坐标系.设悬臂梁的长、宽、高分别为 l,b1,h,氮化硅 (SiNx)层、金 (Au)层和铬 (Cr)层的厚度分别为 hSiNx,hAu,hCr,各层相应的弹性模量分别为ESiNx,EAu,ECr.
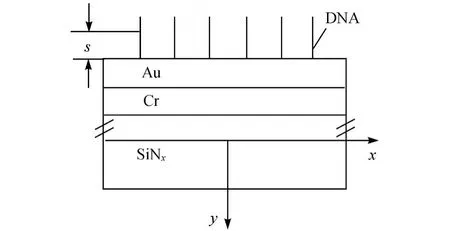
图 1 DNA芯片的简化模型Fig.1 Sim plif ied model of DNA ch ip
基因芯片系统的总能量 F可分为非生物层的机械能 FM和DNA分子的生物能 FB[1,5],即

DNA分子的生物能 FB通常又可分为静电能、水合能和构型熵[5].Strey等[6-7]采用溶致液晶理论模拟了 dsDNA生物层,在盐溶液中建立了 dsDNA生物层能量模型.基于 Strey液晶体 DNA的状态方程[6-7],由半柔性的聚合 dsDNA的静电作用和水合作用而产生的单位长度的生物能为
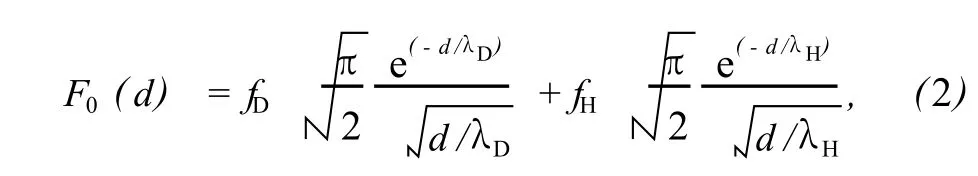
式中,λD为 Debye屏蔽距离,λH为水的关联长度,fD和 fH为经验常数.
考虑到生物大分子构型熵,根据有序聚合物的分析,dsDNA单位长度的生物能 F1(d)可表示为如下关于 dsDNA链间距离 d的函数形式[5-7]:
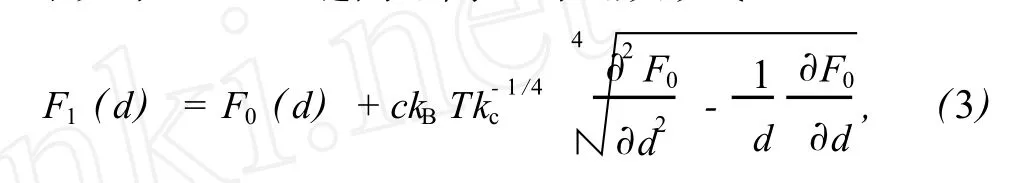
式中,c为无量纲常数,kB为 Boltzmann常数,T为温度,kc为 dsDNA的弯曲强度 (kc=kBTlp,lp为 dsDNA的持续长度).
采用层合梁的两变量模型[8-12]描述基因芯片的几何变形,以ε0表示形心轴正应变,R表示中性轴曲率半径,则距离形心轴为 y处的轴向正应变为
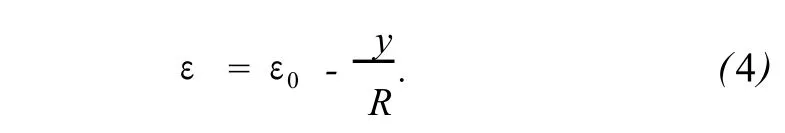
在生物层变形前后,DNA保持直链构形,其统计长度为 Lc~Na,其中 N为 dsDNA的碱基对数,a为碱基对之间的距离.若基因芯片表面处理 dsDNA链间距离为 d0,检测后距离金层表面 s处的 dsDNA链间距离为 d(s),则由式 (4)可得
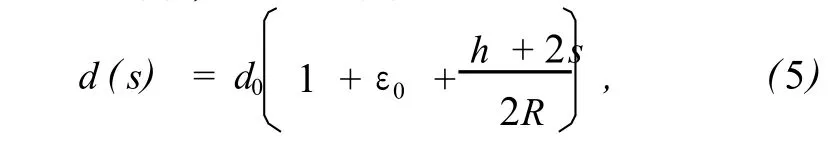
式中,d0=1/η,η为 DNA的种植密度.将式 (5)代入式 (3),并在生物层内积分,可得系统的生物能为

显然,由式 (6)无法直接积分得到生物能 FB的表达式.
芯片的机械能为
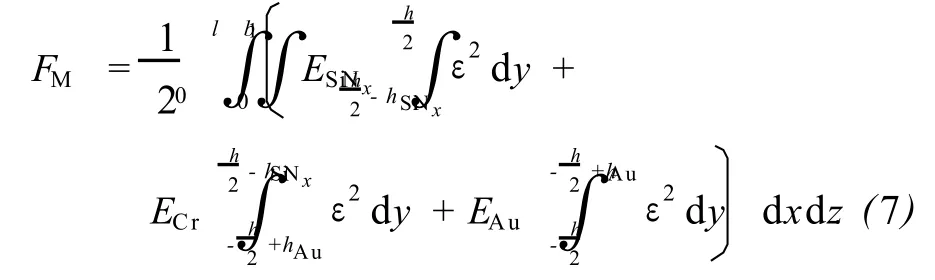
将式 (4)代入式 (7)并积分,得
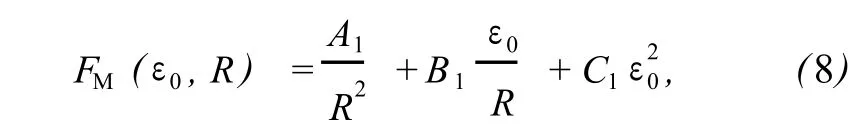
式中,
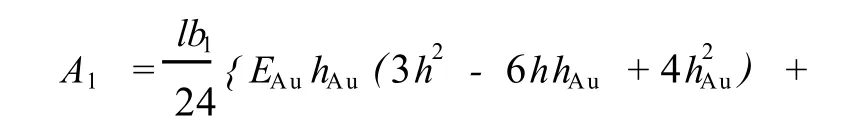

将式 (6)和 (8)代入式 (1),可得芯片系统关于两变量ε0和 R的总能量为 F=F(ε0,R).根据能量最小原理,利用 Mathemaica软件数值求解,可获得dsDNA芯片系统达到稳态时的曲率半径 R和形心轴正应变ε0.
进一步,考虑到氮化硅层的厚度远大于金层和铬层,利用简化的单层梁的 Stoney公式[13],可得到微悬臂梁表面应力和曲率半径 R之间的关系为
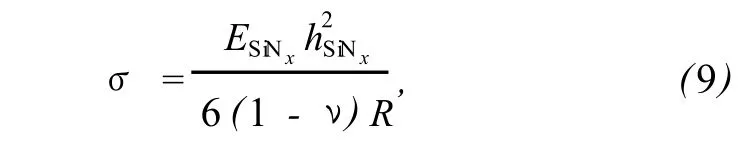
式中,ESiNx和ν分别为悬臂梁材料 SiNx的弹性模量和泊松比.
2 数值算例及讨论
根据 Stachowiak等[4,6-7]提供的实验参数,当缓冲液浓度分别为 0.1和 1.0 mol/L时,生物层经验参数分别取 f0=4.1×10-10J/m,b=1.1×10-7J/m,c=0.8,λD=0.974 nm,λH=0.288 nm和 f0=0,b=1.7 ×10-7J/m,c=1.2,λD=0.308 nm,λH=0.290 nm;芯片其他参数取值为 hSiNx=0.5μm,hAu=25 nm,hCr=5 nm,h=hSiNx+hAu+hCr,l=200μm,b1=40μm;ESiNx=85 GPa,EAu=73 GPa,ECr=108 GPa;a=0.34 nm,N=10 nt,T=298 K,kB=1.38 ×10-23J/k,lp=50 nm,ν=0.25.
图 2(a)和图 2(b)分别为缓冲液浓度为 0.1和1.0 mol/L时,种植密度对微悬臂梁表面应力的影响.与实验数据进行比较,可以看到,芯片的表面应力随着种植密度的增大而逐渐增加.数值预测结果与实验数据吻合良好,说明了本研究能量模型数值方法的可靠性.
3 结 束 语
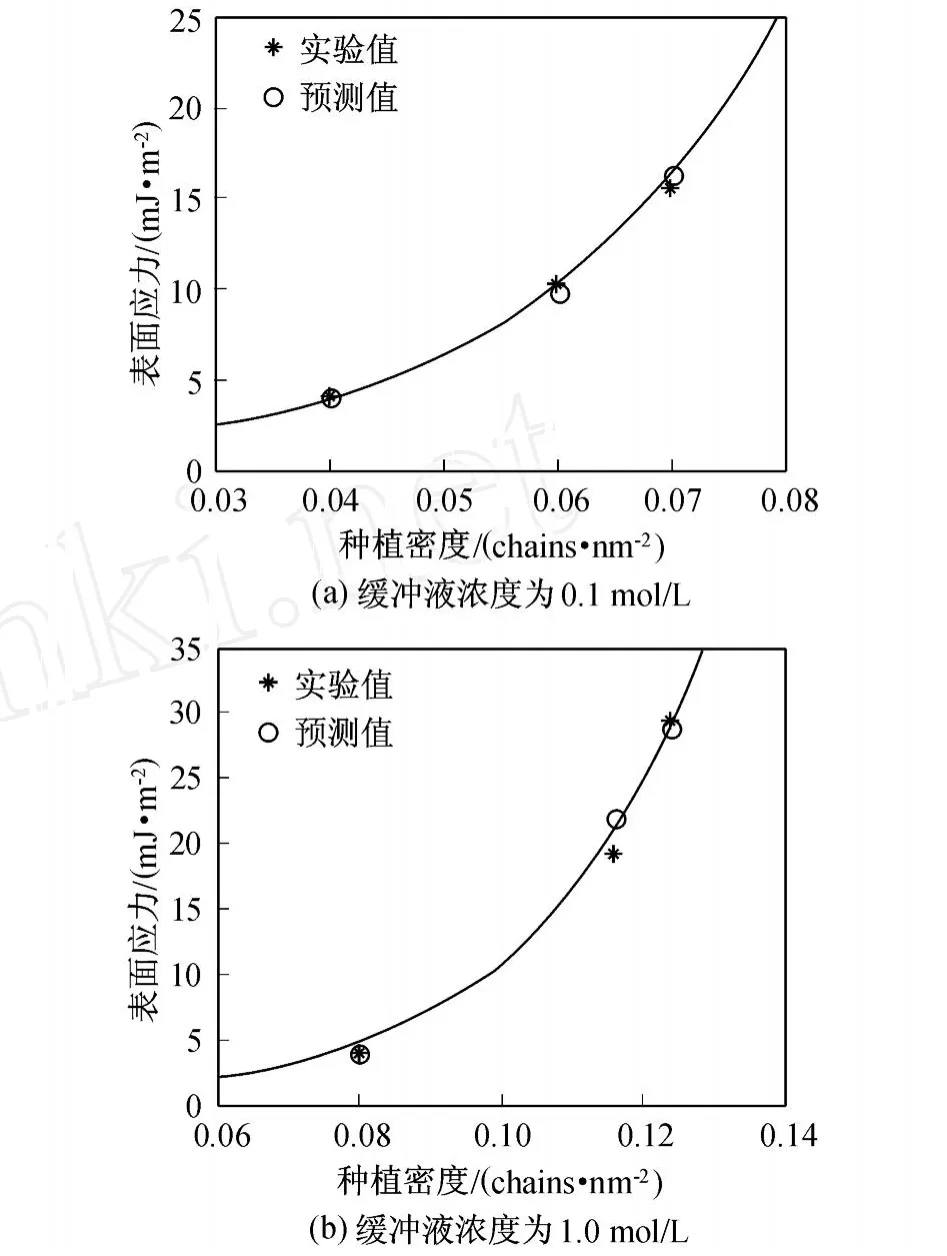
图 2 种植密度对表面应力的影响Fig.2 Influence of pack ing den sities on surface stress
本工作给出了连续介质力学意义下的芯片曲率半径、表面应力与DNA纳观特征、缓冲盐溶液浓度、芯片宏观机械性质与芯片总能量之间的关系,利用能量最小原理数值预测了基因芯片的表面应力响应.结果表明,当 DNA杂交时,芯片表面应力强烈地依赖于种植密度.该结论与有关实验结果相吻合.
[1] ZHANG N H,SHAN J Y.An energy model for nanomechanical deflection of cantilever-DNA chip[J].JMech Phys Solids,2008,56:2328-2337.
[2] FRITZ J,BALLER M K,LANG H P,et al.Translating biomolecular recognition into nanomechanics [J].Science,2000,288:316-318.
[3] MCKENDRY R,ZHANG J,ARNTZ Y,et al.Multip le label-free biodetection and quantitative DNA-binding assayson a nanomechanical cantilever array[J].PNAS USA,2002,99:9783-9788.
[4] STACHOW IAK J C,YUE M,CASTEL INO K,et al.Chemomechanics of surface stresses induced by DNA hybridization[J].Langmuir,2006,22:263-268.
[5] HAGAN M F,MAJUMDAR A,CHAKRABORTY A K.Nanomechanical forces generated by surface grafted DNA[J].J Phys Chem B,2002,106:10163-10173.
[6] STREY H H,PARSEGIAN V A,PODGORNIK R.Equation of state for DNA liquid crystals:fluctuation enhanced electrostatic double layer repulsion[J].Phys Rev L,1997,78:895-898.
[7] STREY H H,PARSEGIAN V A,PODGORNIK R.Equation of state for polymer liquid crystals:theory and experiment[J].Phys Rev E,1999,59:999-1008.
[8] ZHANG N H. Thermoelastic stresses in multilayered beams[J].Thin Solid Films,2007,515:8402-8406.
[9] ZHANG N H,SHAN J Y,XING J J.An alternative model for elastic bending deformation of multilayered beams[J].JAppl Phys,2006,100:103519.
[10] ZHANG N H,CHEN J Z.An alternative two-variable model for bending problems of multilayered beams[J].ASME JAppl Mech,2008,75:044503.
[11] ZHANG N H,CHEN J Z.Elastic bending analysis of bilayered beams by an alternative two-variable method[J].European Journal of Mechanics A:Solids,2009,28:284-288.
[12] 张能辉,单金英.基因芯片纳米力学行为的能量模型[J].力学季刊,2007,28:54-57.
[13] M IYATAN I T,FUJIHIRA M.Calibration of surface stress measurementswith atomic forcemicroscopy[J].JAppl Phys,1997,81:7099-7115.
Influence of Pack ing Den sities on Surface Stress of Gene Chip
L IJing-jing1,2, TAN Zou-qing1, QIN Wei3
(1.Shanghai Institute of App lied Mathematics and Mechanics,Shanghai University,Shanghai200072,China;2.College of Sciences,ShanghaiUniversity,Shanghai200444,China;3.Periodicals Agency,ShanghaiUniversity,Shanghai200444,China)
Nanomechanical behavior of gene chip in label-free biodetection is studied using the energy method.Considering electrostatic energy,hydration energy and configuration fluctuationsof DNA layer as well asmechanical energy of chip,an energy formula is set up.The relation between curvature radiusof the neutral axis and surface stressof gene chip isobtained according to theminimum p rincip le of energy.Influence of packing densities on surface stress of gene chip is predicted.Theoretical predictions for surface stressof gene chip are compared w ith experimental data to validate the p resented solutions.
gene chip;bioenergy;nanomechanics;packing density;surface stress
Q 66
A
1007-2861(2011)01-0100-03
10.3969/j.issn.1007-2861.2011.01.017
2009-08-12
国家自然科学基金资助项目(0872121);上海市自然科学基金资助项目 (07ZR14037);Multiscale Material Mechanics Fellowship;上海大学系统生物研究基金资助项目;国家杰出青年基金资助项目(10725209);上海市重点学科建设资助项目 (S30106)
李晶晶 (1963~),女,副教授,博士,研究方向为粘弹性理论及其应用、非线性动力学、纳米力学.E-mail:jjli@shu.edu.cn
(编辑:孟庆勋)
由于具有成本低、速度快、灵敏度高等优点,基于微悬臂梁光学挠度方法的无标记生物检测技术得到了迅速发展和广泛关注[1-5].目前,大部分工作是基于一定条件的定性研究实验[2-4].实验表明,单链DNA分子在微梁金层表面的吸附以及单链 DNA分子的杂交所产生的微梁表面应力的变化,可以引起微梁的纳米级弯曲,而且实测挠度与种植密度、分子链长、盐溶液浓度、杂交率、时间、温度、缓冲液流场特性等诸多因素有关.然而,实验结果的分散性和芯片弯曲机理的悬而未决阻碍了这一技术的市场应用前景,仅有少量研究致力于基因芯片的纳米力学行为的定量研究.Hagan等[5]认为生物层的静电能、水合能和构型熵是引起芯片下弯的主要原因.张能辉等借助液晶体 DNA状态方程[6-7]和层合梁两变量模型,建立了 DNA-微悬臂梁系统的新能量模型[1,8-12],利用能量最小原理数值研究了链间距和弹性模量随机性对芯片纳米挠度的影响.

