基于多小波的彩色图像分层树集合分裂算法

陈俊丽, 卿定湖, 李 翔, 万旺根

(上海大学通信与信息工程学院,上海 200072)

基于多小波的彩色图像分层树集合分裂算法

陈俊丽, 卿定湖, 李 翔, 万旺根

(上海大学通信与信息工程学院,上海 200072)

提出一种基于多小波变换的改进的彩色图像分层树集合分裂 (set partitioning in hierarchical trees,SPIHT)算法,将彩色 RGB图像转换到 YCbCr色彩域,Y通道分配到 2倍于 Cb,Cr的比特,在各色彩通道间构造新的方向树结构,重组图像多小波分解系数,进行嵌入式多小波彩色图像 SPIHT编码.结果表明,该算法具有良好的编码效果,性能优于 9/7单小波编码.

多小波;分层树集合分裂;嵌入式编码;空间方向树;图像压缩

本研究利用彩色图像各分量之间的相关性,在SPIHT算法的空间方向树结构基础上引入新的空间方向树结构,并结合图像多小波变换后系数分布的特点,提出改进的多小波彩色图像 SPIHT算法,提高了多小波彩色图像的编码效率.

1 图像的多小波变换

1.1 多小波理论

多小波 (multiwavelet)是指由 2个或 2个以上函数作为尺度函数生成的小波.与单小波相比,多小波同时具有对称性、短支撑性、正交性以及高阶消失矩等良好特性,因此,多小波在信号和图像处理方面具有明显优势.

设向量函数 Φ (t)=(φ1(t),φ2(t),…,φr(t))T,φi∈L2(R),i=1,2, …,r.对 j∈Z,定义L2(R)空间中的闭子空间 Vj={2j/2φi(2jt-k):1≤i≤r,k∈Z}.若空间序列 Vj满足下列条件:

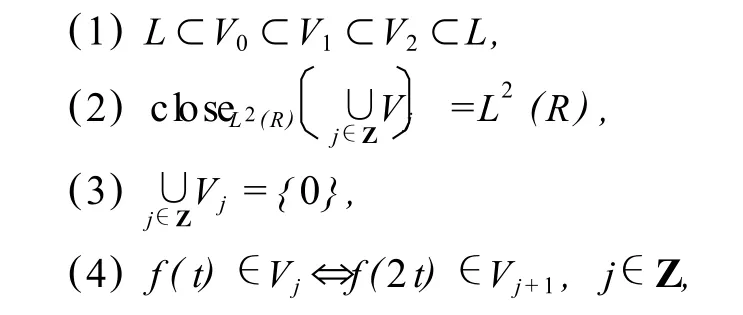
(5){φi(2jt-k):1≤i≤r,k∈Z}为 V0空间的Riesz基,则函数Φ生成 L2(R)空间的多分辨分析(multi-resolution analysis,MRA),且称Φ为 r重多尺度函数.若 {φi(2jt-k):1≤i≤r,k∈Z}为 V0的正交基,则称 {Vj}为正交 MRA.对正交 MRA,定义Vj+1=Vj⊕ Wj,即 Wj为 Vj在 Vj+1中的正交补.若存在ψ1,ψ2,…,ψr,使得其整数平移构成 W0的正交基 ,则Ψ (t)=(ψ1(t),ψ2(t),…,ψr(t))T为 r重正交多小波,且Φ(t),Ψ(t)满足如下双尺度方程:

式中,hk,gk都为 r×r阶的滤波器矩阵.

将单小波中分解与重构的Mallat算法推广至多小波,可以得到如下多小波的分解与重构算法:

式中,Cj,k= (c1,j,k,c2,j,k,…,cr,j,k)T,Dj,k= (d1,j,k,d2,j,k,…,dr,j,k)T,j,k∈Z,,为 hm,gm的共轭转置.与单小波不同,在多小波情况下进入Mallat算法的初始尺度系数为矢量,因此,必须先对信号进行预处理.相应地,重构时还需进行后滤波.

1.2 图像多小波系数的重组策略

对图像进行多小波变换时,应先对图像的行和列进行前置滤波,并按一定的规则将前置滤波图像的行和列组成向量信号,再进行多小波变换.由于有多个 (r)尺度 (小波)函数的存在,在多小波变换后有 r2个子块.若分解级数为 L,则 L级多小波变换将图像分解为 r2(3L+1)个子块,如图 1所示.

基于小波变换的图像压缩算法中,EZW算法和SPIHT算法较好地利用了不同子带间小波系数的相似性,使得输出的比特流具有嵌入式特性,但这 2种方法均是针对单小波变换.由于经过多小波变换后,产生了不同于单小波变换的子带结构,破坏了上述算法所假设的零树结构,因此,需要根据图像多小波变换的特点,对多小波系数进行重新排列,以达到SPIHT编码要求 (见图 2).

对于 GHM多小波来说,分解后的每个子带的2×2个子块间存在大量相关性.为了保持这种相关性,将每个 2×2子块的系数进行重组,将对应于同一空间位置的系数放在一起,形成 4个子带LL,LH,HL和 HH.图 2(b)为经过系数重组后生成新的子带.

对于 CL和 SA4多小波,由于多尺度函数的第 2个分量是反对称的,相应的滤波器组的第 2个通道是带通的,所以子块 L0L1,L1L0和 L1L1具有带通性,而L0L0子块具有低通性,存在不相似谱行为,不需要进行系数重组.因此,对于CL和SA 4多小波 ,只考虑对每个高频子带的 2×2个子块系数进行重组,生成 LH,HL,HH子带.图 2(c)给出了 SA 4多小波分解及系数重组后的子带结构.经过系数重组后,不仅达到 SPIHT编码要求,而且充分利用了某个方向子带之间的相关性,得到了更高的压缩效率.

图 1 基于多小波变换的图像分解Fig.1 Image decomposition based on multiwavelet transform

图 2 多小波系数重组方法Fig.2 Rearrangement of multiwavelet transform coeff icients

2 多小波彩色图像 SPIHT算法

2.1 SPIHT算法

SPIHT算法是一种改进的 EZW编码方法,该算法将系数组织在以下 3个集合表中:L IP(不重要系数表)、L IS(不重要集合表)和 LSP(重要系数表).简单的彩色图像压缩编码方法是将彩色图像的YCbCr 3个色彩通道分离,各自独立地进行编码传输.3个色彩平面就有 3个空间方向树 (spatial orientation tree,SOT)结构和 3组 L IP,L IS和 LSP集合.编码后的码流不具备嵌入式特性,因此,必须等待 3个分量的码流全部到达解码端才能进行解码操作,然后恢复图像.而本算法依照 SPIHT的定义,使每一个色彩平面形成各自的 SOT、初始化时,L IP和L IS的值来自于 3个 SOT的根节点,随着 SPIHT算法的执行,比特流在 3个色彩通道之间自动分配,从而解决了码率的不可嵌入式问题,因此,可称该算法为 D_SPIHT算法.

彩色图像转换到 YCbCr色彩域后,同一个像素点的 Y值通常要比 Cb,Cr值大很多,即亮度通道的小波变换系数通常大于 2个色度通道.因此,对彩色图像高比特平面 (编码的系数来自亮度通道)编码时,抑制色度通道中不必要的比特输出,可以有效地提高编码效率.

2.2 改进空间方向树结构的彩色图像 SPIHT算法

对于自然图像,当色度分量存在较大系数时,相应位置的亮度分量也存在相对较大的系数.彩色嵌入式零树小波 (color embedded zerotree wavelet,CEZW)算法的零树结构充分利用了 YCbCr分量之间的相关性 (见图 3(a)),每一个亮度 Y节点不但在本通道内有子节点,在其他 2个色度通道内也有子节点.亮度通道小波系数的模值通常要比色度通道的模值大很多,因此,在初始阶段,编码的显著性系数大多来自于亮度通道.用 wY,wCb和 wCr分别表示 Y,Cb和 Cr通道的小波系数模极大值,并设:

显然,有M ＞N.在 L IP列表中色度分量至少要经过M-N次排序,重要系数则放入 LSP列表中.如果图像尺寸较大,则初始化时大量 Cr,Cb通道的小波系数置于 L IP和 L IS列表内,编码时将会产生过多无效的 0比特,浪费了资源,降低了编码效率.为了更有效地利用 Y,Cb,Cr分量之间的相关性,提高编码效率,本研究提出了一种彩色图像 SPIHT(colour-SPIHT,CSPIHT)零树结构,通道节点间的父子关系如图 3(b)所示.

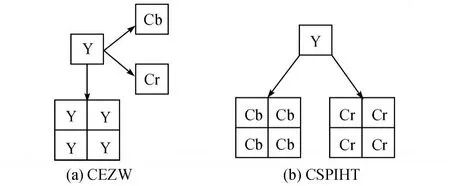
图 3 节点间的父子关系Fig.3 Parent-children node relation

在 CSPIHT零树结构中,对于低频子带中没有子孙节点的 Y分量节点,存在色度分量 Cb,Cr低频子带中相应位置的 4个子节点,通道间和通道内的空间方向树结构如图 4所示.在初始化 L IS和 L IP列表时,仅仅将 Y分量的低频子带节点添加到 L IS和L IP中.当L IS表中的Y通道父节点被扫描到是重要系数时,该色度分量节点才被添加到列表中进行处理.这样就避免了将大量的色度分量添加到L IP和 L IS列表中,节约了资源.

图 4 CSPIHT中空间方向树结构Fig.4 Spatial or ientation tree structure in d ifferent spectral p lanes in the CSPIHT schem e

3 仿真结果及分析

实验性能用峰值信噪比 (peak signal to noise ratio,PSNR)来衡量.设原始图像 x的大小为 M ×N,重构后的图像为 x^,则峰值信噪比定义为

表1 测试平台Table 1 Test platform

本研究选用 24 bit RGB 512×512 Lena和 512×512 Baboon作为测试图像,因为它们分别表示低频含量较高的图像与高频含量较高的图像.在多小波分解前,先将图像转换到 YCbCr色彩域,编码比特率为 0.1比特 /像素 (压缩率 240∶1).分别用双正交 9/7单小波,GHM,CL和 SA 4多小波对图像进行4层和 5层分解,并进行多小波分解系数重组.表2为各图像的 PSNR性能比较.

从表2可知,对于 Lena图像,当分解层次为 4层时,即 LL子带尺寸相对较大时,采用双正交 9/7单小波和 GHM多小波 CSPIHT算法的压缩结果要优于 D_SPIHT算法;当采用 CL和 SA 4多小波时,重建图像的 PSNR大大提高;当分解层次为 5层时,用9/7单小波处理的效果明显改善,略超过 CL多小波,但是仍然略逊于 SA4多小波的处理效果.研究结果表明,多小波彩色Lena图像的压缩性能已经接近双正交 9/7单小波.

对于Baboon图像,由于其包含大量的高频内容,因而较难压缩.即使在低压缩比下,重构的图像中也会出现许多瑕疵.实验结果表明,GHM多小波的压缩性能已经接近双正交 9/7单小波,CL和 SA 4多小波超过了双正交 9/7单小波.但是,不管分解 4层还是 5层,CSPIHT算法的性能都要优于 D_SPIHT算法.

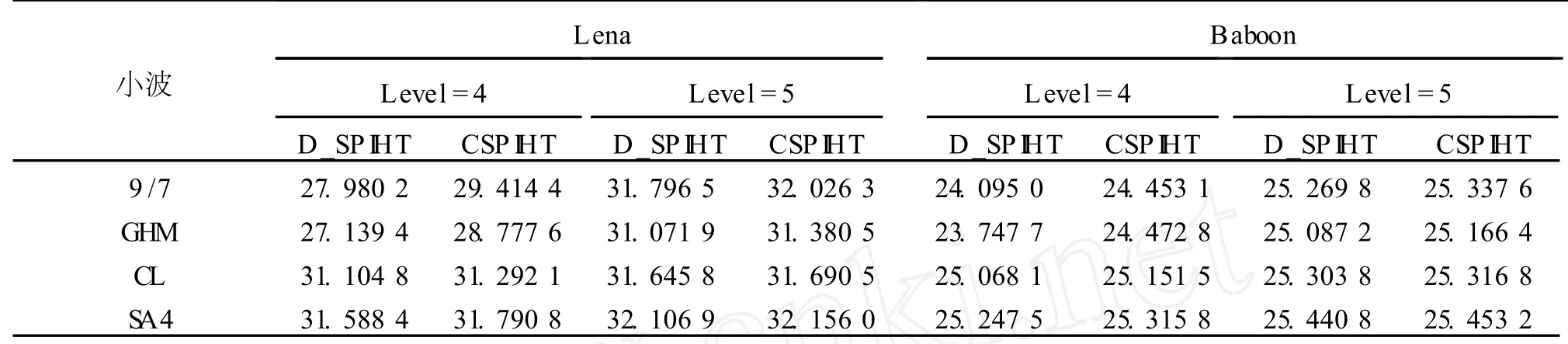
表2 彩色图像压缩算法的 PSNR性能比较Table 2 PSNR compar isons of color images SPIHT based on wavelet and multiwavelet dB

4 结 束 语

本研究利用图像多小波变换后各个子块之间的相关性,重排系数,保持了多小波系数的零树特征.针对彩色图像各分量之间的关系,引入了新的空间方向树结构,提出了改进多小波彩色图像 SPIHT算法.仿真结果表明,在相同压缩比的情况下,改进的CSPIHT算法可以获得更高的峰值信噪比.

[1] ATES H F,ORCHARD M T.Spherical coding algorithm for wavelet image compression[J]. IEEE Transactions on Image Processing,2009,18(5):1015-1024.

[2] DONGW S,SH I GM,XU J Z.Adap tive nonseparable interpolation for image compression with directional wavelet transform[J].IEEE Signal Processing Letters,2008,15:233-236.

[3] PAN H,SIU W C,LAW N F.Lossless image compression using binary wavelet transform [J]. IET Image Processing,2007,1(4):353-362.

[4] ADAM IN,SIGNORONIA,LEONARDIR.State-of-the-art and trends in scalable video compression with waveletbased app roaches[J]. IEEE Transactions on Circuits and Systems for Video Technology,2007,17(9):1238-1255.

[5] SHAPRIO JM.Embedded image coding using zerotree of wavelet coefficients[J]. IEEE Transactions on Signal Processing,1993,41(12):3445-3462.

[6] SA ID A,PEARLMAN W.A new fast and efficient image codec based on setpartitioning in hierarchical trees[J].IEEE Transactions on Circuits and Systems for Video Technology,1996,6(3):243-249.

[7] KHAN M A,KHAN E.Error resilient technique for SPIHT coded color images [C]∥ International Multimedia, Signal Processing and Communication Technologies.2009:237-240.

[8] CHEW L W,ANG L M,SENG K P.Low memory stripbased image compression for color images[C]∥International Conference on Intelligent Human-Machine Systems and Cybernetics.2009:363-366.

[9] CHIEN J C,L ICC.3D multiwaveletpacketson low bitrate color video compression [C]∥ International Conference on Wavelet Analysis and Pattern Recognition.2007:280-285.

[10] WANG A L,L IU P G,CHEN Y S.Multiwavelet-based region of interest image coding[C]∥ International Congresson Image and Signal Processing.2009:1-4.

Set Par tition ing in Hierarchical Trees Algor ithm for Color Images Based on M ultiwavelet

CHEN Jun-li, QINGDing-hu, L IXiang, WAN Wang-gen
(School of Communication and Information Engineering,ShanghaiUniversity,Shanghai200072,China)

We proposes an improved color set partitioning in hierarchical trees(SPIHT)algorithm based on multiwavelet.The algorithm convertsa RGB color image into the YCbCr format.Clearly,bitsassigned to luminance Y p lane are twice than that Cb and Cr chrominance p lanes.A new spatial orientation tree structure is developed between channel p lanes based on SPIHT coding.We embed multiwavelet SPIHT codes for color imageswith the re-combined multiwavelet coefficients.The results show that performance of the proposed codingmethod is superior to SPIHT on 9/7 wavelet.

multiwavelet;set partitioning in hierarchical trees(SPIHT);embedded coding;spatial orientation tree;image compression

O 174.2

A

1007-2861(2011)01-0039-05

10.3969/j.issn.1007-2861.2011.01.006

2010-04-02

国家高技术研究发展计划(863计划)资助项目(2007AA01Z319);上海市教委重点学科建设资助项目 (J50104)

陈俊丽 (1972～),女,副教授,博士,研究方向为小波和多媒体信息处理.E-mail:jlchen@staff.shu.edu.cn

(编辑:赵 宇 )

在数字图像和视频图像编码领域,小波变换具有时频局部性、正交性等特性,与基于离散余弦变换(discrete cosin transform,DCT)的编码技术相比较,可获得更高的信噪比 (压缩率相同时)或压缩率 (信噪比相同时),因而得到广泛的关注,并已应用于MPEG-4和 JPEG2000图像压缩国际标准[1-4].

1993年,Shaprio[5]提出了嵌入式零树小波(embedded zerotree wavelet,EZW)编码方法,取得了良好的图像压缩效果.1996年,Said等[6]基于EZW的基本思想,提出了分层树集合分裂 (set partitioning in hierarchical trees,SPIHT)算法.该算法采用空间方向树表示小波系数的零树结构,提高了编码效率.对于彩色图像,一般采用直接对 3个彩色分量分别进行零树编码的方法.虽然 SPIHT算法直观简单,但是并没有充分利用彩色图像各分量之间的相关性,降低了编码效率.文献 [7-8]从降低误差和减少计算量的角度对彩色图像的 SPIHT编码算法进行了详细分析.在图像处理过程中,正交性能够实现图像的精确重构.然而在实数域中,同时具有紧支、对称、正交的非平凡单小波是不存在的,而多小波由于同时具有正交性、紧支撑性、对称性和高的逼近阶等特性,越来越受到人们的重视[9-10].