制导弹箭捷联惯组在架标定方案研究*
游金川,秦永元,杨鹏翔,严恭敏
(西北工业大学自动化学院,西安 710129)
随着惯性器件技术的日渐成熟和成本的降低,常规无控或简控弹箭纷纷通过加装战术级精度激光或光纤陀螺捷联惯导系统(SINS)进行制导化改造[1-2]。在工程实践中,长时间整弹存储的制导弹箭,由于诸多因素的影响,其捷联惯组(SIMU)的模型参数相对先前实验室标定值将产生较大的变化,使系统无法满足对准和导航精度要求。目前,通常的解决方法是,定期(如一年)将SIMU从弹上拆卸下来,利用精密转台重新标定。这种标定方法虽然能保证高的标定精度,但工作量大,成本高,给系统维护带来很多麻烦。
为了实现弹载SIMU的免拆卸标定,Pittman D N等[3-4]设计了一种对 SIMU添加双轴环架的方案。导弹发射前,利用双轴环架对SIMU进行固定角度的转位(三次双位置转动,第二位置相对第一位置经历两次正交旋转),然后从SINS静态导航位置误差中估计出对准失准角和器件漂移,从而实现SIMU的自标定。而 Gilmore Jerold P 等[5-6]利用三个双自由度动调陀螺仪构成冗余惯导系统,通过周期性的依次反转三个动调陀螺的永磁电机角动量矢量的方向,实现对飞轮的反向控制。这相当于不需要机械环架实现对陀螺的180度转位,从而实现对冗余陀螺的实时标定,而且不影响整套系统的正常导航,但该方案并不适合单自由度光学陀螺构造的惯导系统。文献[7]提出对激光陀螺SIMU进行水平转位,实现双位置对准和元件误差自标定,但该方案仍需要将SIMU从弹上拆除,且没有考虑器件中刻度系数误差的影响。文献[8-9]提出利用一套精度较高的SIMU来对存放时间较久的SIMU进行标定,通过六位置转动进行误差参数标定。但该方案需要加工精度较高的包装箱或发射筒,工程中较难实现。文献[10]则对利用导弹水平、竖直和其他起竖位置来标定SIMU的可行性进行了分析,提出利用发射车从仓库到达发射点过程中停车位置的信息来辅助在线标定。
另一方面,利用低精度转台的旋转来实现对SIMU的标定已成为近年来学界研究的热点之一[11-13]。其核心思想是以SIMU的陀螺来跟踪转台角运动而不依赖于转台自身的转位精度,利用SINS输出的速度误差信息来实现对SIMU的标定。在此基础上,本文以某型倾斜式发射制导弹箭武器系统为应用背景,对利用发射架机动代替低精度转台转动,进而实现制导弹箭SIMU在架标定的方案进行了研究。
1 弹载捷联惯导系统误差模型
1.1 捷联惯组误差模型
在进行SIMU在架标定过程中,将用到如下坐标系:i系:惯性坐标系,相对惯性空间静止的坐标系;e系:地理坐标系,选取标定所在地的东北天方向作为地理坐标系;n系:导航坐标系,选取标定所在地东北天方向的地理坐标系作为导航坐标系;b系:载体坐标系,即弹载子惯导坐标系,选取弹载SIMU的右前上方向作为载体坐标系;bm系:发射架坐标系,即主惯导坐标系。在制导弹箭武器系统中,车载定位定向系统安装在发射架上,选取定位定向系统的右前上方向作为发射架坐标系。当定位定向系统中的高精度惯导系统(主惯导)与弹载捷联惯导系统(子惯导)平行安装时,b系的姿态与bm系姿态完全相同;当主子惯导系统间存在安装误差时,如果直接用主惯导姿态初始化子惯导姿态,将引入子惯导的初始姿态误差。本文先不考虑主子惯导系统间的安装误差以进行公式推导,而在文末对其影响进行讨论和处理。
对于长时间整弹存储的制导弹箭,由于不对其弹载SIMU进行拆卸,仅利用发射架的有限机动,相对其库存前标定结果进行修正,其标定误差模型需要进行简化,忽略稳定性相对较好的陀螺和加计的失准角误差系数[14],则陀螺和加计的误差模型可分别写为:
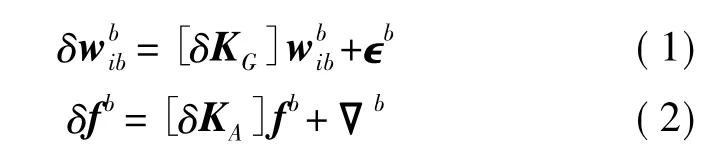
1.2 捷联惯导系统简化误差方程
捷联惯导系统的速度和姿态误差微分方程表示为[15-16]:
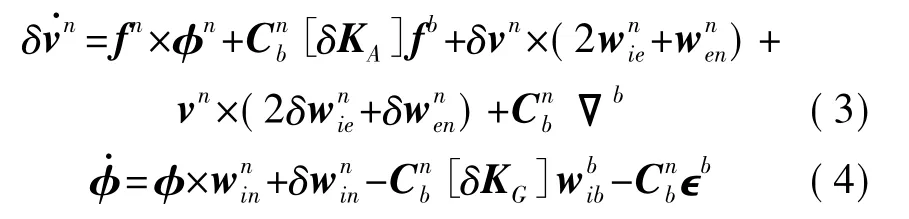
经过杆臂效应补偿后,在架标定过程中的SIMU相对地球只有角运动,而没有线运动,故vn==0,
而且在进行在架标定时,当地的地理纬度可以通过GPS精确测得,可认为δL=0,在保证姿态误差角为小角的条件下,其与地球自转角速度的乘积项可忽略,则用于SIMU在架标定的速度和姿态误差微分方程可简化为:
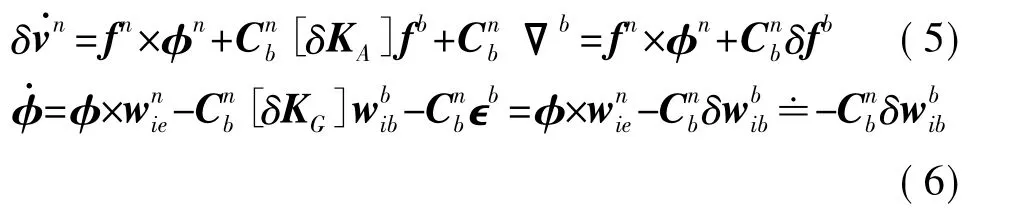
2 捷联惯导系统在架标定方案
从式(5)和式(6)可见,SINS的速度误差变化率和姿态误差变化率是SIMU器件误差的函数。不同于通常求解微分方程的系统级标定方案,本方案仅利用发射架机动前后SINS的速度误差变化率构造代数方程来求解陀螺和加计的误差参数。这将使得标定过程的计算量大为降低。
由式(5)可知,机动前后的速度误差变化率可分别表示为:
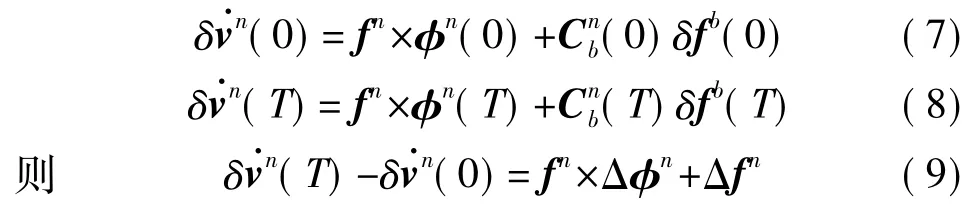
设机动前SINS姿态误差初值为φ0,机动后的姿态误差为φ=φ0+Δφ,因此,
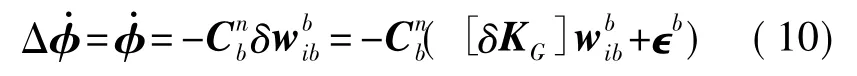
当发射架以较快角速度机动时,在较短的机动时间内(不超过10 s),由陀螺随机常值漂移引起的姿态误差变化量完全可以忽略,则上式可进一步简化为
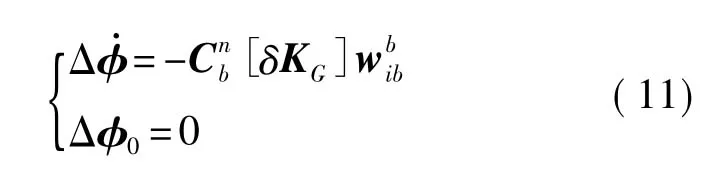
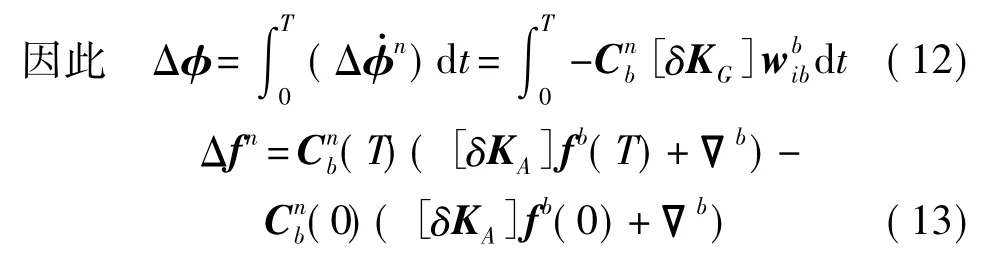
式(9)、式(12)、式(13)即是本标定方案的基本方程。
在选取机动方案时,尽量只激励较少的误差参数,以避免不同参数间的相互干扰。为了使式(12)积分相对简单,也为了弄清基本机动对误差参数的激励关系,我们只考虑发射架绕单轴旋转机动条件下速度误差变化率的变化量与SIMU误差参数的关系。
2.1 单俯仰机动
设弹载SINS的初始姿态为[0 0 0]T,发射架只进行绕俯仰轴的机动,末了姿态为[θ 0 0]T,则一次单俯仰机动引起的速度误差变化率的变化量为
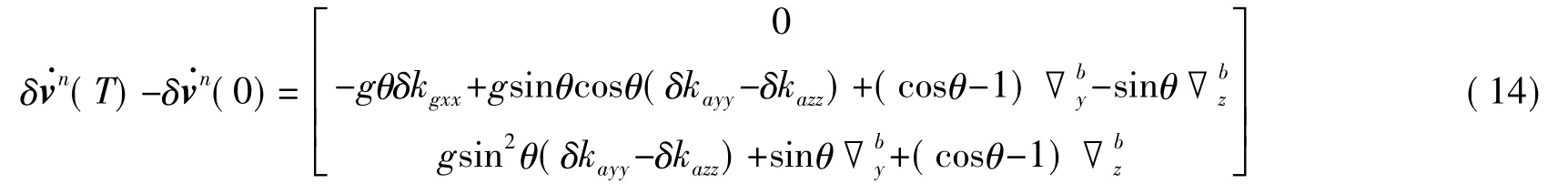
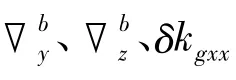
2.2 单偏航运动
工程中,制导弹箭发射架的偏航机动只能在发射架先完成俯仰机动,达到一定俯仰角度(如θ0)并稳定后,才能单独进行。因此设弹载SINS初始姿态为[θ00 0]T,定义偏航角北偏东为正,绕n系-zn轴旋转,末了姿态为[θ00 ψ]T,则一次偏航机动引起的速度误差变化率的变化量为
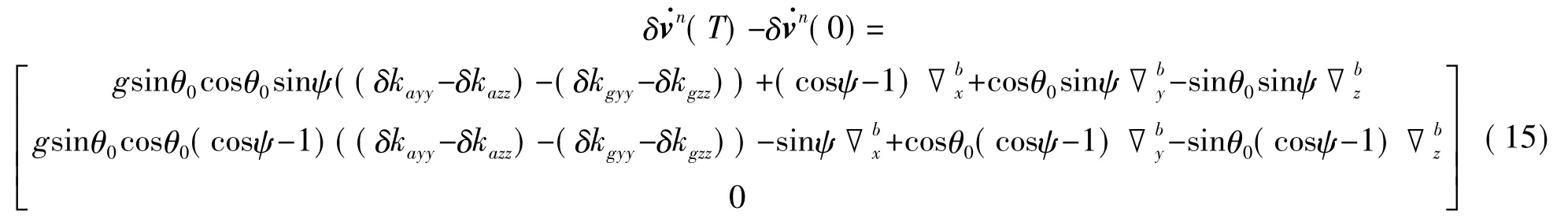
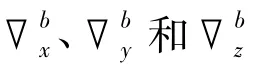
2.3 单横滚运动
为了标定SIMU纵向轴陀螺误差参数,需要对弹载SIMU进行横滚机动,因此只利用发射架的俯仰和偏航机动无法实现对其有效激励,因此可以考虑对弹载SIMU添加一个横滚环架使其能绕纵轴旋转,专门进行标定。对于利用横滚隔离环进行载体横滚解耦的制导弹箭,则可利用该环进行伺服旋转实现SIMU标定。因此,不妨设弹载SINS初始姿态为[0 0 0]T,定义横滚角右倾为正,绕b系yb轴旋转,末了姿态为[0 γ 0]T,则一次横滚机动引起的速度误差变化率的变化量为
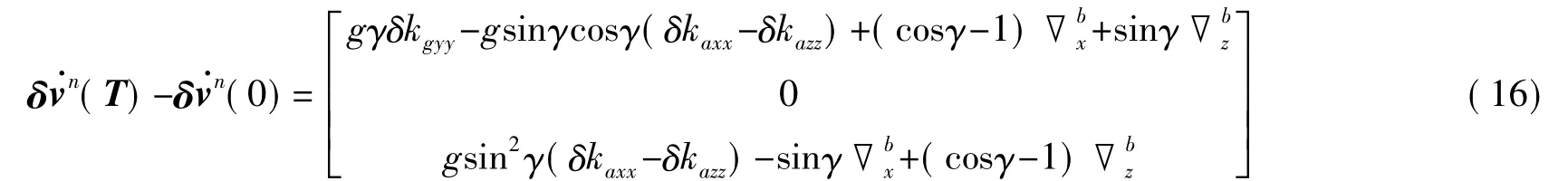
从式(16)可以看出,横滚机动可以激励4个加计参数和1个陀螺参数,能标定的参数或参数组合为 δkgyy、(δkaxx-δkazz)、、。同样,在完成发射架单俯仰和单偏航机动条件下,只需一组横滚机动即可标定 δkgyy和(δkaxx-δkazz)。
3 标定方案仿真及分析
现将式(14)、式(15)和式(16)可激励参数统一列表如表1所示。

表1 发射架激励与可标参数关系表
数学仿真参数设置如下
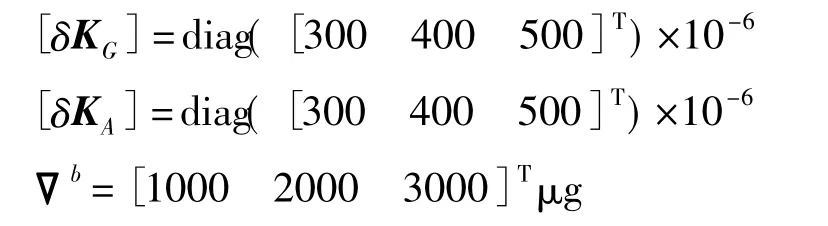
当不考虑陀螺随机常值漂移和初始姿态误差时,仿真中的发射架机动过程描述如下:发射架在初始姿态位置静止10 s,然后进行10 s的匀角速度单轴机动,然后再静止10 s。其中俯仰机动共进行两次,初始姿态为[0° 0° 0°]T,末了俯仰角分别以θ1、θ2表示;在一定俯仰角(以 θ0表示)基础上进行偏航机动一次,即初始姿态为[θ00°0°]T,末了姿态为[θ00°ψ]T;如果弹载SIMU可以通过内部标定环实现横滚机动,则增加一次横滚机动,即初始姿态为[0° 0° 0°]T,末了姿态为[0°γ 0°]T。
仿真中弹载SIMU中陀螺和加计的输出频率是100 Hz,导航信息输出频率是10 Hz。由于发射架没有线运动,因此在扣除惯导的杆臂速度后,弹载惯导输出的速度信息就是速度误差信息,因此,使用发射架机动后1 s(20 s~21 s)和机动前1 s(9 s~10 s)的弹载惯导速度误差相减,就得到机动前后惯导速度误差变化率的变化量,从而得到一组量测数据。由于俯仰机动只能激励4个参数,因此,理论上只需两次零初始姿态条件的不同俯仰角机动就可完成标定。再加上一次偏航机动得到的一组量测数据,就可构造6个等式的方程组,从而对6个参数进行标定。如果可进行一次横滚机动的话,就可以构造8个等式的方程组,从而对8个参数进行标定。现将仿真结果列表如表2所示。

表2 在架标定仿真结果
通过比较不同的机动方式可以得出,在零初始姿态和忽略陀螺随机常值漂移条件下,只需要进行两次俯仰机动即可实现对上表前四行参数的标定,增加一次具有俯仰角基础上的偏航机动,即可实现对上表前六行参数的标定。偏航机动对前四行参数标定结果几乎没有影响,这反映了俯仰机动和偏航机动对参数激励的相对独立。在相同的机动时间内,俯仰角越大和偏航角越大,误差参数的标定精度越高。在无横滚机动的条件下,δkgyy、δkgzz无法分离,且误差相对较大。在增加横滚机动条件下,δkgyy、δkgzz可以有效分离,且估计精度较高。在三种角机动条件下,加计刻度系数误差都不能有效分离,这反映了在其对速度误差变化率变化量的影响方式相同,因此还需要进一步的约束条件才能实现参数分离。
4 讨论
该标定方案利用机动前后速度误差变化率的变化量对捷联惯导主要参数进行在架标定。理论上,单轴机动所激励的参数越少越好(如通过转动90°或180°等特殊角度),这样可以避免不同参数的相互干扰。但在工程实际中,发射架的机动角度有限,不可避免多个参数相互影响,这就需要进行多次单轴机动,对其测量利用最小二乘等方法求解。考虑到发射架的机动精度达角秒级,因此可以不考虑运动误差对标定精度的影响;如果发射架机动精度不高,还可利用最小二乘平差和多次迭代标定等技术来提高参数的标定精度。
同时,由于本标定方案忽略了地球自转角速度、陀螺漂移误差和弹载惯导的初始姿态误差(即相对发射架主惯导的安装误差)的影响,因此需要对这些误差因素的影响进行说明。
4.1 陀螺漂移残差的影响
仿真中,当SIMU存在较大陀螺随机常值漂移时,该标定方案将失效。其原因是标定方案推导过程中,假定陀螺漂移变化不大,从而采用原有陀螺漂移标定值对姿态误差变化量的影响可忽略,见式(11)。因此不仅不能利用本方案对陀螺漂移残差进行标定,相反,如果陀螺漂移残差较大时,需要采用其他方法先对该残差进行估计和补偿,如可通过在近似零初始姿态条件,静止状态下陀螺输出的角速度信息减去已知的地球自转角速度来近似,再对原有陀螺漂移标定值进行补偿或采用姿态匹配传递对准方法对该残差进行估计和补偿。而仿真表明,对于在δe=0.5°/h量级的陀螺漂移残差,可以通过提高发射架机动角速度来有效抑制其对标定结果的影响。
4.2 安装误差角的影响
从式(12)看,弹载惯导的初始姿态误差对姿态误差变化量没有影响,但如果存在较大的初始姿态误差,再与本是小量的地球自转角速度耦合,将对姿态误差变化量造成较大的影响,导致标定方案的失效。因此,对于较大的主子惯导间的安装误差角,需要先利用GMLRS发射架上装配的高精度定位定向系统对弹载子惯导进行姿态匹配传递对准,估计出主子惯导的安装误差角,从而可有效补偿子惯导的初始姿态误差。已有文献[17-18]验证该对准方案的对准精度在δφ=1 mrad量级,因此补偿后的弹载惯导初始姿态误差对本方案标定结果的影响也能忽略。
5 结论
本文以制导弹箭武器系统为应用背景,当不考虑陀螺随机常值漂移变化量和初始姿态误差时,详细推导了在发射架有限机动条件下,速度误差变化率的变化量与捷联惯组误差参数的关系。为了标定纵向陀螺刻度系数误差需要利用横滚隔离环进行辅助机动。同时,当存在较大的陀螺随机常值漂移误差和初始姿态误差时,需要先对其进行补偿再利用本方案进行标定。仿真结果验证了该方案的有效性,这为制导弹箭捷联惯组提供了一种免拆卸标定的参考方案。
[1]Gamble A E,Jenkins P.Low Cost Guidance for the Multiple Launch Rocket System(MLRS)Artillery Rocket[J].IEEE AES Systems,2001,16(1):33-39.
[2]High Mobility Artillery Rocket System(HMARS)Program Overview http://www.army-technology.com/projects/himars/
[3]Pittman D N,Roberts C E.Determining Inertial Errors from Navigation-in-Place Data[C]//Position Location and Navigation Symposium,1992.Record.500 Years After Columbus-Navigation Challenges of Tomorrow.IEEE PLANS’92.,IEEE,1992:60-67.
[4]Pittman D N,Lanier N C,LeFevre V C.Integration and Testing of a Low-Cost Land Navigator for the Army Combined Arms Weapon System(TACAWS)[C]//Position Location and Navigation Symposium,1996.,IEEE,1996:399-406.
[5]Gilmore J P,Musoff H.A Unique Self-Calibrating Redundant Inertial System[C]//Position Location and Navigation Symposium,1992.Record.500 Years After Columbus-Navigation Challenges of Tomorrow.IEEE PLANS’92.,IEEE,1992:46-51.
[6]Howard Musoff,Jerold P Gilmore.Inertial Navigation System with Automatic Redundancy and Dynamic Compensation of Gyroscope Drift Error[P].united states patent.5194872.1993-3-16.
[7]吉翠萍,雷宏杰,陈璞,郭创.激光陀螺捷联惯导系统元件误差自标定技术[J].火力与指挥控制,2006,31(11):15-17.
[8]卿立,李海强.一种中低精度捷联惯测装置的不开箱标定方法研究[J].中国惯性技术学报,2004,12(4):16-19.
[9]李海强,詹丽娟,卿立.捷联惯性测量装置在整弹上的标定方法研究[J].战术导弹控制技术,2006,53:32-36,58.
[10]祝燕华,刘建业,孙永荣,华冰.导弹射前惯测组件误差在线标定方案研究[J].系统工程与电子技术,2007,29(4):618-621.
[11]Robert M Rogers.Applied Mathematics in Integrated Navigation Systems[M].second edition,Reston:AIAA,2003.
[12]娄晓芳,译.捷联惯性导航系统标定方法[J].导航与控制,2003,2(1):75-78.
[13]严恭敏.车载自主定位定向系统研究[D].西北工业大学,2006:43-47.
[14]Morris M Kuritsky,Murray S Goldstein.Inertial Navigation[J]IEEE Proceedings of the IEEE,1983,71(10):1156-1176.
[15]秦永元.惯性导航[M].北京:科学出版社,2006.
[16]秦永元,张洪钺,汪叔华.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社,1998.
[17]秦永元,游金川,宋勇.传递对准在制导型多管火箭中的应用[J].压电与声光,2010,32(4):565-567.
[18]You Jinchuan,Qin Yongyuan,Xia Jiahe,et al.Transfer Alignment Design and Experiment Evaluation of the SINS for GMLRS Artillery Rocket[C]//6th Int.Symp.on Precision Engineering Measurements& Instrumentation,Hangzhou,China,2010.

