超声波多次回波反射法测量乙醇溶液密度研究*

杨 璇，苏明旭，蔡小舒，吴 健

(上海理工大学颗粒与两相流测量技术研究所，上海 200093)

对医药化工等许多行业而言，在线测量和控制产品的密度非常重要。目前已有很多方法和仪器可以用来测量溶液的密度，但是却很难实现在线的实时监测和反馈。超声波具有很强的穿透性，适用于非侵入式测量，已在在线测量溶液的密度上得到了应用［1］。但传统的超声测量仪器通常采用测量超声衰减值或声速的方法，以标定的方式来确定超声衰减或声速与密度的关系［2］，建立起诸如Taylor级数展开式或者改进的Urick公式等关系式［3］。这种声学特征量标定方法的局限性在于当测量样品改变时，声学特征量与密度的标定关系要随之改变;而且随着密度的变化，常会出现声学特征量对密度的不敏感区域［4］;此外当实际测量温度与标定温度不相同时，此种测量方法将会出现误差［5］，限制了此方法的测量范围。

针对以上超声衰减或声速标定方法的不足之处，本文提出利用超声多次回波反射法来测量超声波的声速和阻抗值，再根据相应的声波动理论来获得溶液的密度。此测量方法在测量过程中不需要做任何标定且为非接触式测量，是一种新颖的在线测量溶液密度的方法。

1 密度测量原理和计算方法

对于超声波传播的流体介质，可以将其声特征阻抗定义为:

ρ是流体介质的密度，c是超声波在流体介质中的传播速度。由式(1)，通过测量和换算获得声阻抗Z和声速c后，即可得到流体介质的密度。

如图1所示当平面声波以一定角度从固体介质界面入射到液体介质(具有不同特征阻抗)界面时，在边界处会发生反射和透射，pi为入射波，pr为反射波，pt为透射波。固体介质的法向声阻抗率为Zs=ρscs/cosθi，液体介质的法向声阻抗率为Zl= ρlcl/cosθt［6］。如果声波垂直入射，θi= θr= θt=0，反射系数R可由下式给出:

改写上式可得到液体声学阻抗的表达式为:

图1 声波在固液两种介质界面上反射和透射

当固体介质相对于液体介质而言具有较大的声学阻抗的时候，声波会在固体内部形成多次反射(反射系数较大甚至接近1)。通过实验手段测得多次回波信号后对其进行处理就可以得到反射系数R，再由式(3)得到液体介质的声学阻抗。如果同时测得超声信号在液体中传播的声速，根据式(1)就可以得到液体的密度，该方法对于溶液、乳浊液和悬浊液同样适用。

下文图3给出了乙醇溶液的超声多次反射回波信号，对于第Nj、Nk个回波，其幅值可用下式表示为［7］:

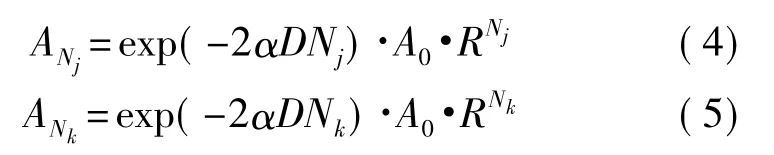
AN是第N次回波幅值，A0是初始回波幅值，α是超声波在固体介质(例如不锈钢)中的声吸收系数，R是固体介质和溶液之间的反射系数，D是固体介质的厚度。将式(4)、式(5)取对数后并相减，可得:

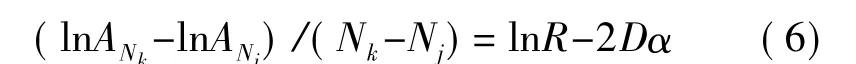
考虑多次回波的拟合(以回波次数为自变量，回波振幅的对数值为因变量)，式(6)等号左边即为所拟合直线的斜率K。如以纯水作为参照液体，可以得到:

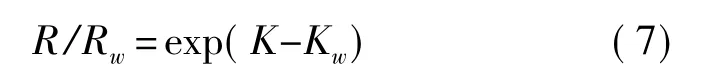
上式中，Kw和Rw分别为纯水中的直线斜率和反射系数。利用水和固体介质的已知参数(声学阻抗)，再根据式(2)，就可以确定Rw，再由实验测得的溶液和纯水中的斜率K、Kw，就能算得固体壁面－溶液的反射系数R［8］。

2 实验装置

图2(a)为密度测量装置示意图，采用了美国Panametrics公司生产的 V317－SU型(10 MHz)和V312－SU型(5 MHz)高频宽带水浸超声换能器和PR－5800型超声脉冲发射接收仪。超声换能器采用自发自收模式，而高速采集卡做A/D转换后将数据后送入与之相连的计算机，再运行自行开发的程序即可分析出被测量样品的声学特征值［9］。

在图2(a)所示的测量区示意图中，固体壁材料为不锈钢(声学阻抗为 45.72×106kg·m－2·s－1)，超声换能器和不锈钢壁之间的耦合剂是甘油，样品池内实验样品为配置的不同浓度的乙醇溶液。由于阻抗差异大，换能器发射出的大部分超声波将在不锈钢壁面处被反射，并且在壁面内部多次反射，A1是第一次回波，An是第n次回波。按照前述密度测量方法，对测得的多次回波信号进行处理就可以得到反射系数了，而采用多次回波将提高测量结果的准确性。为了保证系统信号的有效性，需要在实验过程中使用增益控制，以保证接受到的信号便于分析处理［10］。

使用图2(b)中的测量区装置来测量声速。超声波垂直入射至不锈钢和样品界面处，一部分声波反射回来形成一次回波A1，一部分透射入样品，到达第二个不锈钢壁面(即反射板)处发生反射形成二次回波A2。根据这两次回波间的时间差Δt以及两个不锈钢壁面间的距离即声程L，由c=2L/Δt可以确定声速。

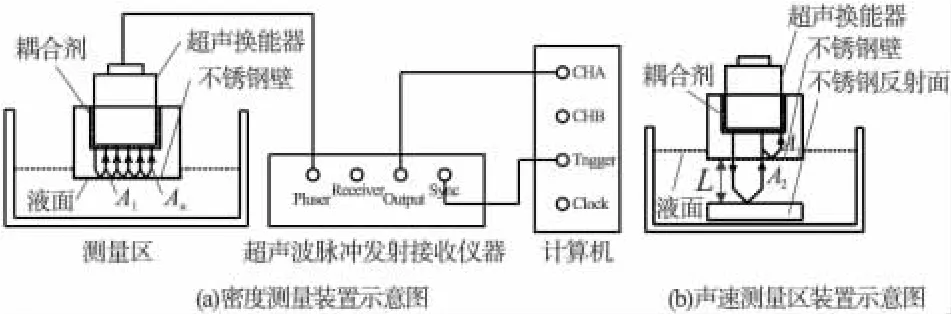
图2 测量装置示意图

3 实验数据与分析

对于由无水分析乙醇配置的不同浓度溶液进行测试。图3是实测不锈钢－乙醇溶液所得多次回波信号图，从图中可以清楚地观察到10次以上的回波信号，当超声波在溶液中传播时会发生吸收、反射、穿透等现象，所以声波振幅是依次减小的［11］。如前所述，对每一个回波信号进行快速傅里叶变换(FFT)，得到特定频率上的幅值。根据线性叠加原理［12］，将所得幅值的对数值按回波次数做线性拟合，考虑信号的信噪比，图4所示的数据处理中选取了7次回波进行拟合。对于不同种类或者不同浓度的溶液而言，由于其与不锈钢之间反射系数不同，则线性拟合后所得到直线斜率值K也不相同。

图3 乙醇溶液多次回波信号图

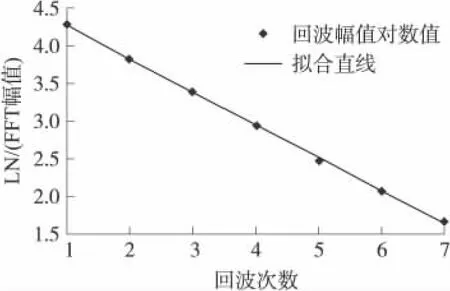
图4 回波次数与回波幅值对数值关系图

表1和表2分别给出了用中心频率为10 MHz和5 MHz的超声换能器进行测量所得实验结果。实验环境温度为25℃，纯水密度取997 kg/m3，无水分析乙醇密度为789 kg/m3。从表1结果可见，数据线性拟合的相关系数均大于0.995，样品的测量密度与配置值之间的误差不超过1.2%。表2中该误差不超过2.5%，实验结果与配置值较为符合。比较表1和表2，可见表1的平均误差水平比表2要小，表明实验中不同中心频率的超声换能器对实验精度有影响，使用10 MHz的超声换能器实验效果要优于5 MHz的超声换能器。本实验是建立在平面波理论上的，而在障碍物尺寸大小不变的条件下，使用10 MHz的超声换能器的衍射效应较小，更接近于平面波，因此测量误差较小。

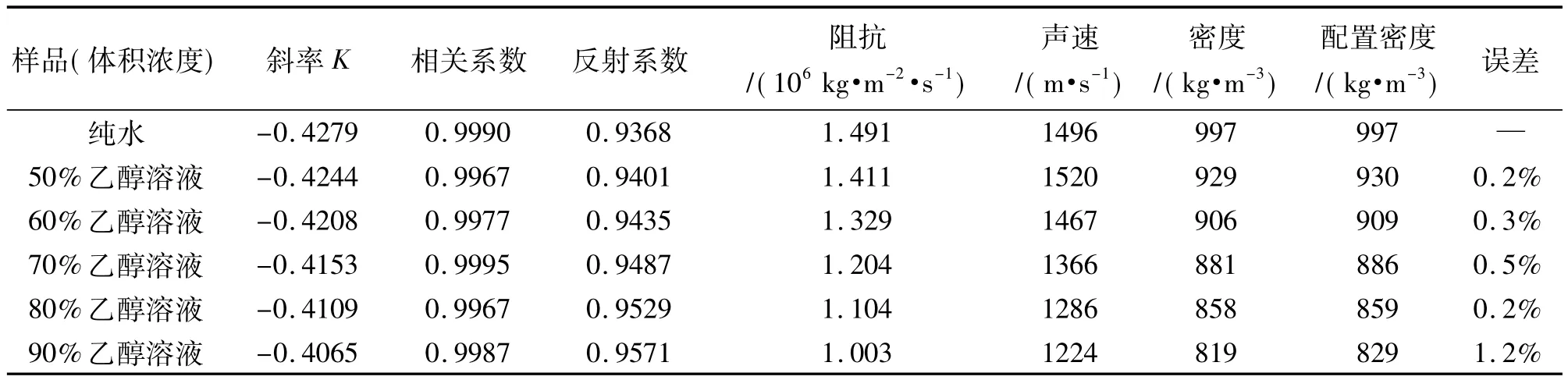
表1 不同浓度乙醇溶液实验数据(10 MHz探头)

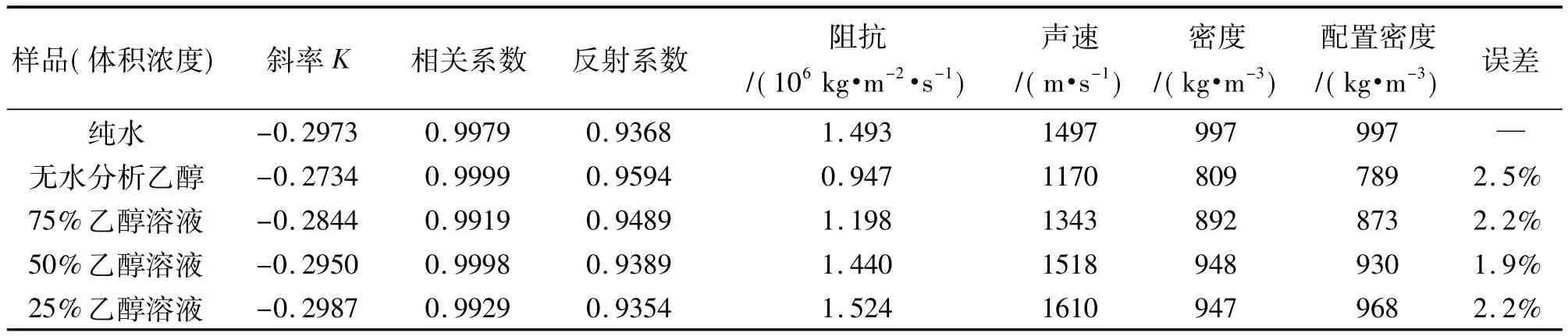
表2 不同浓度乙醇溶液实验数据(5 MHz探头)

综合表1和表2还可以看出，随着乙醇溶液中乙醇浓度的增加其声速和声阻抗会相应降低，而反射系数则会升高。由于超声波多次回波反射法只是基于不同浓度溶液中拟合数据斜率的变化，其测量结果不受超声发射功率的影响。同时由于温度因素在特征阻抗和声速中均反映并可抵消，所以该方法受温度变化影响也较小。如果能增加所测量到的回波次数并提高信噪比，则测量精度将有望进一步提高。

4 结论

本文中通过测量超声波在壁面间的多次反射回波信号来得到被测样品的声阻抗值，用超声波在不同壁面间的二次回波时差来确定溶液中的声速，从而得到了溶液的密度。本文得出结论如下:

对不同浓度的乙醇溶液进行的测量表明测得密度与理论配置值较为吻合，误差均小于2.5%。实验中使用不同中心频率的超声换能器将对实验结果的精度有一定影响，使用10 MHz的超声换能器实验效果要优于5 MHz超声换能器。

由于超声波多次回波反射法可以实现同时测量样品的声阻抗和声速、密度，具有实验装置结构简单，实时处理和分析数据且不需事先标定的优势，适合用于工业生产中液态物质(溶液、悬浊液、乳浊液)的密度在线测量。

［1］薛明华，苏明旭，蔡小舒，等.超声法测量高浓度水煤浆若干问题研究［J］.工程热物理学报，2007，28(增刊1):213－216.

［2］钱炳兴，凌鸿烈，孙跃秋，等.超声波浮泥重度测量仪［J］.声学技术，2001，20(1):42－44.

［3］Valerie J Pinfield，Malcolm J W Povey，Eric Dickinson.The Application of Modified Forms of the Urick Equation to the Interpretation of Ultrasound Velocity in Scattering Systems［J］.Ultrasonics，1995，33(3):243－251.

［4］王路，刘镇清.用声速法在线测量强酸溶液的浓度［J］.现代计量测试，1998，6(6):35－38.

［5］苏明旭，蔡小舒，徐峰.三频率声衰减法测量玻璃微珠粒度和浓度［J］.声学学报，2004，29(5):440－444.

［6］冯若.超声手册［M］.南京大学出版社，1999:54－57.

［7］Margaret S Greenwood，Judith Ann Bamberger.Ultrasonic Senor to Measure the Density of a Liquid or Slurry during Pipline Transport［J］.Ultrasonics，2002，40:413－417.

［8］薛明华，苏明旭，蔡小舒.超声波多次回波反射法测量两相流密度实验研究［J］.工程热物理学报，2008，29(8):1343－1346.

［9］尚志涛，苏明旭，薛明华，等.一种新型超声水煤浆测量装置［J］.仪器仪表学报，2007，28(8):5－8.

［10］王铭学，王文海，田文军，等.数字式超声波气体流量计的信号处理及改进［J］.传感技术学报，2008，21(6):1010－1014.

［11］董黎丽，苏明旭，薛明华，等.基于超声衰减谱的脂肪乳粒度分布测量方法［J］.过程工程学报，2008，8(1):8－10.

［12］宋寿鹏，阙沛文.超声信号的非线性行为及应用［J］.传感技术学报，2007，20(1):129－131.