基于Spline插值的分布式多速率数据帧扫描同步重构技术
吴文杰,黄大贵,董 政
(电子科技大学机械电子工程学院,成都 610054)
在大型航空发动机试验中,采用分布式多前端测控网络系统往往需测量稳态、瞬态和动态变化的各种参数[1-3];但实际测量的各参数变化速率相差大,各前端数据采集子系统的采样和扫描周期不相同,且时分制异步采集与通道并行同步采集、声像视频等各种采集方式同时存在,这些都增加了分布式网络环境下的多传感器多速率信息融合的难度。目前,多传感器信息融合算法一般都是假定在不同传感器之间具有相同的采集速率或整数倍速率[4-6],其重构算法通常采用插值和滤波算法[7-8]。而实际测试中会出现速率异步采集和非整数倍多速率采集的情况,这种情况造成的不同步问题值得研究。
本文结合分布式网络环境与现场状态监控应用特点,提出了采用样条插值重构的帧扫描同步技术,将来自各前端子系统的测量(观察)数据,同步转换为具有统一起始时刻的相同采集速率(帧速率)数据来解决同速率异步采集和非整数倍多速率采集所造成的不同步等诸多问题。
1 同步重构方法
具有代表性的分布式多传感器系统如图1所示,图中Sys(1)和Sys(2)是时分制异步的多通道数据采集子系统,Sys(3)是并行同步的多通道数据采集子系统,Sys(4)是多路闭路电视音像视频监视子系统。各Sys(p)子系统的采样方式、采集速率、测量通道数和被测信号种类不全相同,这样整个系统测量的全帧由具有不同采集速率和/或采集遍数的多个子帧组成。若时间尺度和序列长度不同,不能简单地进行数据级融合处理而是需要进行同步重构处理[9]。同步重构的过程包括:分布式网络中各子系统的时间同步、帧同步码(同步时间区间)的计算确定、各子帧的同步转换和全帧的同步(整合)重构[10-11]。
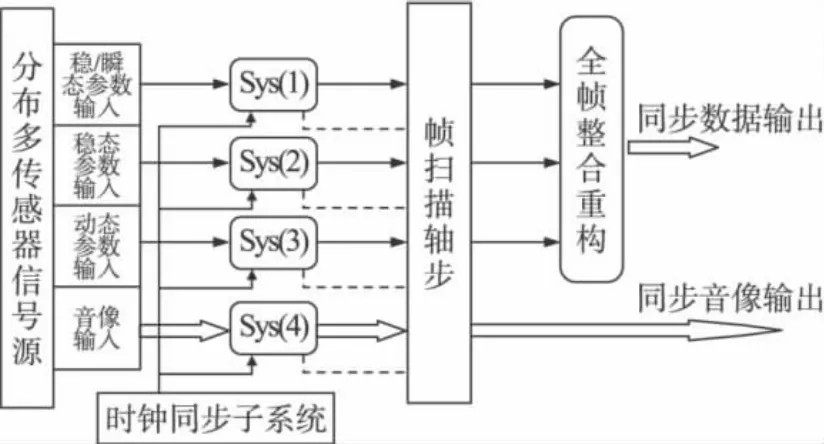
图1 分布式多传器系统帧扫描同步架构示意图
1.1 帧同步码的计算
首先将整个分布式网络与各前端采集子系统进行时钟同步[12-14],构造能统一整个系统各测量通道重构同步采集的时间区间[t0,te],区间内能较好满足被测对象对时间响应同步精度的要求。在此基础上,再进行数据(信息)的采样转换与同步重构。
设Sys(p)子系统的采样频率为f(p)s,测量通道数为M(p),通道序号为ch,采样周期为τ(p),子系统的帧采集速率为
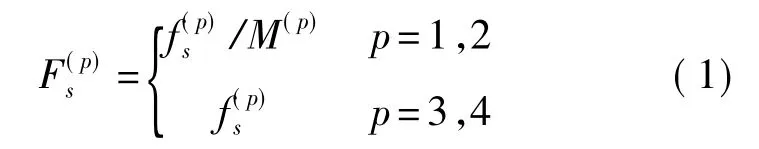
相应的帧扫描周期为
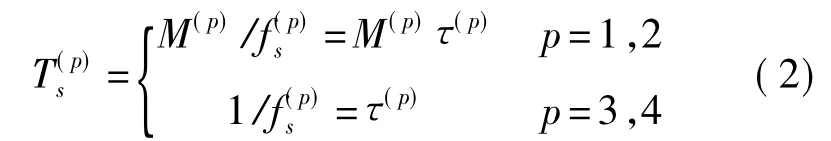
现场经传感器获取的各种物理信号x(t)通常是随时间连续变化的模拟信号[15],以速率采样,得到的离散时间序列信号为x(n)=x(nτ(p))n=0,1,…,N-1。确定帧同步码的步骤如下:
(1)设系统时间响应对同步精度的要求τ(0)≤1 ms。同步帧扫描周期=τ(0),以此周期作为统一的同步标准,对各子系统的帧速率进行重构。
(2)各子系统的帧周期。
①Sys(1)和Sys(2)采用测量M个通道顺序进行巡回采样的子系统,各测量通道获取的输出序列信号为xch(m),为原采样序列x(n)中进行M取1的抽取。由式(1)可知通道输出信号采样周期则扩大了M倍,即xch(m)=xch(Mnτ),ch=1,2,…,M。假设两子系统测量通道数为M(1)=100,M(2)=40;采样率为8 kHz,10 kHz,其采样周期为 0.125 ms,0.4 ms。
②Sys(3)子系统的各测量通道是并行同步采样方式,采样率相同且等于帧速率。假设采样率为=5 kHz,子帧扫描周期为 0.2 ms。
③Sys(4)视频子系统为PAL制信号,设帧速率为=25 Hz,帧(扫描)周期为 0.4 ms,设帧同步后的整个序列长度为Nf,则同步区间时段为Nf。令各子系统的帧扫描序列的同步倍数an、帧周期为,有
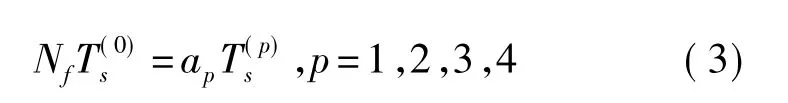
将Sys(1)~Sys(3)各子系统帧周期值代入上式,得
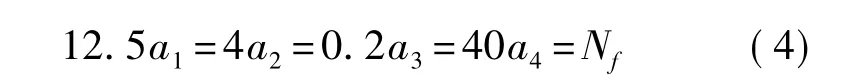
上式有无限多个整数解,为此要引入约束条件。由于系统要求同步时间间隔分辨率为τ(0)≤1 ms,而同步采样的数字量化效应存在δ=±1个数字误差。因此,要求同步重构的序列长度为

此式为约束条件的不等式。将δ和τ(0)代入上式,得Nf≥1/0.001=1000,则a4=Nf/40=25,能满足全帧扫描同步到1 ms精度要求。计算出各子系统的同步时段内序列长度为:a1=80,a2=250,a3=5 000。则时间同步区间Nf=1 s,这样可采用区间为1 s的时间同步码,给各子系统测量通道获取采样数据,每隔1 s打上相应的帧扫描同步标志,其中,对于Sys(4)采集的视频数据帧,需打上帧扫描同步标志。
1.2 时分制异步采集子系统的通道数据同步
对时分制异步采集子系统Sys(1)和Sys(2),由于各通道输入采集的是同一序列信号x(n)=x(nτ)。各测量通道输出序列xch(m)=xch(Mnτ)为
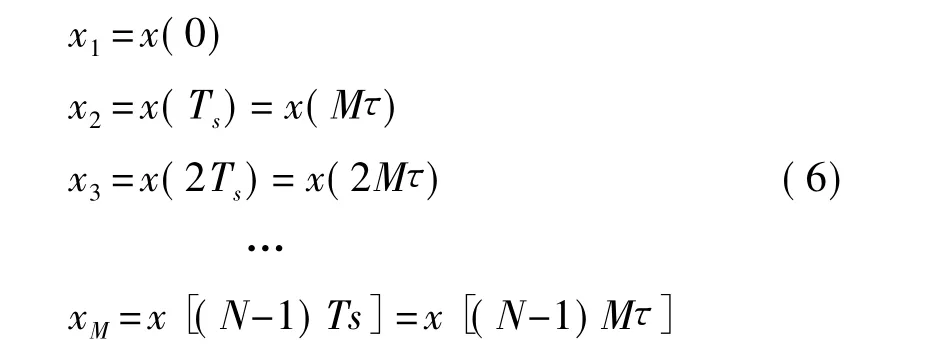
第1通道输出序列的延时为零,因此,可作为时分制采集系统各测量通道同步重构的统一起始时刻,将各测量通道的输出序列统一转换成与第1通道起始时刻(和/或帧扫描同步尺度区间)相同的序列。下面采用Spline插值算法来重构实现。
1.3 Spline样条插值重构
三次样条插值函数s(t)在子区间[ti-1,ti]上的表达式为[7]:
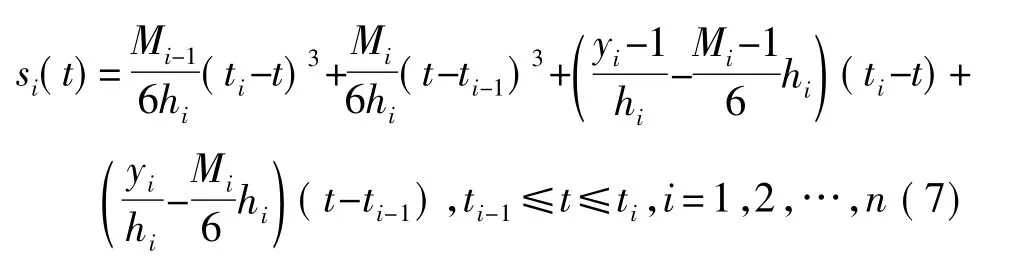
式中hi=ti-ti-1,Mi=s″(ti),本文采用满足第一种边界条件来计算样条插值。采用Spline样条插值对分布式多速率扫描同步重构技术的步骤为:

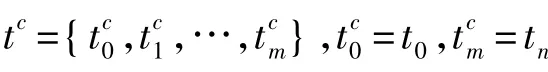

在同一个帧同步时段内,可将原函数的帧采样率Fs,转换为具有其m/n倍的同步帧速率。当m>n时,提升采样率;当m<n时,则降低采样率。m/n可以是有理数,因此可实现非整数倍的速率转换。
(3)通过各离散时间点值计算出三次样条函数si(t)中各系数,得到函数s(t)表达式。应用Spline插值函数,通过重采样的时间序列tc,实现了同步重构原函数f(tc)。
2 仿真验证
本节采用数值仿真实例来验证验证Spline样条插值来实现的同步重构是否准确和有效。为检验在分布式网络环境下,Spline样条插值来实现的同步重构是否准确和有效,各前端以不同采样率获取输入序列信号。用正弦信号、非线性多项式函数来模拟瞬态过程参数,白噪声来模拟现场干扰的影响。采用序列误差的评估准则,表明同步重构的准确度。
2.1 标准信号源与随机噪声信号
用正弦信号源模拟采集系统的平稳的或周期谐波,正弦标准信号

式中幅度A=100,频率f0=10 Hz,初相位为 φ0=0。在同步区间[t0,te],用同步帧速率对其x1(t)进行采样,得采样后的相应同步离散标准正弦序列信号源x1(n)。
用非线性的多项式函数来模拟随时间上升变化的瞬态过程信号,连续时间多项式模型标准信号:
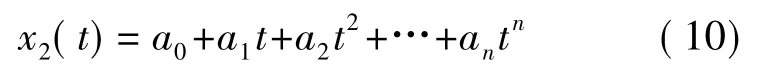
式中多项式的阶数设为n=3,各系数设为a0=1,a1=10,a2=90,a3=100。在同步区间[t0,te],以同步帧速率对其x2(t)进行采样,得到采样后的同步标准多项式序列信号源x2(n)。
用白噪声来模拟现场干扰的影响,正态分布(高斯分布)的随机噪声信号:
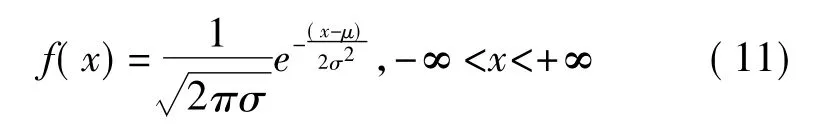
式中,μ为均值,σ为方差,x为随机变量,f(x)为概率密度。
2.2 评估准则
在帧序列同步窗口区间[t0,te]范围内,输入的标准信号源为x(t),设定同步重构要求的帧速率进行采样,得到作为标准的原始输入信号序列x(0)(n)。设各子系统以不同采样率对同一输入信号x(t)进行采样,得到帧序列信号为x(p)(m),经同步重构后得出的相应信号为(n)。这些信号是不含噪声的序列,若采样序列X=x(0)(n),第p号子系统同步重构得到序列为Y(p)=(n),则可用重构序列信号误差的平方和进行评估,其第p号子系统的单位样本长度重构误差平方和为
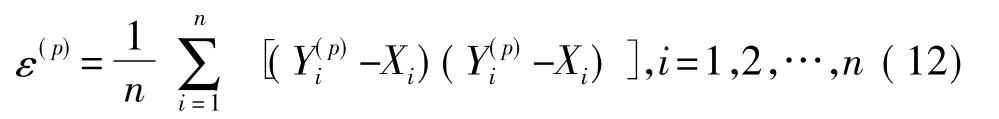
显然ε值越小,表明重构误差也越小,其所用的重构方法准确、有效。因此,用序列的单位样本长度误差平方和作为重构方法的评估准则依据。在某些时候,也可用协方差来评估。
2.3 仿真验证
下面各仿真实例均用Matlab仿真计算[6]。
2.3.1 Sys(1)和Sys(2)各测量通道输出信号序列的同步重构仿真验证
分别用正弦信号、“正弦+随机(白噪声)”信号、多项式模型信号和“多项式+随机”信号,作为采样的输入信号序列,经Spline样条插值重构后,分别得到 Sys(1)子系统第1,20,40,60,80 和100 通道,和Sys(2)子系统第 1,8,16,24,32 和40 通道为例的同步重构(未消除对正弦波边界效应影响),输出重构序列的误差平方和,数据分别如表1和表2所示。
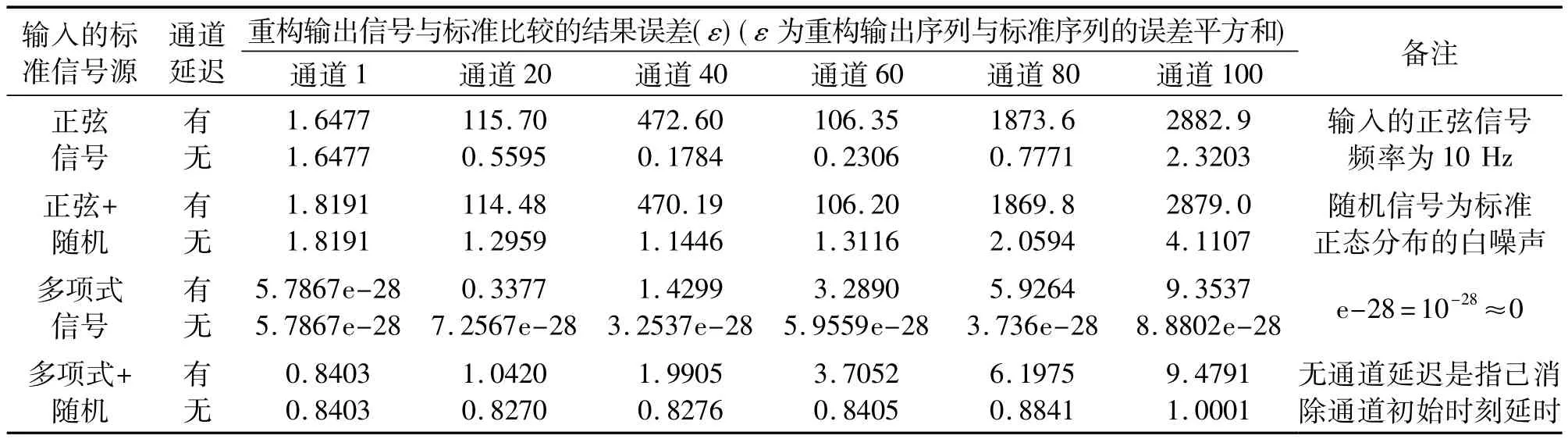
表1 Sys(1)用Spline插值的同步重构误差(↑12.5倍帧速率)
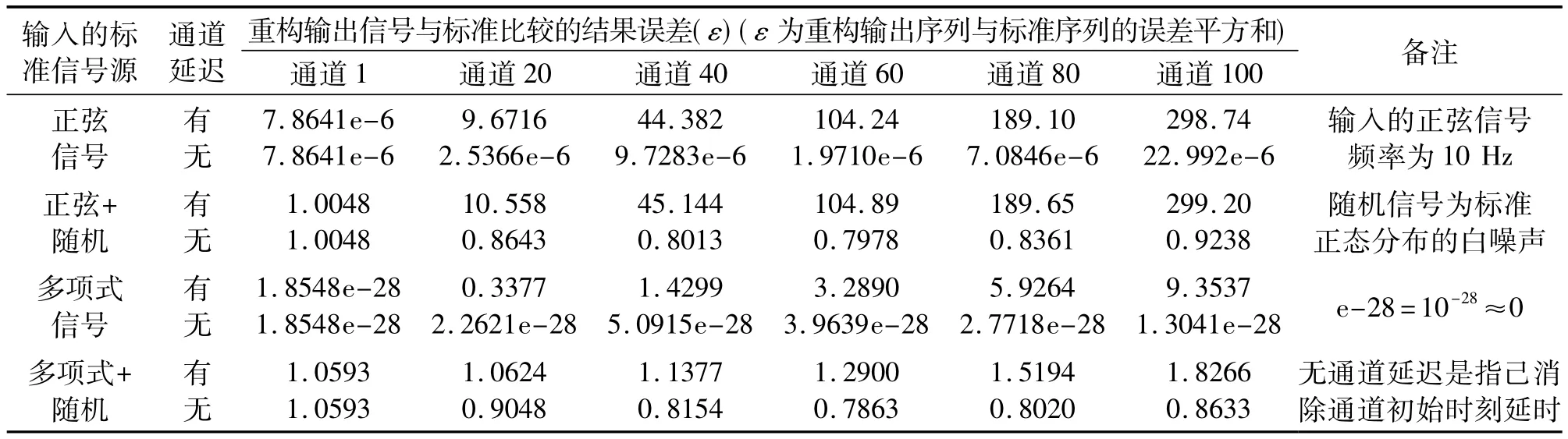
表2 Sys(2)用Spline插值的同步重构误差(↑4倍帧速率)
2.3.2 对Sys(3)测量通道输出信号序列在不同速率下的同步重构仿真验证
Sys(3)子系统各测量通道是并行采样的,各通道相互间不存在通道延迟,其系统采样率即为帧速率,因此仅需进行同步的速率变换即可。仍分别用上述同一信号序列作为标准输入,在多种采样速率下,经Spline样条插值重构,其重构输出的各同步序列的误差平方和,数据见表3。
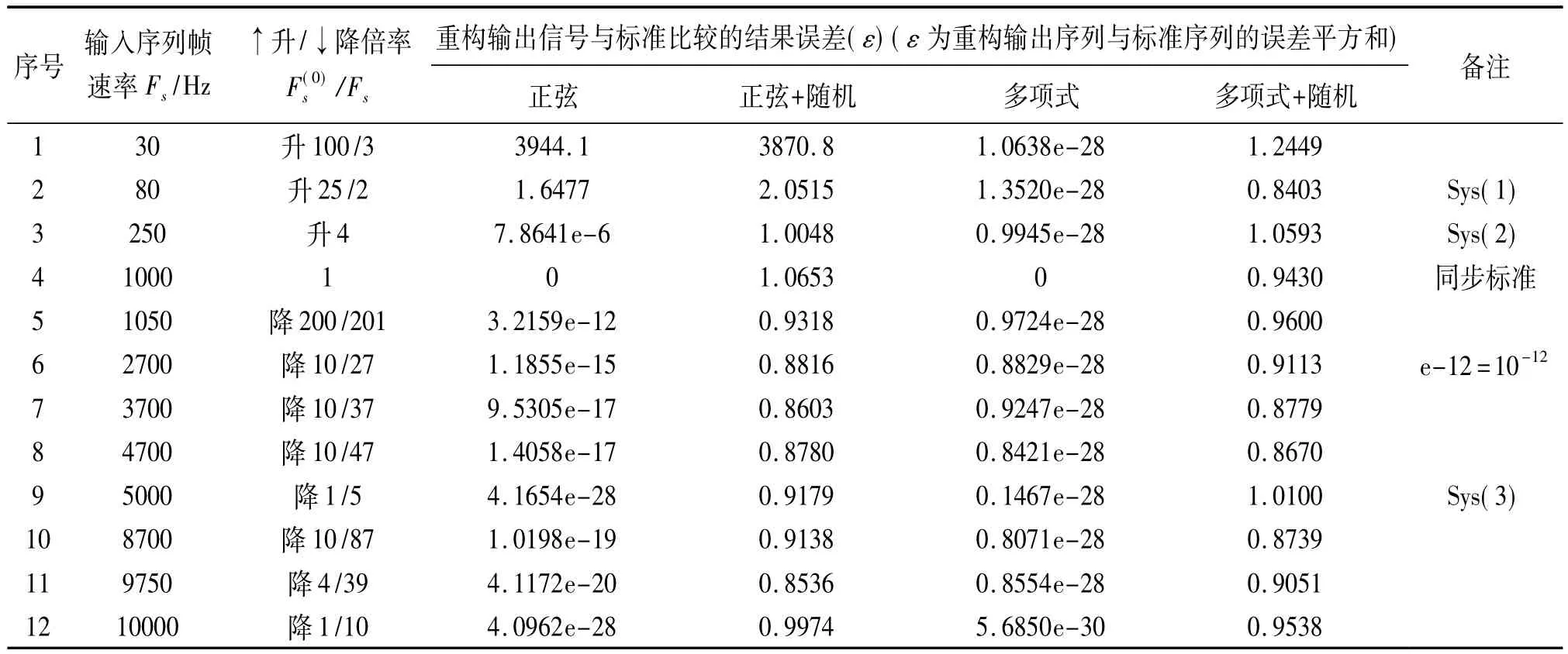
表3 Sys(2)用Spline插值的同步重构误差(↑↓帧速率)
2.4 仿真结果讨论
2.4.1 对升帧速率时分制系统各测量通道的同步重构结果的误差分析
表1和表2列出了在两不同速率的采集子系统中,在统一的同步区间内,经Spline插值重构输出的各测量通道序列信号误差的平方和数据。通过比较后得出如下结果:(1)在时分制采集系统中,测量通道间的初始延迟对正弦波重构误差的影响最大,对多项式信号的影响较小。两种输入信号的重构误差,都随着提升帧速率倍数的降低而有显著地减小。(2)Spline通过时序移位重构是消除测量通道间初始延迟的有效方法;消除通道延迟后的重构误差近似为零,既准确又很有效。(3)随机干扰信号的引入,与通道延迟相比,对重构误差的影响不大。其消除通道延迟后重构误差数值的增减,一般在高斯分布的方差范围内变化。(4)Spline对正弦波的升帧速率的重构,还存在着因截断边界效应引起的重构误差。通过剔除重构输出序列末端少量数据点,可消除边界效应误差,进一步提高重构准确度。
2.4.2 Sys(3)子系统在不同采样率下同步重构结果的误差分析
从表3可见,对降帧速率的Sys(3)子系统,随帧速率的进一步提高,重构误差一般有所减小。但若以整数倍抽取,越接近于1的整数倍抽取,其重构误差将变得更小。无论输入的是何种不含噪声的纯净信号,其重构输出的误差平方和都很小(约在3.215 9×10-12以下);引入噪声后,其重构误差的数值约增加了相应噪声的方差。
3 结论
鉴于输入序列信号以及重构输出序列信号的最大值均在100以上,而重构误差的单位长度平方和接近于零值,或与幅值相比其相对误差极小。通过上述仿真验证及其对同步重构结果误差分析表明:本文采用的系统同步架构适应分布式网络环境的能力强,提出的帧扫描同步重构方法的同步重构准确度高,对输入的各种信号适应性也都很好,能将多种不同采集速率和/或不同起始时刻的测量数据,有效地转换为能较好满足系统对同步时间响应精度和同步重构准确度要求的,具有同一起始时刻的相同帧速率。这为多传感器多速率信息的数据级融合创造了条件,保障了整个系统全帧同步重构的实现分验证了本文Spline同步重构方法的准确性和有效性。
[1]Zhang L,Wu X L,Pan Q,et al.Multiresolution Modeling and Estimation of Multisensor Data[J].IEEE Trans.on Signal Processing,2004,52(11):3170-3182.
[2]文成林,周东华.多尺度估计理论及其应用[M].北京:清华大学出版社,2002:58-233.
[3]吴文杰,秦东兴.基于时钟同步的航空发动机分布式试验测控系统的研究[J].燃气涡轮试验与研究,2004(02):46-48.
[4]陈大光.航空发动机设计手册第1册:通用基础[M].北京:航空工业出版社,2000:93-96.
[5]张善文,雷英杰,冯有前.MATLAB在时序列分析中的应用[M].西安:西安电子科技大学出版社.2007:82-96.
[6]吴文杰.高空台分布式测控系统设计及关键技术应用研究[D].成都:电子科技大学,2004.
[7]LU Pong-jeu,Zhang Ming-chuan,Hsu Tzu-cheng,et al.An Evaluation of Engine Faults Diagnostics Using Artificial Neural Networks[C]//Proceedings of ASME TURBO EXPO 2000,Munich.Germany,2000.
[8]彭靖波,谢寿生.ELman回归神经网络在航空发动机故障诊断中的应用[J].航空发动机,2007,33(2):46-49.
[9]陈恬,孙建国,郝英.基于神经网络和证据融合理论的航空发动机气路故障诊断[J].航空学报,2006,27(6):1014-1017.
[10]宋新民,王格芳,冯锡智.基于信息融合技术的复杂系统故障诊断研究[J].仪器仪表学报,2006,27(6):1764-1765.
[11]贺鹏,李菁,吴海涛.网络时间同步算法研究与实现[J].计算机应用,2006,23(2):15-17.
[12]Jiang Li-ying,Zhang Yan,Li Zhong-hai,et al.Aero-Engine Fault Diagnosis Based on Multi-Scale Independent Component Analysis,Wavelet Analysis and Pattern Recognition[R].2009.ICWAPR 2009:118-122.
[13]Chen Dungen,Ding Guangbin.Multi-Concurrent Fault Diagnosis Approach for Aeroengine Based on Wavelet Fuzzy Network[C]//Control and Decision Conference,2009.CCDC’09,17 -19 June 2009:5421-5426.
[14]Liao Wei,Wang Hua,Han Pu.Neural Network Modeling of Aircraft Power Plant and Fault Diagnosis Method Using Time Frequency A-nalysis[C]//Control and Decision Conference,2009.CCDC’09.Jun,2009:353-356.
[15]Zhu Rui,Wu Dezhi,Liu Zhirong,et al.Aeroengine Modules Performance Deterioration Modeling and Assessment[C]//2010 IEEE International Conference on Industrial Engineering and Engineering Management(IEEM):1626-1630.

