成形刀设计算法及其刃形修正的基本原则
张志梅 安虎平
(1.兰州交通大学,甘肃 兰州 730070;2.兰州城市学院机械检测与故障诊断研究所,甘肃 兰州 730070)
成形刀设计算法及其刃形修正的基本原则
张志梅1安虎平2
(1.兰州交通大学,甘肃 兰州 730070;2.兰州城市学院机械检测与故障诊断研究所,甘肃 兰州 730070)
根据成形加工原理,运用几何分析法建立了成形车刀切削刃廓形设计的基本计算公式。按照最常用的棱体成形车刀和圆体成形车刀两种类型分别建立刀具廓形的计算式,运用这些廓形计算式求得刀具廓形各组成点尺寸,这些尺寸可达到任意精度的要求。将计算式用于加工给定工件的成形刀廓形设计,取得了满意的效果,也为刀具廓形的 CAD设计软件的二次开发提供数学模型。从工件轮廓形状的形成和刀具制造两方面分析了产生加工误差的原因,并给出了进行刀具廓形修正的原则。
成形车刀;设计;计算法;廓形修正;原则
切削加工是利用刀具切除被加工零件上多余材料的方法,是现代制造业中最重要和最基本的加工方法。同时刀具是各种机床实现切削加工的直接执行者,可见刀具在金属切削加工中的地位和作用。生产实践证明,刀具改进与变更机床、夹具相比,其投入小、周期短、见效更快。因此善于制造业生产的经营者,不但看重机床、夹具附具等硬件和软件改进,更重视刀具的设计、改进和生产,以充分发挥刀具的内在潜力,方能达到生产利润的最大化。目前成形车刀在汽车、拖拉机、轴承等生产中应用较多,主要用在自动或半自动车床上大批量加工内、外回转体零件的成型表面。常用成形车刀的加工质量稳定,生产率高,有助于简化机床和夹具的结构,降低生产成本。随着科学和生产技术的发展,对先进设备的零件精度要求不断提高,而高性能刀具材料的出现和应用,还需要更为精确的刀具设计方法,才能满足这种高精度制造的要求。虽然作图法设计成形车刀廓形比较直观,但由于图线过于繁多、作图误差难以避免,设计精度较低,所以只能满足普加工通精度要求〔1〕。为满足高精度加工要求,本文结合作图分析,用计算法设计成型车刀,可达到更高精度,还可为成形车刀的CAD设计提供数学模型。
(一)成形车刀设计的计算法
从原理来看,成形车刀的廓形设计可有三种方法:即作图法、计算法和查表法〔2-4〕。下面按棱体和圆体成形车刀分别讨论计算法。由于成形车刀切削刃的廓形宽度与相应被加工零件的廓形宽度相等,因此,成形车刀廓形设计主要任务是确定各对应点的廓形深度。
1.棱体成形车刀设计计算法
如图1所示,为棱体成形车刀分析计算图,已知条件为:零件廓形半径1r、2r、3r……;其中1r为最小半径,切削刃上该对应点为基准点。设基准点处成形车刀的前、后角分别为fγ、fα。刀具切削刃上任一点处垂直于直棱后刀面的法平面内的廓形深度为xP,零件上相应于该点的半径为xr( =1,2,3,……)。由图可知:则
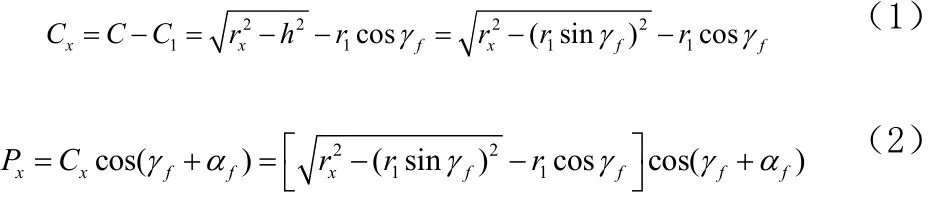
式中xP——棱体成形车刀在法平面内对应于零件上 x点处的廓形深度;
rx——零件上各组成点的半径。
在式(2)中只要根据选定的前角fγ和后角fα及刀刃基准点处的工件半径1r,给出不同的工件轮廓半径xr( =1,2,3,……),即可求得垂直于基准点处后刀面的垂直距离xP( =1,2,3,……),然后作图求得法平面内刀刃廓形。
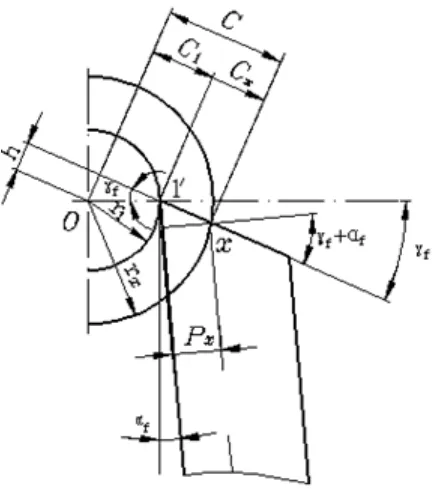
图1 棱体成形车刀计算分析图
2.圆体成形车刀设计计算法
如图 2所示,为圆体成型车刀的计算分析图,图中已知条件为:零件廓形半径1r、2r、3r……;,刀具廓形最大半径为R,设基准点处成形车刀的前、后角分别为fγ、fα,刀具切削刃上任一点 处的径向廓形深度xP应等于刀具廓形最大半径R与该切削刃点所在位置处的半径Rx之差,即Px=R−Rx。
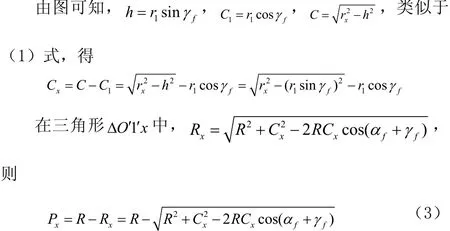
式中xP——圆体成形车刀在径向平面内对应于零件上 x点处的廓形深度。
在式(2)、式(3)中,1r、fγ、fα、R均为已知,因此,两种刀具的廓形深度都决定于对应点处的零件廓形半径xr。
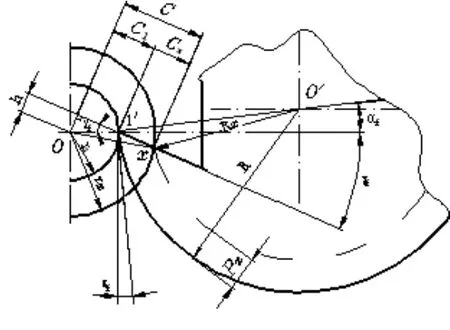
图2 圆体成形车刀计算分析图
3.成形车刀计算法设计举例
成型车刀设计的主要任务是确定刀具廓形各组成点,确定的依据是工件轮廓各组成点,方法是根据计算法公式求得刀具测量平面上相应点的的廓形尺寸。关于工件上计算尺寸的选择均按所给值的平均值考虑,对于精度要求不高的自由尺寸,可直接将未注公差的尺寸作为计算尺寸。现以如图3(a)所示的工件为例,介绍用圆体成形车刀加工时的刀具设计计算方法。
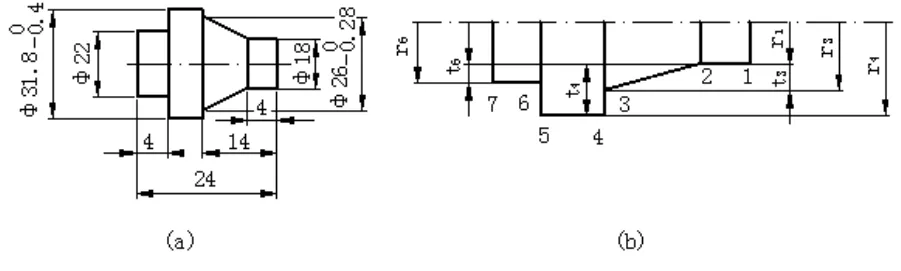
图3 成形零件
已知工件廓形和尺寸如图3(a)所示,在C1336型单轴自动车床上加工,选定刀具外径D=68mm(即R=34mm),刀具装置高度 h=5mm,刀具刃磨高度hp=1 1mm,则刀具廓形尺寸可按如下步骤设计。
(1)确定刀具上前角γf和后角αf
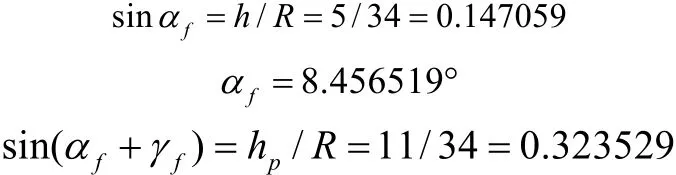
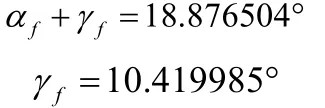
(2)确定工件上各组成点的半径尺寸。根据工件轮廓取其组成点如图3(b)所示,xr表示各组成点的半径,从零件图上可知各组成点的半径尺寸如表1所示。

表1
(3)计算刀具上廓形尺寸,根据公式(3)可得xR和xP(当x=1,2,3,4,5,6,7时)的值,如表2所示。
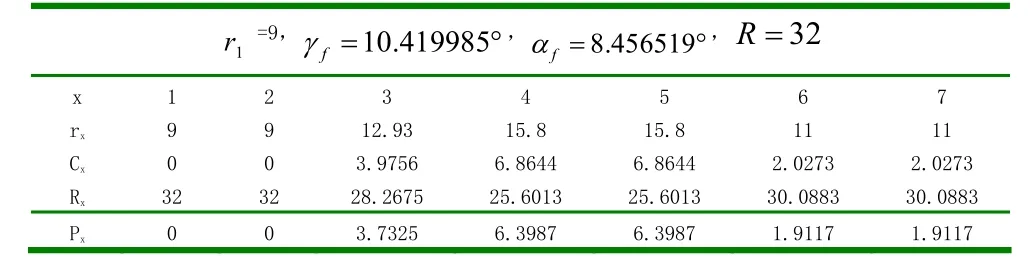
表2
(4)绘制圆体成形车刀,根据已知条件和表 2的计算数据,可设计加工给定零件所需要的成形车刀如图 4所示,其中尺寸公差按有关成形车刀公差决定方法确定。
同样根据已知条件,并利用公式(1)、(2)可用计算法设计棱体成形车刀来加工该零件,只不过刀具廓形是在垂直于后刀上面直棱的法平面中的廓形。
用计算法求成形车刀廓形可达到任何所需要的精度,一般可根据实际需要而定。计算过程中的数据应精确到小数点后四位数以上,计算最终结果通常长度尺寸精确到0.01mm,角度精确到1′。
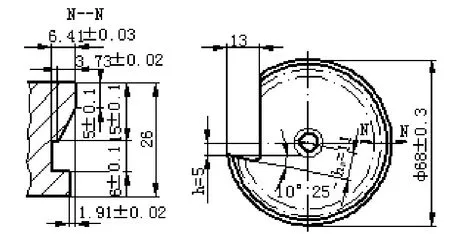
图4 圆体成形车刀
(二)成形车刀廓形修正
计算和作图的实践都表明,通常求得的刀具廓形与工件廓形存在很大的差异,其原因可从工件廓形的形成及刀具制造两方面进行分析。
1.成形车刀廓形修正的原因
刀具设计主要是确定成形车刀的刀刃廓形,应从工件廓形的形成和刀具制造两方面进行考虑。生产实践中回转体成形工件的廓形深度是在其径向平面内测量,而工件的廓形在切削加工中是在刀具的前刀面上形成的;圆体成形车刀的实际廓形是在其径向平面上测量的,主要原因是便于制造;棱体成形车刀的廓形深度是在垂直于刀具后刀面侧棱的平面上测量的。
由此可知,只有当刀具的前角和后角都等于零度时,工件廓形的形成平面与刀具前刀面重合,成形车刀的廓形与工件廓形才有可能完全相符。但刀具与切削原理知识告诉我们,后角等于零,即α=0°的刀具是不能工作的,没有实用价值。当前角等于零度时,即γf=0°的刀具切削刃不够锋利,排屑卷屑也不轻快。对于具有实用价值的成型刀具,都应当有合理的前角和后角,但此时的刀刃形状就不同于工件在径向平面内的形状,刀具的廓形深度小于工件上相应的廓形深度而产生误差。为保证车刀能切除正确的工件廓形,所以在设计时就必须考虑对刀具廓形进行修正计算。
2.刀刃廓形修正计算的目的
修正计算的目的在于刀具设计时确定刀刃各组成点,圆体成形车刀的修正在于决定刀具廓形上各组成点的半径 xR( =1,2,3,……),棱体成形车刀设计修正在于决定刀具廓形各组成点相对于基点在法平面内的垂直距离。
3.修正计算的原则
由于成形车刀刀刃上各点的前、后角是变化的,这就决定了成形车刀修正计算的复杂性。要对刀刃廓形的各点都进行修正计算,这将给设计工作造成很大的困难。为使修正工作简单起见,可仅对有代表意义的轮廓点进行修正,这些点就是工件廓形的组成点。
(1)工件廓形组成点的选择原则
①对于工件的直线廓形部分,可取直线两端点作为其组成点。
②对于工件的曲线廓形部分,除应取其两端点作为组成点外,还应视工件加工精度要求的高低,在曲线部分的中间再取若干点作为组成点。若工件加工精度要求高应适当多取一些点,反之,可适当少取一些点。
(2)刀具廓形的连接方法
①若工件廓形为直线形,则刀具的廓形亦用直线连接。
②若工件的廓形为曲线形,则刀具的廓形应按工件上相应组成点用光滑的曲线顺序相连。
(三)总结
成形刀具是用来加工回转体零件成形表面的非标准的专用刀具,工件表面形状的复杂性决定了刀具廓形多种多样。保证被加工工件所要求的精度是成型刀具设计时要着重考虑的问题。本文通过对成型刀具设计计算法的较深入探讨,获得了成形刀具高效精确设计的计算方法,同时为成型刀具的计算机设计提供了数学模型。通过对工件轮廓形状的形成原理和刀具制造过程两方面的分析,得到了产生误差的基本原因,并提出了进行刀具廓形修正的原则。
[1] 叶伟昌.成形车刀的设计与制造[M].中国农业机械出版社,1982.6.
[2] 陆剑中,孙家宁.金属切削原理与刀具[M].机械工业出版社,2004.10.
[3] 王娜君.金属切削刀具课程设计指导书[M].哈尔滨工业大学出版社,2000.1.
[4] 张吉君.成形车刀设计中的关键问题分析[J].机械设计与制造,2008.2.
TG702
A
1008-1151(2011)06-0112-02
2011-03-18
张志梅(1965-),女,甘肃永登人,兰州交通大学后勤管理处工程师,从事机电技术研究。

