标量拟解析近似方法模拟立方体的异常电场

张金会，孙建国，张亚东

(1．吉林大学 地球探测科学与技术学院，长春130026 2．国土资源部 应用地球物理综合解释理论开放实验室，长春130026;3．安徽省勘查技术院，蚌埠233005;4．长庆油田公司勘探部，西安710021)

标量拟解析近似方法模拟立方体的异常电场

张金会1，2，3，孙建国1，2，张亚东4

(1．吉林大学 地球探测科学与技术学院，长春130026 2．国土资源部 应用地球物理综合解释理论开放实验室，长春130026;3．安徽省勘查技术院，蚌埠233005;4．长庆油田公司勘探部，西安710021)

拟解析近似方法是一种求解积分方程的一种近似方法，它可以处理强散射或者大扰动的电磁散射问题，在计算过程中避免了传统微分数值方法解决问题时所遇到的大型矩阵或大型代数方程组的求解。孙建国［5]将其引入直流电场的积分方程中，并给出了求解异常电场积分方程的标量拟解析近似公式。在以前的研究中，已经验证了均匀场中异常球体的拟解析近似解的精度，这里对均匀场中的立方体异常体进行数值模拟，得到了直流电场中异常立方体模型的标量拟解析近似解。由于复杂地电模型可以用立方体的组合进行模拟，因此对立方体异常电场拟解析近似解的研究，为三维直流电场中复杂地电模型的快速正反演模拟打下了基础。

积分方程;拟解析近似;直流电场;立方体

在2005年J．Sun推导出直流电场的标量拟解析近似的理论公式基础上，作者用标量拟解析近似对均匀场中的异常立方体进行研究。不同的立方体的组合，可以对复杂异常体进行模拟。当有多个异常体组合模拟复杂异常体时，异常立方体直接的异常电场会受到其它异常体所产生的二次场的影响，因此在进行模拟时，还要考虑异常体所产生的二次场之间的相互影响。作者对单独异常体的拟解析近似方法研究，为复杂地电模型的研究打下了基础，为三维直流电场中的复杂异常的正反演模拟奠定算法基础，可以加快三维电法勘探的进程，具有较高的实际意义。

1 基本方程及公式

J．Sun在其文章中给出标量拟解析近似方法的理论公式，作者利用其理论公式，推导得到拟解析近似方法在实现过程中的具体实现细节部份。

在进行三维异常体数值模拟时，积分采用三维高斯积分进行计算，并对积分中出现的格林函数的奇异性进行了处理，采用处理方法简单，不增加运算量的挖去法［18]，在控制挖去小体积限度的基础上，得到了很好的计算效果，实现了拟解析近似方法在直流电场模拟中的应用。

一次场中异常体内部二次直流电场的积分方程［13]为:

异常体外部的积分方程［13]为:

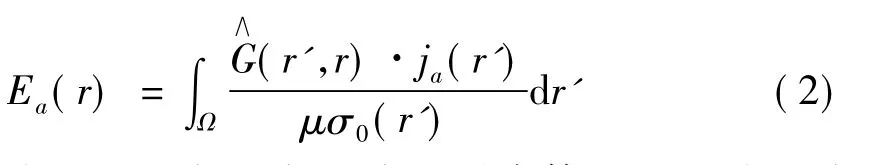
在上面的方程中Ω表示异常体，ja(r)为二次电流密度，由式(3)给出:

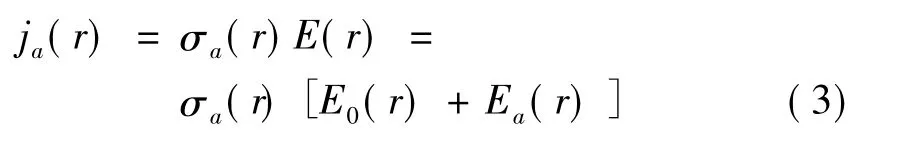
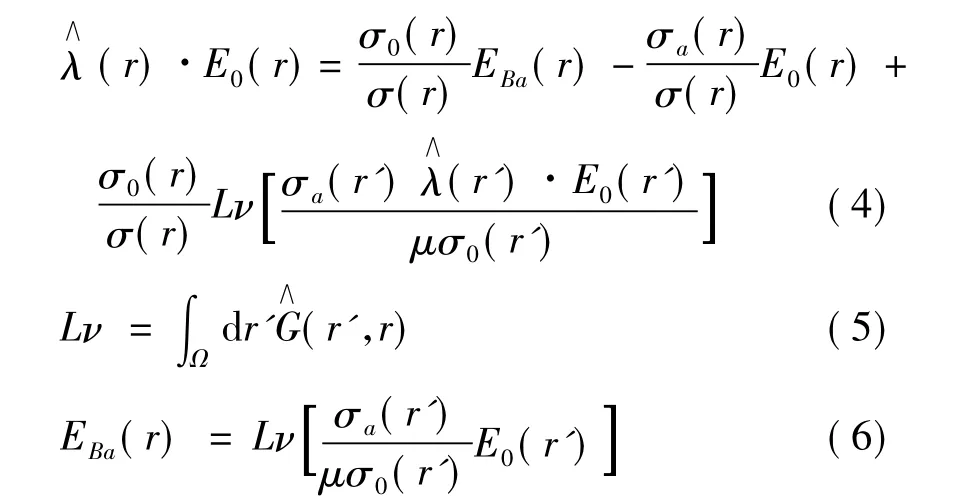
其中EBa(r)为Ea(r)的Born近似;(r'，r)为并矢格林函数，由式(7)给出

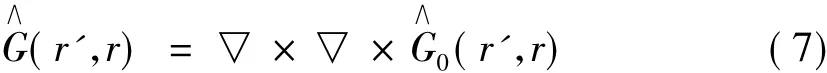
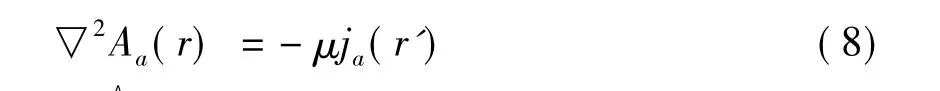
J．Sun［13]于2005年通过假设电反射张量为0阶张量，令:

其中 Ι为单位张量，得到了方程(4)的解:

通过对式(11)进行整理，可以得到:

在式(12)中

将式(12)代入到式(1)中，可以得到:

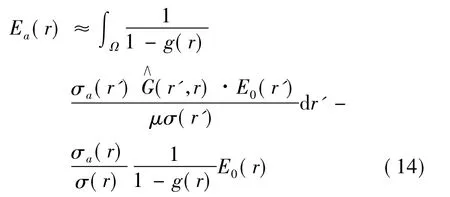
将式(14)得到的Ea(r)代入式(3)，可以得到ja(r)，将ja(r)代入式(2)中，即可得到异常体外部的异常电场:

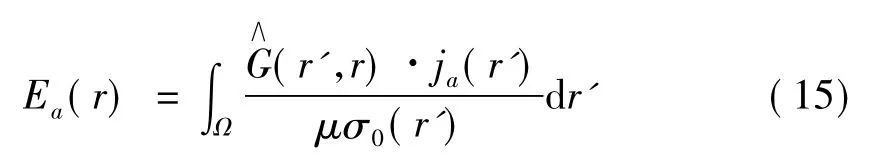
通过方程(4)，我们可以建立拟解析近似的迭代方程(16)［13]:

其中m是迭代数。令

利用方程(16)，当异常体电导率同围岩相比变化剧烈，即大扰动时，拟解析近似解不能得到想要的结果，我们可以通过式(16)的拟解析近似的迭代解得到满意的结果。在一般情况下，迭代次数m在不超过5的情况下，我们就能得到满意结果。

2 标量拟解析近似立方体异常体电场值计算

很多矿体可以由立方体组合进行近似，选取立方体异常进行研究，得到的异常体为立方体时的异常电场。在研究中给定异常体为立方体，利用标量拟解析近似方法进行计算，求出异常电场的拟解析近似解，并与Born近似解进行比较，选取的均匀场场源中的异常立方体进行计算。立方体边长为100 m，中心坐标为(0 m，0 m，0 m)，通过背景介质和异常电导率变化，可以得到不同的模型。异常体外部异常电场计算点，关于立方体中心对称分布在z=400 m处沿x方向。针对六种不同背景介质电导率与立方体异常电导率的模型，分别进行计算均匀场中不同电导率的外部电场。地电模型见图1。

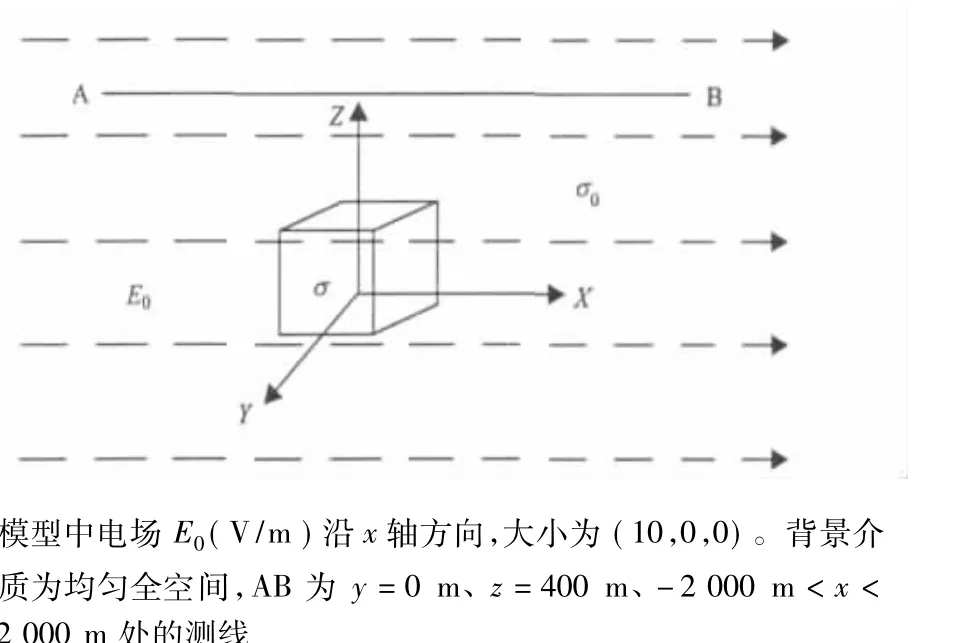
图1 均匀场中异常立方体模型示意图Fig．1 Model of anomalous cube in the uniform field

针对于均匀场中的异常立方体，我们进行了下面几组不同电导率的模型的试算。

(1)从下页图2、图3可看出Born近似解与拟解析近似解相差很小，与异常球体表现出的现象相同。

(2)后面的图4、图5都是高阻立方体。由异常体引起的电场的Born近似解与拟解析近似解相差很大，这是由于Born近似解没有考虑二次电场对异常电场的影响。当二次电场对异常电场影响较大时，使得拟解析近似解的数值较Born近似解高。

(3)图2至图7(见后面)中的曲线，给出了均匀场中不同背景的电导率，与异常电导率立方体模型的异常电场Ea的x、z分量。由均匀场中的球体的计算结果分析，可以得出图中的拟解析近似解比Born近似解更接近实际结果。

3 结论

积分方程法具有直接对异常体区域进行数值积分的优点，避免了传统数值方法解决问题时所遇到的求解大型矩阵或大型代数方程组。利用标量拟解析近似方法可以对直流电场的积分方程进行求解，作者在本文对异常体为立方体时的异常电场进行了标量拟解析近似数值模拟，该方法对于其它形状的异常体也同样可以适用，如椭球体、圆柱体等。作者通过对均匀场中的异常立方体进行的标量拟解析模拟，表明标量拟解析近似方法具有很强的适应性。当异常体电导率变化较大时，可以通过对标量拟解析近似解进行迭代仍可以达到很好的效果，这表明该方法可以用于大扰动问题的模拟。立方体异常体的空间组合可以用来模拟复杂分布的地下矿体，本文作者对立方体异常的拟解析近似研究，为解决复杂地电模型提供了借鉴，初步表明了该方法具有处理复杂地电结构的模型的能力。作者通过对直流电场标量拟解析近似方法实现的研究，为三维直流电场的快速正反演模拟，提供了快速的精确度高的数值模拟方法。

图2 σ0=1．0 S，σa=0．01 S时异常电场曲线图Fig．2 Whileσ0=1．0 S，σa=0．01 S，the anomalous electrical field curves

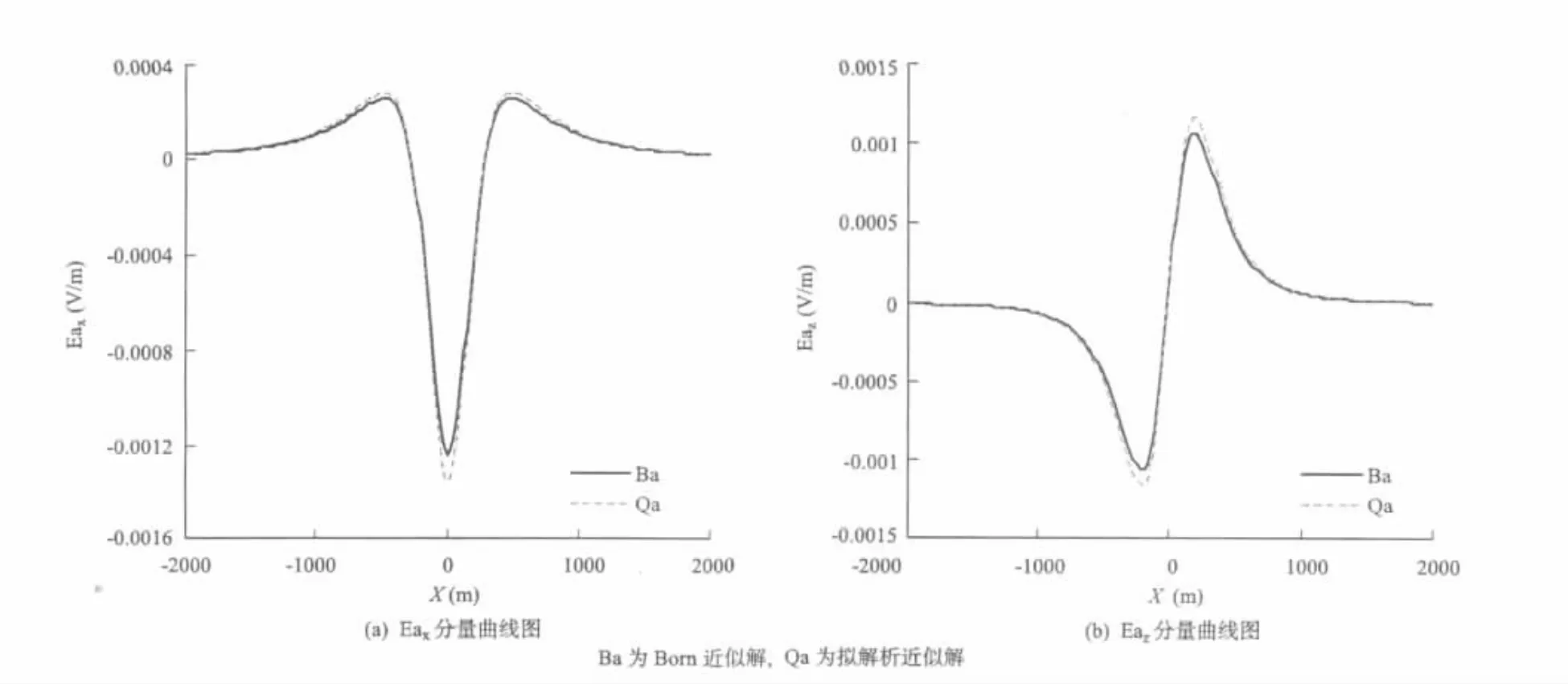
图3 σ0=1．0 S，σa=0．01 S时异常电场曲线图Fig．3 Whileσ0=1．0 S，σa=0．1 S，the anomalous electrical field curves

图4 σ0=1．0 S，σa=－0．9 S时异常电场曲线图Fig．4σ0=1．0 S，σa=－0．9 S，the anomalous electrical field curves

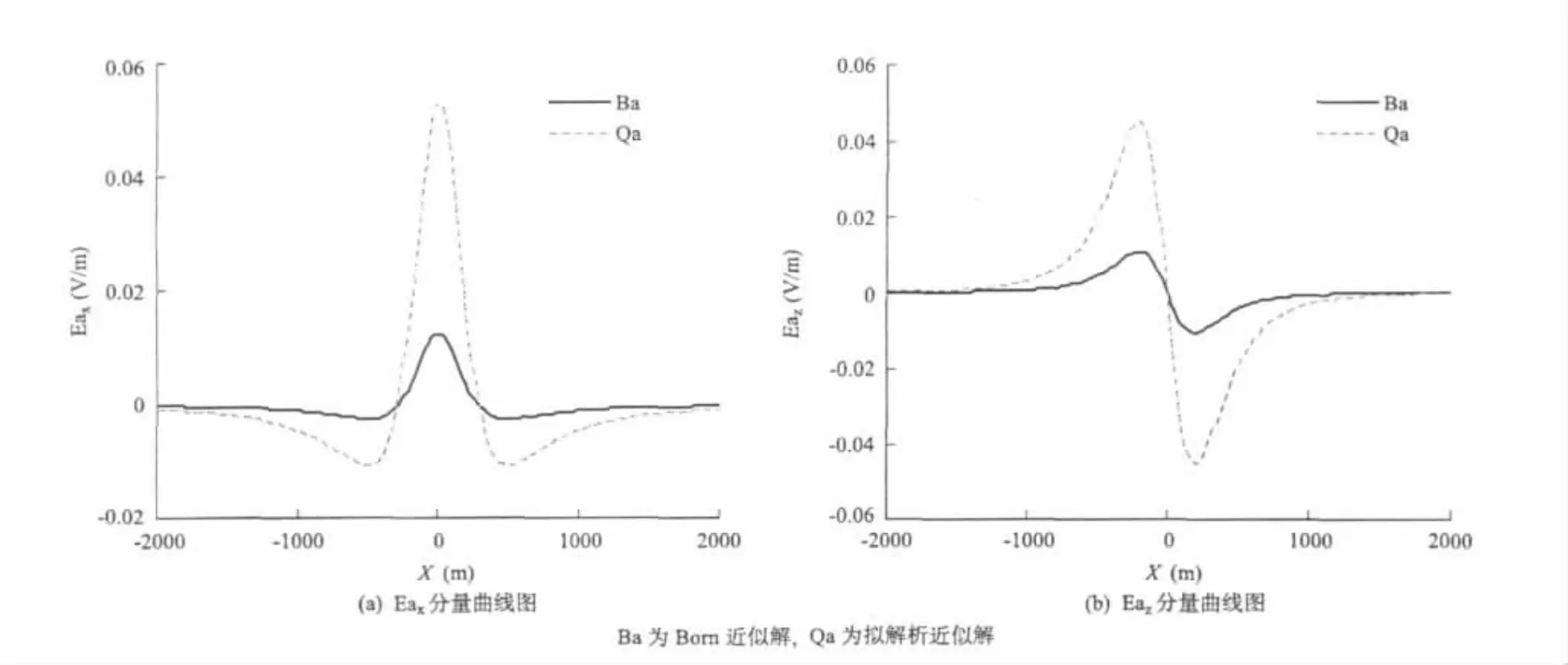
图5 σ0=1．0 S，σa=－0．99 S时异常电场曲线图Fig．5σ0=1．0 S，σa=－0．99 S，the anomalous electrical field curves

［1]HABASHY T M，GROOM W R，SPIESR B．Beyond the Born and Rytov Approximations:A Nonlinera Approach to Electromagnetic Scattering［J]．Journal of geophysical research，1993，98(B2):1759．

［2]ZHDANOV M S，FANG S．Quasi－liner approximation in 3－D eledtromagnetic modeling［J]．Geophysics，1996，61(3):646．

［3]ZHDANOV M S，FANG S，HURSAN G．Electromagnetic inversion using quasi－linear approximation［J]．Geophysics，2000，65(5):1501．

［4]ZHDANOV M S，DMITRIEV V I，FANG S，et al．Quasi－analytical approximations and series in electromagnetic modeling［J]．Geophysics，2000，65(6):1746．

［5]孙建国．声波散射数值模拟的两种新方案［J]．吉林大学学报:地球科学版，2006:863．

［6]刘宁，孙建国．起伏地表条件下的声波散射数值模拟的积分方程法［J]．吉林大学学报:地球科学版，2007:61．

［7]陈丽虹，孙建国，王忠仁．拟线性近似方法在2_5维电阻率正演中的应用［C]．中国地球物理学会第十七届学术年会，昆明:云南科技出版社，2001．

［8]陈丽虹，孙建国．地球物理反演的拟线性近似方法综述［J]．地球物理学进展，2002，17(3):464．

［9]孙建国．稳定电流场的电位反射函数［C]．中国地球物理学会第十九届年会．南京:南京师范大学出版社，2003．

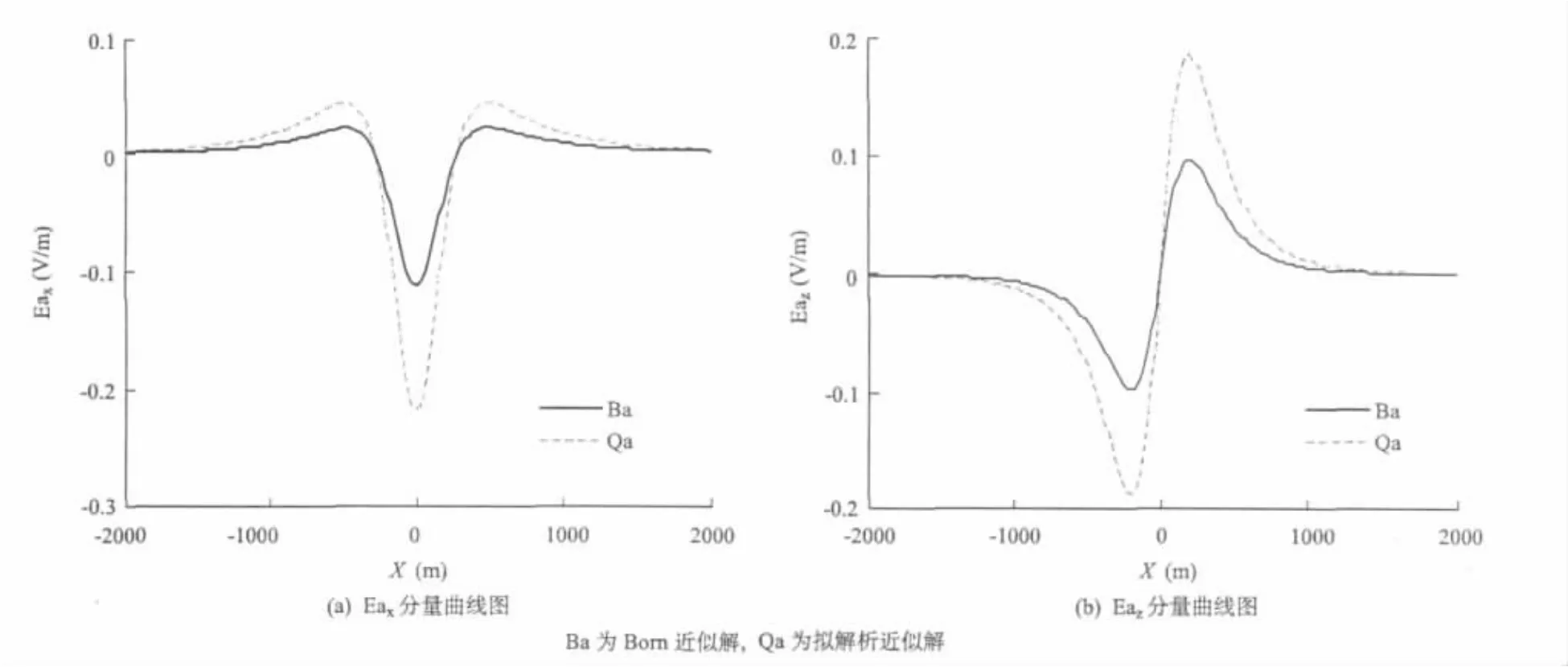
图6 σ0=0．1 S，σa=0．9 S时异常电场曲线图Fig．6σ0=0．1 S，σa=0．9 S，the anomalous electrical field curves

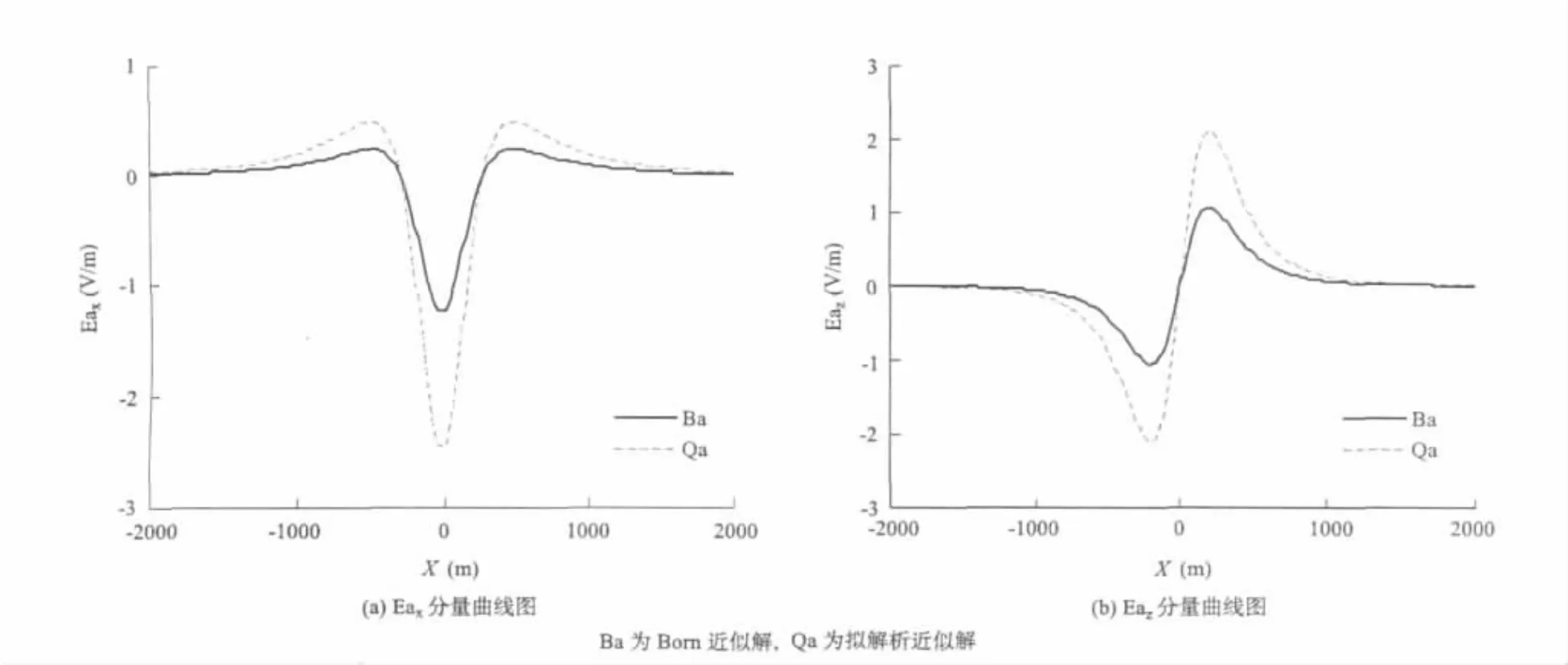
图7 σ0=0．01 S，σa=0．99 S时异常电场曲线图Fig．7σ0=0．01 S，σa=0．99 S，The anomalous electrical field curves

［10]孙建国．稳定电流场数值模拟的拟线性近似［C]．中国地球物理学会第二十届年会，西安:西安地图出版社，2004．

［11]陈丽虹，孙建国．稳定电流场的拟线性近似方法研究［J]．石油地球物理勘探，2004，39(5):589．

［12]孙建国．直流电位场数值模拟的拟解析法［C]．中国地球物理学会第二十届学术年会，西安:西安地图出版社，2004．

［13]SUN J．On the electrical reflectivity tensor in d．c electric field modelling［J]．Geophysical Prospecting，2005(53):411．

［14]孙建国．稳定电流场拟解析近似精度分析［C]．中国地球物理学会第二十一届年会．长春:吉林大学出版社，2005．

［15]孙建国．稳定电流场拟解析近似的数值评价［C]．中国地球物理学会第二十二届年会，成都:四川科学技术出版社，2006．

［16]傅良魁．电法勘探教程［M]．北京:地质出版社，1983．

［17]张金会，孙建国．直流电场拟解析近似精度分析与评价［C]．中国地球物理学会第二十四届年会．北京:中国大地出版社，2008．

［18]张金会，孙建国．格林函数的奇异性处理［J]．地球物理学进展，2009，24(6):2106．

P 631.3

A

1001—1749(2011)02—0147—06

0 前言

国家自然科学基金项目“40574052”;国家高技术研究发展计划(863)(2006AA06Z109);国家重点基础研究发展计划(973)(2007CB209603)

2010－09－28改回日期:2010－12－27

张金会(1980－)，男，河北衡水人，博士，研究方向为直流电场模拟。

近年来我国资源形势日益严峻，大规模的经济建设对金属矿的需求越来越大，对于资源的需求应该立足于国内，因此要加大国内金属矿勘探的力度。在金属矿勘探中，电法勘探占有重要地位，研究直流电场快速数值模拟，对于推进电法勘探的发展有着重要的意义。三维直流电场数值模拟的方法很多，大致可以分为微分方法和积分方法。在传统的数值方法中，都会遇到大型矩阵或求解大型线性代数方程组的问题，这对计算机硬件要求高，计算周期长。尤其是在复杂地质条件下，这些问题更为突出，所以寻求快速精确的数值模拟方法，一直是地球物理工作者的研究重点。积分方程法在解决三维直流电场问题中有其优点，如积分方程法只需对异常体进行计算，而不需要对背景区域进行计算，微分方程法在计算过程中存在误差累积并传递到下一次迭代中，而积分方程法不存在误差的累积和传递。基于这些优点，前人对积分方程法进行了很多的研究。T M Habashy等［1]提出用局部非线性近似方法，对电磁场问题进行研究，但这种方法运算复杂不适于实际应用推广。Zhdanov等［2]受到TM Habashy的局部非线性近似方法的启发，在遇电磁场散射场问题时提出了拟线性近似方法求解散射场的积分方程。这种方法通过假设异常电场Ea(r)与正常电场E0(r)之间是由电反射张量联系起来的拟线性关系，即:。简化了电磁散射的积分方程，从而可以提高计算速度，电反射张量由最优化的方法求出。Zhdanov［3]在2000年将拟线性近似方法应用于电磁场反演，并用来反演美国新墨西哥州的CSAMT数据。由于拟线性近似时仍无法避开解线性代数方程组，因此Zhdanov经过研究后，提出假设电反射张量在异常体内为缓变函数，由一种相对简单的替代方法确定，这种方法称为拟解析近似方法［4]，并提出了拟解析近似序列。孙建国［5、6]在通过电磁场中的拟线性近似方法和拟解析方法研究的基础上，先后提出将拟线性近似方法和拟解析近似方法的应用，扩展到直流电场模拟及声波散射模拟。孙建国［7～9]分别对2.5维直流电阻率正演和地球物理反演中拟线性近似方法的应用进行了讨论，接下来又研究了稳定电流场的电位反射函数。孙建国［10～12]2004年对稳定电流场中的拟线性近似方法进行了研究，给出了直流电位场数值模拟的拟解析方法。在2005年孙建国［13、14]研究了直流电场中的电反射张量，给出直流电场中的拟线性近似方法和拟解析近似方法的理论公式，并对电反射张量进行了详细的分析，对稳定电流场拟解析近似方法也进行精度分析。在2006年，孙建国［15]又对稳定电流场拟解析近似方法进行了数值评价。在2008年，张金会［17]用拟解析近似方法对均匀场中的异常球体进行了研究，并对拟解析近似方法的精度进行了分析和研究。