协同克立格法在广西林旺金矿化探数据处理中的应用

徐银河，孙春岩，竺玮煌，赵志涛，杨 奎，刘 钧

(中国地质大学 工程技术学院，北京100083)

协同克立格法在广西林旺金矿化探数据处理中的应用

徐银河，孙春岩，竺玮煌，赵志涛，杨 奎，刘 钧

(中国地质大学 工程技术学院，北京100083)

协同克立格法，同时兼具化探数据多元性及克立格法表征空间属性的特点。考虑到地质变量两个以上的空间属性，在化探数据处理中运用协同克立格法，可以进一步提高估计精度。运用协同克立格法对广西林旺矿区中金元素成矿进行预测，经相关性分析显示，在矿区中元素的基本组合是Au、Ag、As、Hg，协同克立格插值以Au为主要变量，伴生元素Ag、As、Hg为次要变量。把插值计算后的结果与传统多元统计方法和普通克立格法的计算结果进行比较，结果协同克立格法得到的估值误差较小，预测精度较高，在成矿元素的预测中具有一定程度的优越性。

协同克立格法;相关分析;变差函数;估计精度

0 前言

在金属矿化探数据处理中，传统的多元统计分析处理实际问题效果比较好，但其缺点是随机理论的一些假设前提，在地质上难以满足，并且不能分析地质变量所特有的空间属性。在地质统计学中，最重要的方法，即克立格法是一种线性、无偏、最小估计方差的估计方法。它是一种既能保持概率统计方法的有效性，又更切合地质变量特点的方法途径。克立格法从单一变量出发的插值计算，避免了系统误差，可以做到最优的估计。由于化探数据多元性的特点，使得运用协同克立格法可以做到对多个相关变量的克立格估值，提高预测精度。作者利用协同克立格法对广西林旺金矿数据资料进行了分析，与传统多元统计及普通克立格法的计算结果比较，对计算得到的误差精度进行了分析对比［1、2]。

1 矿区原生晕地球化学特征

本区矿体主要赋存于三叠系百逢组，少量分布于板纳组的碎屑岩挤压、揉皱带中。矿体多成似层状，脉状、透镜状分布于揉皱强烈的砂岩、泥岩断裂、节理、劈理裂隙带中，以及褶皱轴部岩层受挤压的裂隙带中。

在矿区内，褶皱和断裂都较发育，几乎所有成矿成晕元素都是沿北西向东翼压扭性断裂分布。其中，尤以Au、Ag、As、Hg表现最为明显，说明了北西方向控矿构造的存在，Au异常受控矿构造的控制。土壤与岩石中的Mo、W、Bi，可能指示矿体线剥蚀程度，而Ni、Co的出现，可能是矿体剥蚀更深的指示。

至今，林旺矿区氧化矿的主要矿段已基本采完，而原生矿尚未完全探明和开采利用，故对深部原生矿进一步的勘查，对矿区今后的发展具有重大的意义。

矿床原生晕最重要的特点之一，是它具有分带性。造成分带的原因，主要是成矿溶液在运移过程中，其组份浓度的不断变化，各种元素化学活动性及析出顺序的不同，往往导致了同种指示元素的含量及不同指示元素的含量，在空间上有规律的变化，这种现象被称为原生晕的分带性。在以往的工作中，已应用原苏联学者格里戈亮计算原生晕中元素分带序列的方法，对矿山矿段的部份原生晕样品，计算了元素的分带序列，获得矿山矿段的元素分带序列为:

(1)前缘(上部)元素组合(As－Sb－Hg－Au)。

(2)近矿(中部)元素组合(Hg－W－Au－Ag－Mo)。

(3)尾部(下部)元素组合(Cu－Co－Bi－Ni－Zn－Pb)。

可以看到，不同指示元素在空间上是按一定的规律变化分布的［3]。

原生晕中元素的分带性，指示了元素的空间变化规律，所以在化探数据处理中，需要考虑到元素的空间属性。而传统的多元统计方法基于随机理论，不能够完整地表达出地质变量的空间相关性。而协同克立格法，既能反映变量的空间属性，同时也考虑了元素多元性的特点，更加贴合地质变量的实际情况。

2 协同克立格法

克立格法是以变差函数理论和结构分析为基础，对区域化变量进行线性、无偏、最优内插估计的方法。它是从研究矿产储量计算及其误差估计问题而产生和发展起来的，在化探数据处理中，应用克立格法考虑了化探异常的空间属性，可以避免系统误差，同时提高估计精度。

化探数据具有多元性的特点，而普通克立格法研究区域化变量只从单一变量出发，不能够很好地满足化探数据处理的需求。用协同克立格法进行分析评价，可以很好地兼顾克立格法与数据多元性的特点。协同克立格法是把区域化变量的最佳估值方法，从单一属性发展到二个以上的协同区域化属性。协同克立格法在插值时，用一个或更多的次要变量，这些次要变量与主要变量有相关关系。变量之间的相关关系，能用于提高主要变量的预测精度［2、4]。

3 研究区元素统计特征

通过统计分析后可以运用变差函数建立模型，进而用克立格法估值。在计算变差函数之前，必须对样品数据进行分析和处理。样品特异值(即样品中的特高含量值)的存在，将严重影响变异函数的结构性。在对原始数据进行统计分析前，将含量异常的特异值剔除掉，在得到的数据中对Au元素含量进行对数转化后服从对数正态分布，见图1，所以可以用克立格法进行插值估计。

图1 林旺金矿Au含量对数统计直方图Fig．1 Logarithmic histogram of gold element

首先，对林旺金矿主要的十三种元素进行统计分析，其元素含量的相关矩阵见下页表1。通过计算相关系数，可以得出:

(1)主成矿元素Au与Ag、As、W、Hg元素在含量变化上呈正相关特性。

(2)Au与Sb、Mo元素在含量变化上呈相对微弱的正相关特性。

(3)Au与Bi、Co、Cu、Ni、Pb、Zn元素呈负相关特性。

Au元素的异常组合，可以通过正交旋转主因子解进一步确定，见下页表2。从表2中可以看出，Au元素与Ag、As和Hg元素关系密切［5]。

4 结果分析

4．1 建立和计算变差函数模型

协同克立格法是研究一个变量取样值时，借助其它与之相关的变量样品信息，来提高对该变量的估计精度。协同克立格法利用了更多的样品信息，比较普通克立格法而言，计算量更大一些。通过统计分析得出，Au元素与Ag、As和Hg元素关系密切，进而运用协同克立格法对其估值。

统计分析的结果表明，Au元素的含量服从对数正态分布，所以在计算变差函数之前，要对Au元素的含量数据进行对数转换。在统计分析的基础上，首先要建立变差函数模型，变差函数的重要性在于获得了表征区域化变量空间特性的三个参数，即变程、块金效应、基台值，这三个参数可用于求取克立格计算时所需的权系数，所以变差函数能较好地反映成矿异常的空间结构性和随机性。

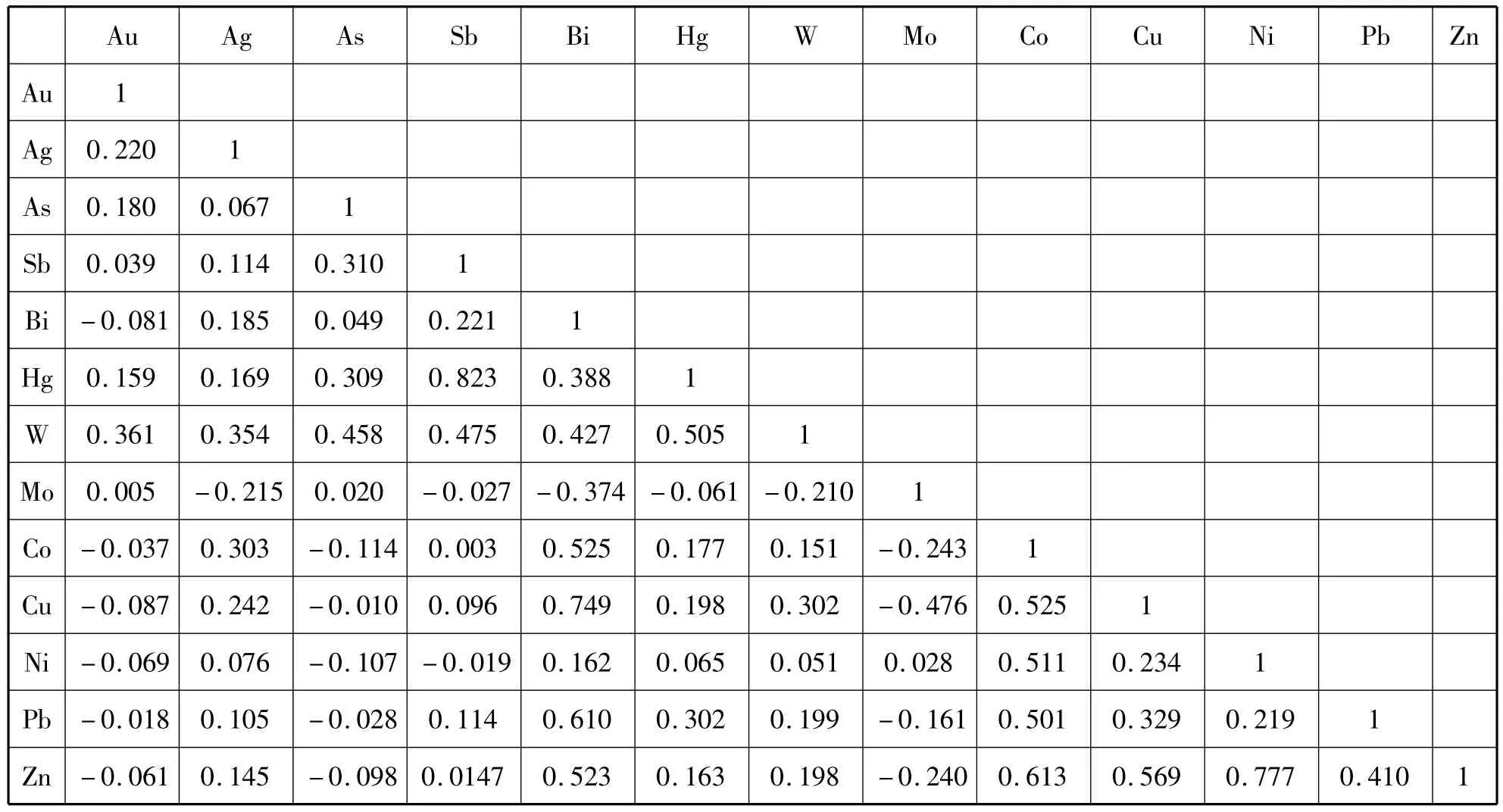
表1 林旺矿区十三种元素含量的相关矩阵Tab．1 Correlation matrix of 13 elements

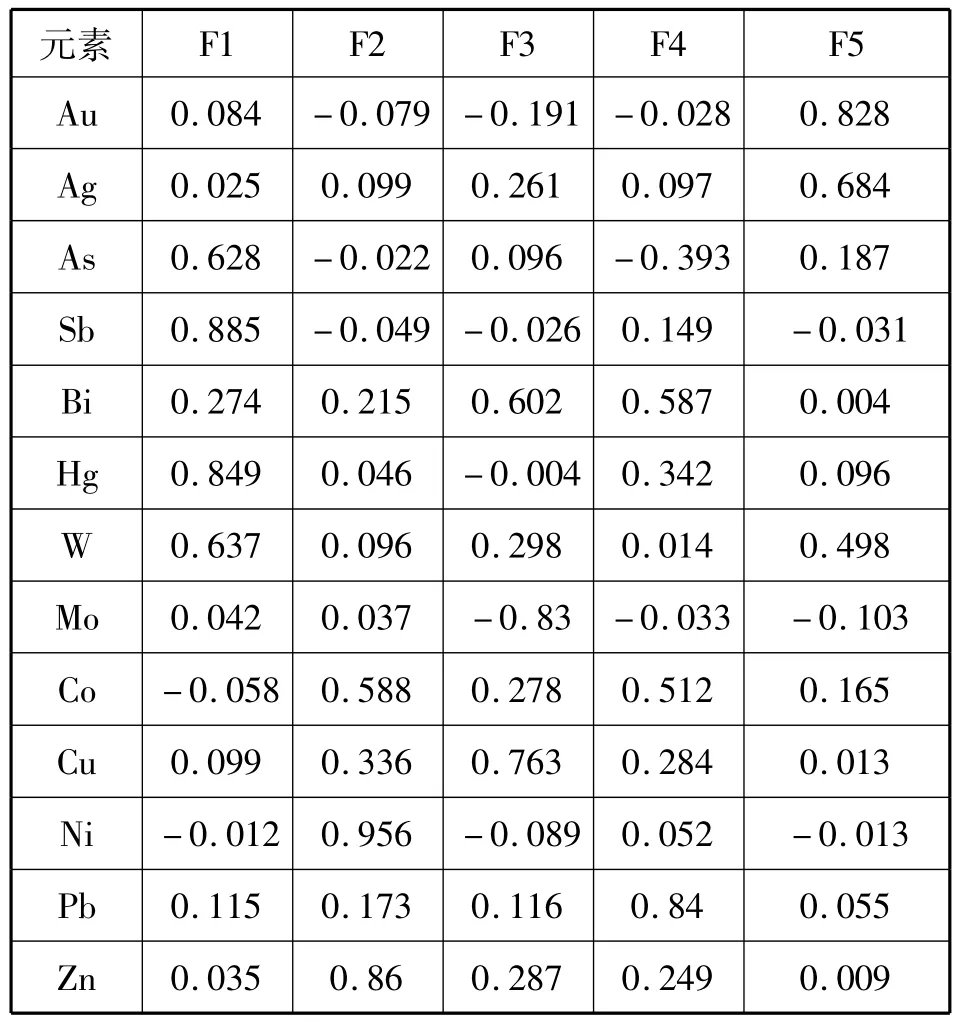
表2 正交旋转主因子矩阵Tab．2 Rotated componentmatrix

协同克立格变差函数如下:

协同克立格法的任务，是应用估计领域内的有效数据，来估计中心点在x0的待估域V(x0)上，变量k0的平均值Zvk0的估计量

在插值中，要考虑到领域样品的搜索形式及搜索半径的选择，通常的搜索方式有椭球体和球体二种。由于克立格法的适用条件需满足平稳性假设与内蕴假设条件，所以选择用于区域化变量在空间平稳分布的球状模型。这就要求在应用时，对所研究的矿床有一定了解，取样数据点不能太少［6]。

在分析变差函数特点的基础上，确定用球状模型进行理论变差函数拟合。变差函数曲线反映了一个采样点与其相邻采样点的空间关系，对异常采样点具有很好的探测作用。在图2(见下页)中，点图为实验变差函数，通过计算样品值的变差函数，得到了理论变差函数。在图2中的曲线，即为理论变差函数曲线。从图2中可以看出，实验变差函数与理论变差函数曲线拟合情况良好。

Au元素样品点分布不具有趋势，拟合的变差函数不具有几何各向异性，即各个方向的变差函数均具有相同的基台值和变程。当采样点间的距离增大时，变异函数从初始的块金值达到一个相对稳定的常数时，该常数值称为基台值。当变差函数值超过基台值时，即函数值不随采样点间隔距离而改变时，空间相关性不存在。当变差函数的取值由初始的块金值达到基台值时，采样点的间隔距离被称为变程。变程表示在某种观测尺度下，空间相关性的作用范围，其大小受观测尺度的限定。块金值就是在二采样点非常接近时，它们的变差函数值不为0，即存在块金值。球状模型的变程是0．233 833，偏基台值是0．518 81，块金值是1.161 9，滞后距是0．040 936，滞后数是12。

4．2 变差函数的交叉验证

用克立格法估值时，需要将原始数据分成二部份，即计算数据和检验数据。其原理是用选定的理论变差函数的参数，对已知数据利用其周围的数据进行克立格估值，将所得的这套估计值与原始值进行比较，并对其结果进行统计分析。良好的检验结果将是二套数据的均值之差很小，方差也很小，以及有良好的正相关性，从而判断参数的正确性。

验证之后的数据见表3和图3。

从表3可以看出，标准平均值非常接近于0，均方根预测误差也很小，平均标准误差与均方根预测误差非常接近，均符合最优变差函数模型的要求。可以得出结论:计算变差函数模型是最优的;对样品含量的估计是无偏的;满足区域化变量的内蕴假设;验证该变差函数的模拟是正确的。

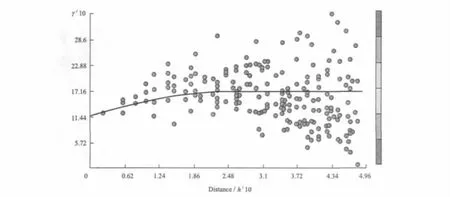
图2 实验变差函数与理论变差函数拟合图Fig．2 Experimental variogram and theoretic variogram

表3 交叉验证模型参数Tab．3 Parameters of cross validation

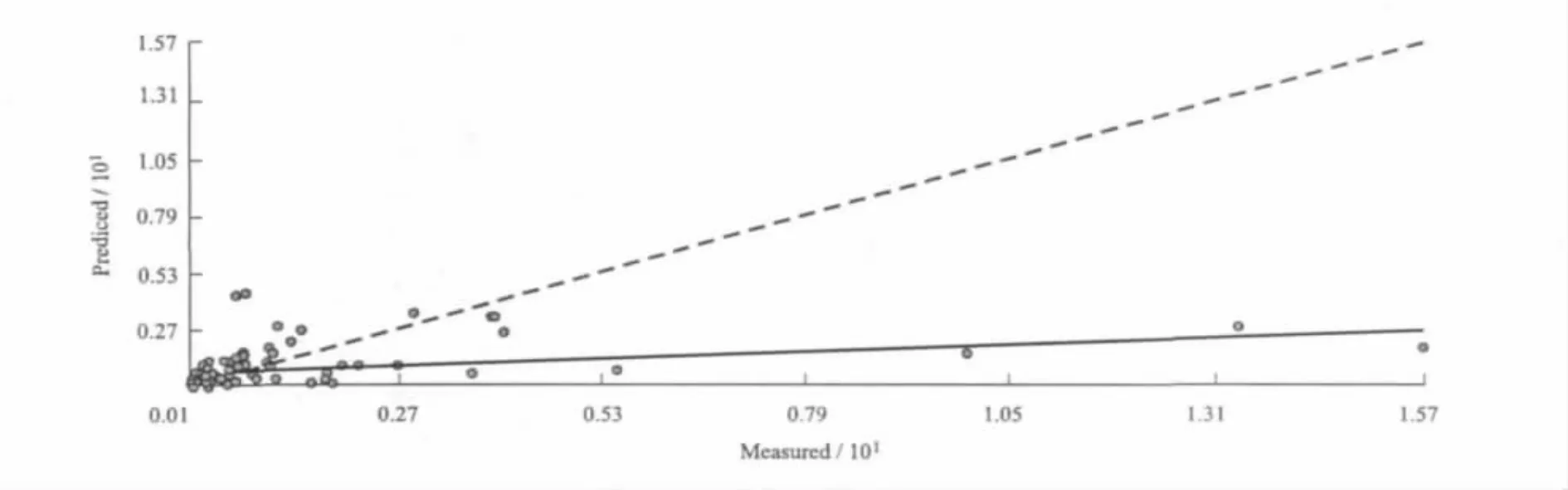
图3 交叉验证的预测图Fig．3 Cross validation prediction

同时，利用普通克立格法对矿区化探数据进行分析评价，从表4可以看到，用协同克立格法对原始数据进行估值时所得到的预测误差，要比普通克立格法得到的预测误差减少11.11%，标准误差减少23.38%。由此可见，协同克立格法与普通克立格法相比，在一定程度上，协同克立格法是较为优越的，这对于提高地质统计学的预测精度，起到了一定的作用。但该方法唯一缺点就是计算量比较大，不过可以通过先进的软件来解决。

通过对变差函数模型的计算以及得到的精度，可以对林旺矿区的Au元素进行估计，得到的预测图见图4［4、7]。

图4 林旺矿区Au元素异常预测图(1∶10 000，ArcGIS)Fig．4 Gold element abnormity predication

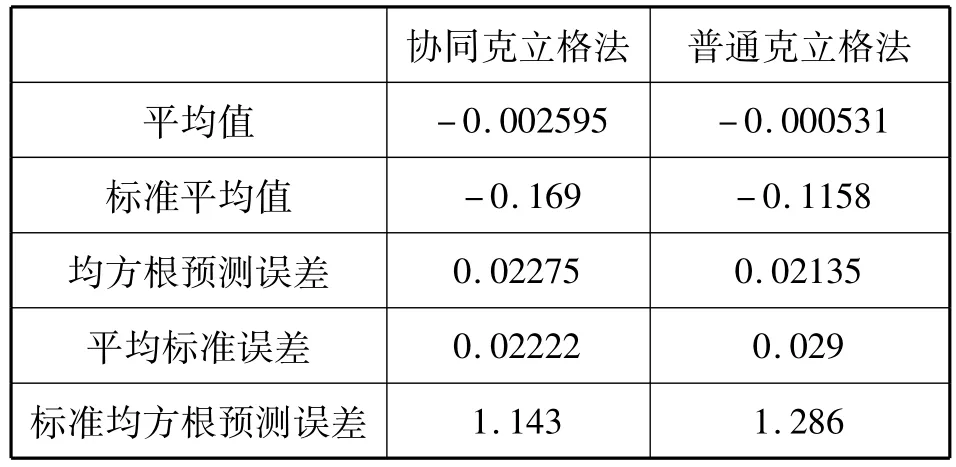
表4 Au元素协同克立格法与普通克立格法交叉验证结果比较Tab．4 Cokriging and normal kriging of gold element in cross validation

5 讨论

(1)协同克立格法结合了化探数据处理的多元性，以及克立格法反映空间属性的特点，与传统多元统计分析相比，较能够反映出地质上区域化变量的空间特征。

(2)在化探数据处理中，运用协同克立格法估值，在一定程度上提高了预测的精度，得到了较为精确的估计精度。与普通克立格法相比较，协同克立格满足了多变量估值的要求，更加符合化探数据统计的要求，缺点就是计算量比较大，需要运用先进的软件来处理。

(3)运用协同克立格法研究区域化变量时，要满足平稳假设和内蕴假设条件，所以需要对所研究矿床有一定的了解，取样数据点不能太少。

［1]余先川，王世称，王桂安．稳健协同克里格因子分析及其在化探中的应用［J]．地球科学—中国地质大学学报，1998，23(2):1．

［2]王仁铎，胡光道．线性地质统计学［M]．武汉:武汉地质学院教材科，1984．

［3]吴锡生．广西乐业县林旺金矿勘查地球化学深部找矿工作报告［D]．北京，2009．

［4]伍伟，秦德先，胡志军，等．地质统计学在曼家寨锡锌多金属矿床中的应用［J]．有色金属，2008，60(2):2．

［5]叶水盛，刘光盛，马生忠．克立格方法在区域化探数据处理中的应用［J]．长春科技大学学报，2000，30(2):1．

［6]杨建宇，秦德先，康泽宁等．地质统计学在北衙金矿的应用［J]．矿业研究与发展，2006，26(2):3．

［7]汤国安，杨昕．ArcGIS地理信息系统空间分析实验教程［M]．北京:科学出版社，2006．

P 632

A

1001—1749(2011)02—0179—05

广西国土资源厅普查项目(4500000330364)

2010－09－03改回日期:2010－12－08

徐银河(1985－)，女，硕士，主要从事基于GIS的数学地质方法在矿产资源评价中的应用。