VTI介质隐式有限差分平面波偏移

韩 利，韩立国，崔 杰，巩向博

(吉林大学地球探测科学与技术学院，长春130026)

VTI介质隐式有限差分平面波偏移

韩 利，韩立国，崔 杰，巩向博

(吉林大学地球探测科学与技术学院，长春130026)

这里研究了VTI(Vertical Transverse Isotropy)介质隐式有限差分(IFD)波场外推算子和VTI介质平面波偏移。在文中设计了VTI介质IFD波场外推算子，将Taylor分析法求得的差分系数，作为初始解，用非线性优化方法迭代求得算子系数。将设计的外推算子频散曲线和偏移脉冲响应与理论解进行了对比分析，验证出外推算子有较高的精度。从各向同性介质平面波偏移理论出发，结合VTI介质IFD波场外推算子，将平面波偏移推广到VTI介质中。对Hess VTI标准模型拟合数据进行偏移，偏移结果验证了平面波偏移在VTI介质中的有效性，以及在加强特定陡倾界面成像方面的优势。并且，与常规VTI介质叠前深度偏移相比，VTI介质平面波偏移在保证成像质量的前提下，大大减少了计算量，为各向异性偏移成像研究提供了新的技术思路。

平面波偏;VTI介质偏移;各向异性偏移;VTI介质波场外推;隐式有限差分算子

0 前言

波动方程叠前深度偏移，可以克服Kirchhoff偏移多路径和高频假设的限制，能在横向变速强烈的复杂地区产生更好的成像。但是，波动方程叠前偏移耗时很大。为此，许多学者研究了平面波偏移在减少计算量，提高波动方程偏移效率上的潜力。Berkhout［1]提出面炮偏移技术;张叔伦等［2]实现了傅立叶有限差分平面波偏移;Zhang等［3]实现3D延迟放炮偏移;Stoffa等［4]对共检波点道集和共炮道集分别作平面波偏移，再叠加以提高成像精度;崔兴福等［5]利用平面波偏移进行了分角度成像和AVA分析;叶月明等［6]研究了起伏地表下的平面波偏移;Shan等［7]提出倾斜坐标系下平面波偏移以提高高角度成像准确度;韩利［8]实现对称非稳态相移法平面波偏移。平面波偏移还可以自然地产生共角度道集，用来进行速度更新［3]。

但这些关于平面波偏移的研究，基本都是在各向同性介质下，没有考虑各向异性介质情况。而各向异性在石油勘探中普遍存在，如果地下介质存在较强各向异性而在偏移时被忽略，反射波将不能被正确归位［9]，甚至扭曲构造形态，这对地层连续性和横向构造均有较大影响［10、11]。VTI模型可以有效地刻画地下许多沉积地质模型，常被用来进行各向异性偏移研究。

与各向同性介质相比在VTI介质中波的频散关系要复杂些，因为其传播速度依赖于相位角。所以，在VTI介质波场外推经常使用相移加内插［12]或显性卷积方法［13、14]，因为复杂的频散关系并不增加这些方法的复杂性。但是对于相移加内插法，需要大量的参考波场。显性卷积方法在各向同性下都很难保证稳定性，而且需要很长的卷积滤波算子以保证精度。作者在本文选用能很好处理横向变速问题的隐式有限差分(Implicit Finite Difference:IFD)算法［15]。Ristow等［16]基于弱各向异性假设和Taylor分析将其拓展到VTI介质。为了改善精度，Liu等［17]在有限差分后加入了相位改正算子。Shan［18、19]提出了优化的方法，将非线性问题降解为线性优化问题，再利用线性优化解出的系数求解差分系数。作者在本文延用Shan避开弱各向异性假设及优化的思想，不同的是作者直接建立非线性优化问题，并将Taylor序列展开法求得的系数作为初始解，直接使用非线性最小二乘求解差分系数，得到VTI介质中IFD外推算子。

首先，作者介绍了各向同性介质下的平面波偏移理论，接着阐述了在VTI介质中IFD算子系数设计，结合二者，将平面波偏移推广到VTI介质中。将设计的外推算子频散曲线和偏移脉冲响应，分别与理论解做了对比分析，应用Hess VTI标准模型数据来验证平面波偏移的有效性，并展示了平面波偏移在加强陡倾目标界面成像方面的优势。

1 各向同性介质平面波偏移

常规叠前偏移是通过对单个炮集进行独立偏移得到单炮成像，并通过叠加所有的单炮成像得到整个地下成像。波动方程单炮偏移过程需要两步:①将震源波场和接收波场从地表外推到地下所有的深度;②在每个深度通过对震源波场和接收波场，应用成像条件(如做互相关)得到成像。

炮集记录可以合成一个新的数据体，来表征一个现实中没有进行的物理实验。这种数据合成方法的一个重要的例子，就是组合炮集记录建立平面波震源记录。在数学上，可以通过对共检波点道集进行倾斜叠加(线性Radon变换)来实现:

其中R=R(sx，x，z，ω)是接收波场;sx是震源位置;psx是相应于sx的射线参数;rx是地表检波器位置。相应的地表平面波震源波场为:

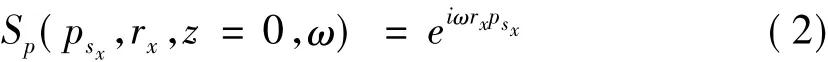
和常规波动方程炮域偏移一样，典型的平面波偏移也需要二步:①将震源波场Sp和接收波场Rp，分别用单程波动方程独立地外推到地下所有深度点;②含有射线参数Psx的平面波成像，通过对震源波场和用圆频率ω加权了的检波波场作互相关实现:

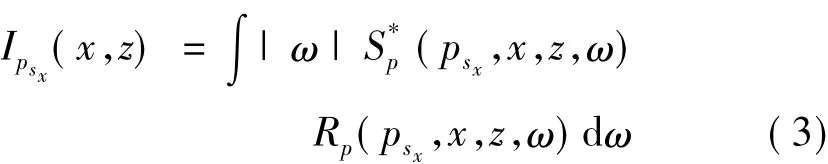
其中S*p是震源波场Sp的复共轭。

整个图像通过叠加所有Psx值的平面波成像得到:

因为倾斜叠加和偏移都是线性算子，在连续情况下，平面波偏移与传统的炮剖面偏移效果一样［2]。在实际离散形式下，需要有足够数量的P值使二种成像等同。Zhang等讨论了在平面波偏移方法实际应用中需要的共P剖面数量Np及分量采样步长Δp:

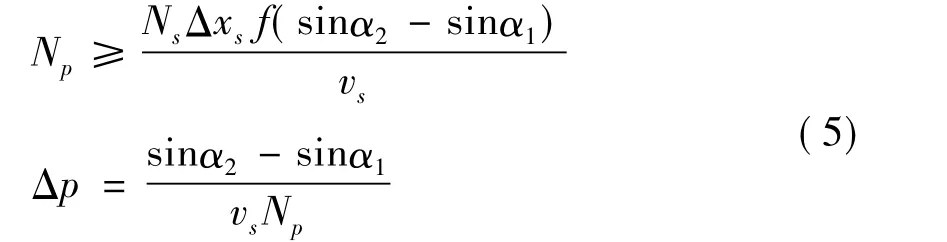
其中f=ω/2π，Ns为一个共检波道集中的炮数;Δxs为炮间距，所以NsΔxs为一个共检波道集的长度;入射角α1≤αs≤α2;vs为地表速度。

2 VTI介质中IFD算子设计

2.1 VTI介质中的频散关系

VTI介质有一个竖向旋转对称轴，相速度依赖于介质的竖向速度及相速度的传播角。在VTI介质中，qP－波和qSV－波的相速度，可以用Thomsen符号表示(Tsvankin，1996):

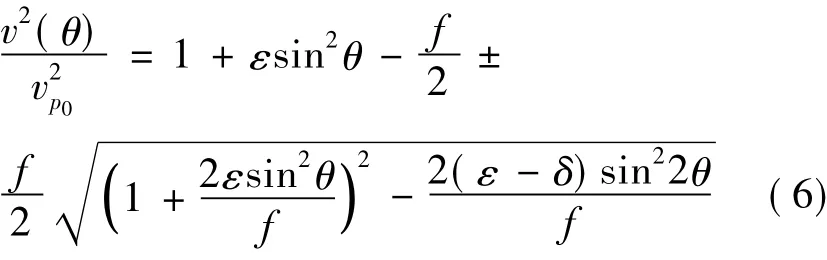
其中 θ为波的相位角，即波传播方向与竖向轴之间的夹角;f=1－(vs0/vp0)2;vp0和vs0分别为qP－波和qSV－波在竖向方向的速度。

在式(6)中，当根号前符号为正时，v(θ)为qP－波的相速度，为负时，v(θ)为qSV－波的相速度。

通过式(6)及相位角θ和波数的关系，可以得到VTI介质中的频散关系［18]:

其中sz=kzvp0/ω，系数d0、d2和d4分别为:4

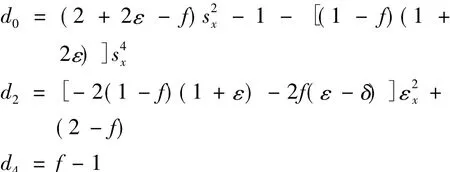
其中sx=kxvp0/ω。

VTI介质中的频散关系式(7)是一个有四个解的四次方程，其中二个解代表上行/下行qP－波，另外二解代表上行/下行qSV－波。我们只考虑qP－波的外推。

2.2 IFD算子系数设计

在实际应用中，假设在qSV－波速比qP－波速度小得多时有f≈1，Shan［18、19]根据这个假设，从式(7)中简化qP－波的频散关系为:

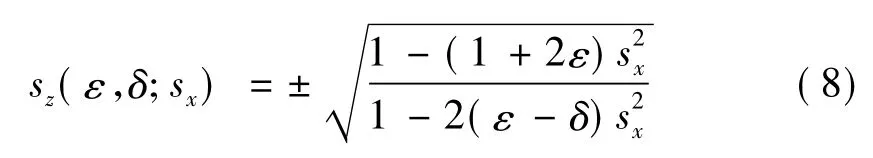
该频散关系虽然有一点假设，但不受弱各向异性的限制。对式(8)进行逆Fourier变换，得到VTI介质下的上行和下行单程声波方程式(9)(用代替sz，用代替s2x)。

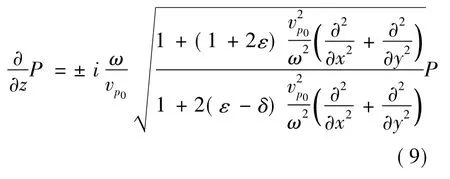
为了设计式(9)的IFD模式，需要用一个加权函数式(10)近似sz:

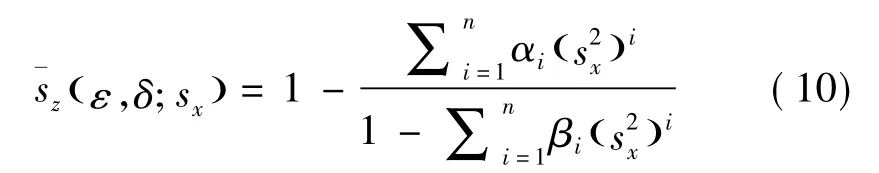
这里加权函数系数αi和βi也可以通过Pade展开得到。Shan提出用优化的方法求解，首先建立加权优化函数，并将其化为线性最小二乘可解的优化函数，在求得优化系数后进一步分裂为式(11)的形式:

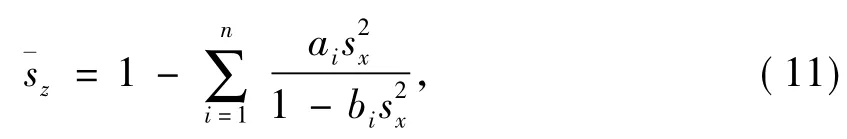
其中 系数ai和bi通过αi和βi，i=1、…、n计算得到。

作者直接从式(8)设计加权函数式(11)，建立如式(12)的优化问题。

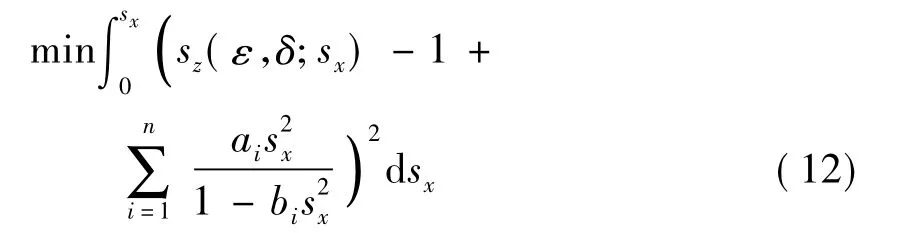
式(12)是一个非线性优化问题，需要用非线性最小二乘法解。作者采用高斯～牛顿迭代法解［23]，利用Taylor展开分析算出一组ai和bi，i=1、…、n作为迭代的初始解，这样就可以减少迭代的计算量。在算出系数ai和bi后，VTI介质中的IFD波场外推和各向同性下相同。

图1是当各向异性参数为ε=0.2、δ=0.15时，对几种频散关系与VTI介质频散关系解析解进行的比较。在图1中，曲线“True”是由式(8)得到的真实频散关系;曲线“Isotropic”是不考虑各向异性影响时的频散关系;曲线“Taylor－weak”是由D Ristow等［16]方法解出的频散关系。可以看出，这种近似在低相位角时拟合的很好，而在高相位角时有些偏差;曲线“Optimization”为用本文建立的优化式(12)解出的频散关系，由图1中可以看出，这种近似与真实频散关系几乎完全匹配，精度很高。几种近似方法在各向异性参数为ε=0.2、δ=0.15时，对应的四阶优化系数(n=2)见表1。用同样的办法也可以拟合更高阶差分系数。

图1 频散关系曲线比较(ε=0．2，δ=0．15)Fig.1 Dispersion relation comparison withε=0．2，δ=0．15

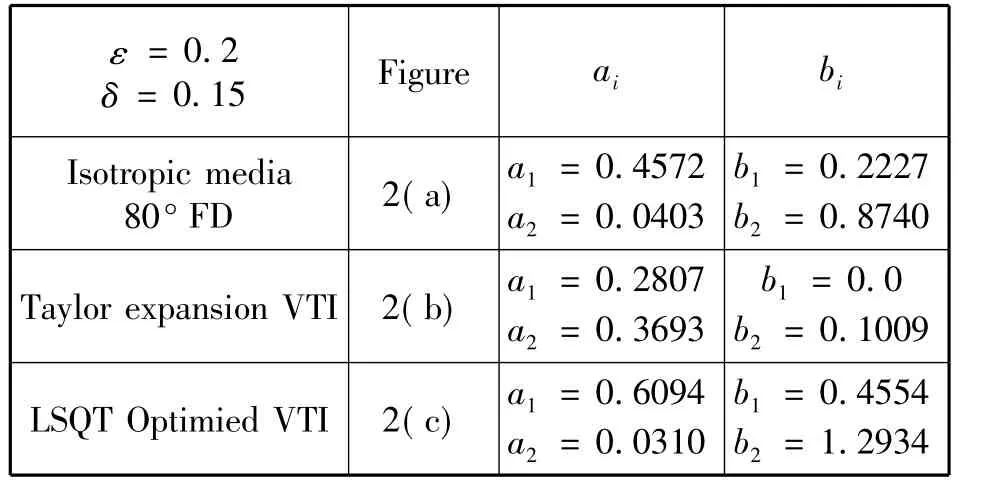
表1 ε=0．2、δ=0．15几种方法求出的四阶(n=2)优化系数Tab.1 The coefficients of different approximately operators withε=0．2，δ=0．15

图2(见下页)是在各向异性参数为ε=0.2、δ=0.15，速度vp0=2 000 m/s，时间t=0.8 s时，几种方法的偏移脉冲响应。其中，深色线是根据式(6)及速度时间等参数算出的理论曲线(理论曲线单程按t=0.4 s计算)。图2(a)是各向同性IFD 80°差分算子对各向异性介质下的脉冲响应，从图2(a)中可以明显看出，忽略各向异性将会带来很大误差，尤其是在横向方向误差较大;图2(b)是由Taylor展开法计算得到的差分系数构建差分算子得到的脉冲响应，从图2(b)中可以看出，脉冲响应与理论曲线基本吻合，但在在大角度时失真。图2(c)为解本文构建的非线性优化问题式(12)得到的差分系数得到的偏移脉冲响应，与理论曲线匹配的非常好，这就证明本文使用直接解非线性优化问题得到的差分系数非常准确。

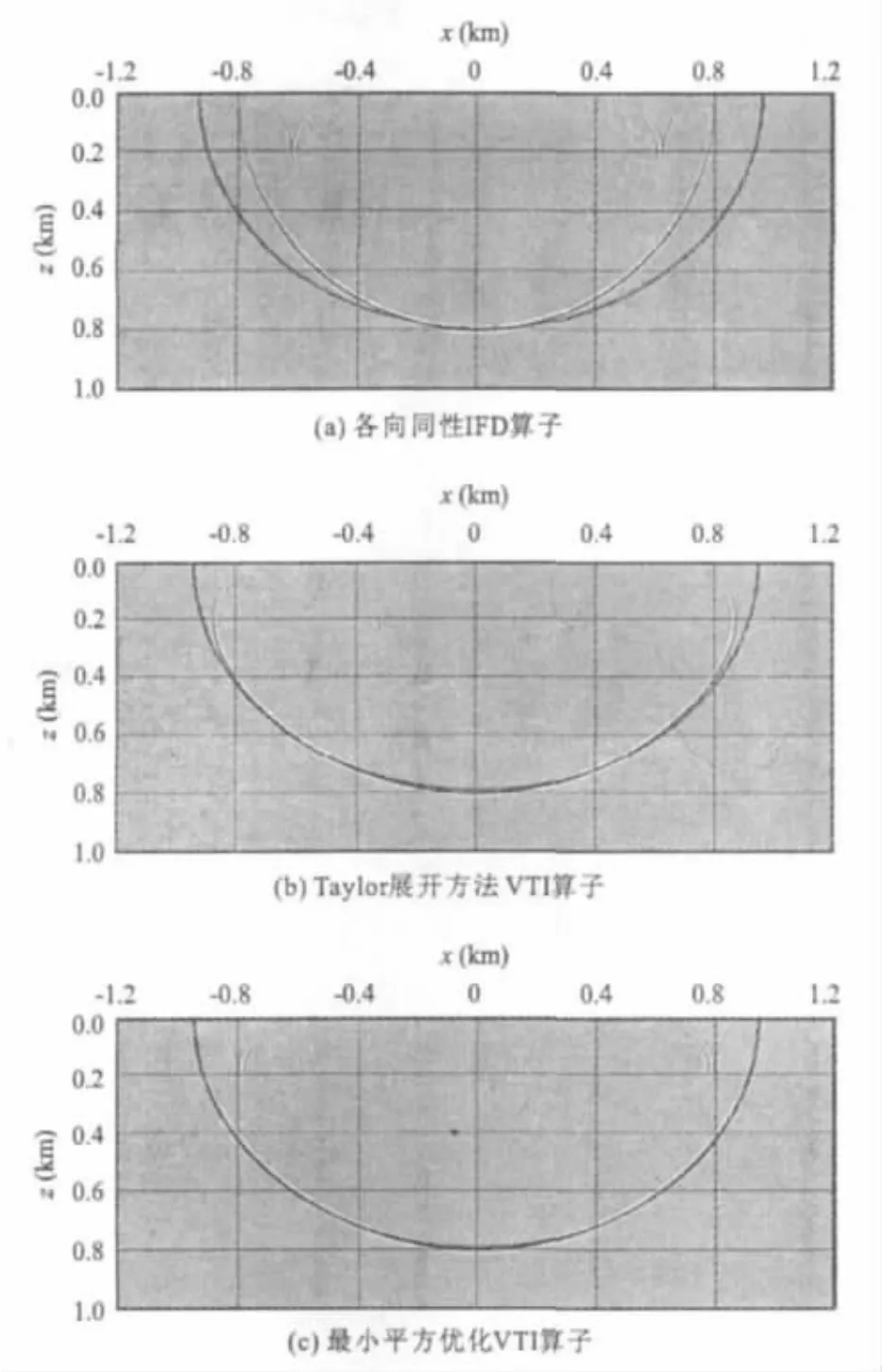
图2 几种方法的脉冲响应，VTI介质参数:vp0=2 000 m/s，ε=0．2，δ=0．15，t=0．8 sFig.2 Impulse response of a tilted VTImedia with vp0=2 000 m/s，ε=0．2，δ=0．15，t=0．8s

3 VTI介质平面波偏移

在各向同性介质中，平面波偏移通过解上行/下行波方程，再利用式(3)和式(4)的成像过程成像。在VTI介质中，平面波的合成过程和成像物理过程是不变的，但应用的波传播方程不一样了。利用上面构建的VTI介质中IFD外推算子，来解VTI介质中声波方程(9)。VTI介质中波场外推算子的精度越高，成像越精确，但算子精度越高需要求解的优化问题计算量就越大，这就使得各向异性偏移计算量一般要高于各向同性情况。应用平面波偏移，较常规各向异性偏移大大减少了偏移的计算量。

另外，在常规VTI介质偏移中，由于偏移孔径的限制，单炮偏移只能加强很窄孔径内的成像，而应用平面波偏移，每一个P面的成像孔径是整个测线，参数P又与地下界面倾角有一定的关系，根据这一原理，对特定P参数成像，可加强地下特定角度界面的成像。

4 模拟算例

理论实验模型数据采用Hess VTI标准模型，拟合数据由Amerada Hess提供，该数据是用Standford University SEP实验室的有限差分正演软件正演的，不包含与地表有关的多次波。数据由720个炮集组成，网格间距d x=d z=6.096 m，炮间距30.48 m，道间距12.192 m，最小偏移距0 m，最大偏移距7 985.8 m，采样时长为7.992 s，采样间隔为6 ms。模型如图3所示。

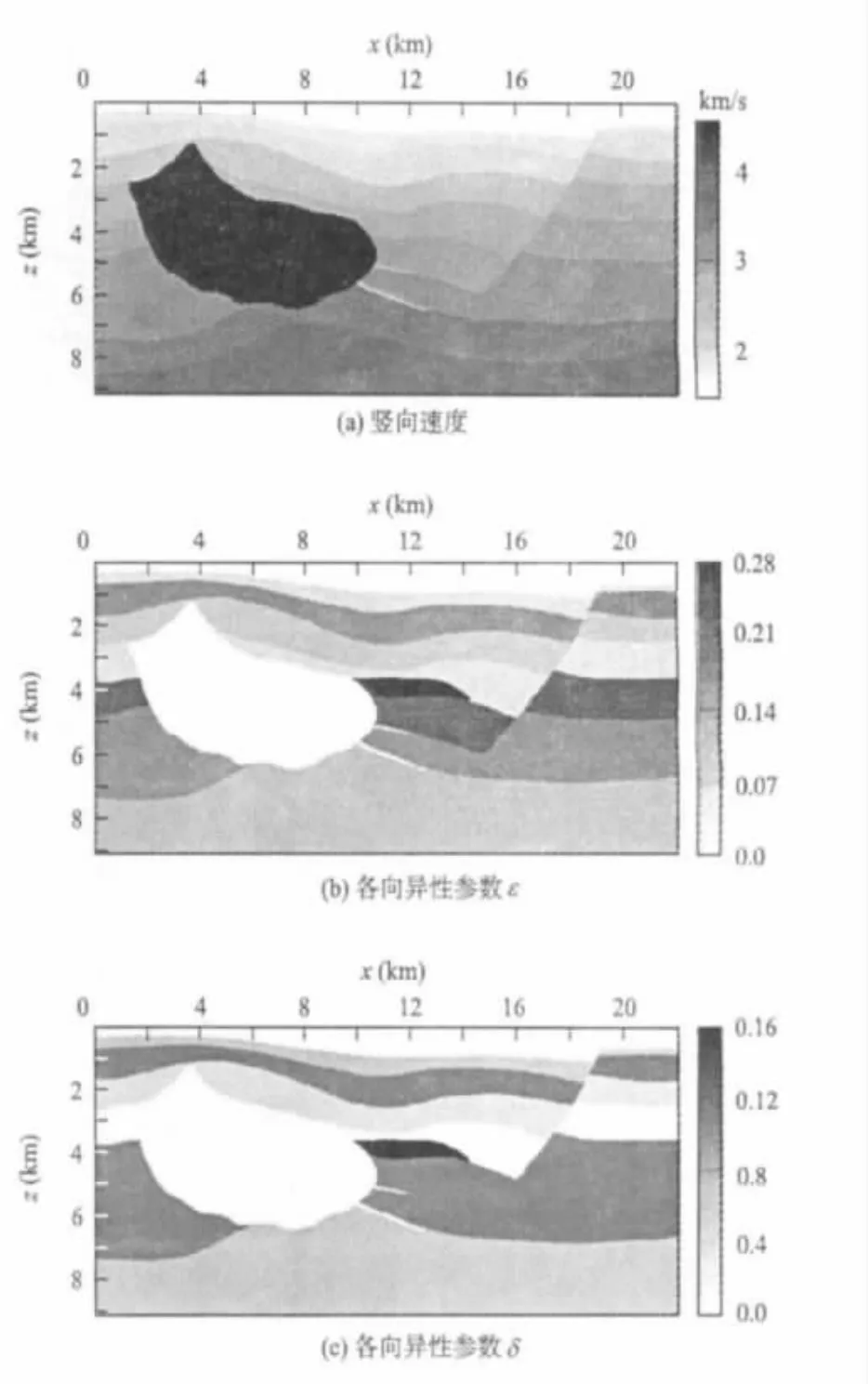
图3 Hess VTI标准模型Fig.3 Hess VTImodel

图4是应用各向同性介质下有限差分做的叠前深度偏移。

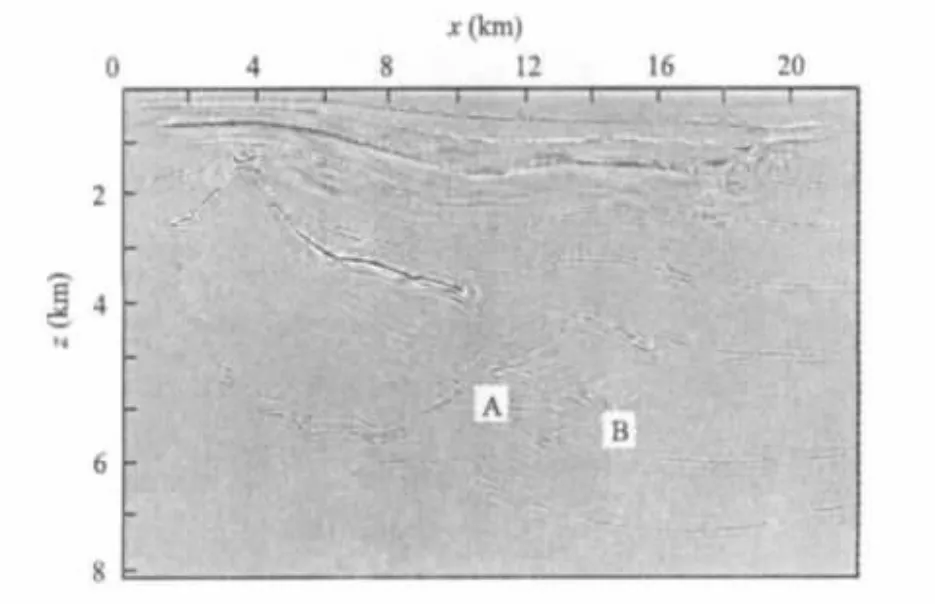
图4 各向同性波动方程IFD法偏移结果Fig.4 Imaging obtained by Isotropic IFD operator

图5是使用式(12)构造的VTI介质中波场外推算子做的常规炮剖面法VTI介质叠前深度偏移。

对比图4与图5，从A、B二处可以看出，如果地下是各向异性介质，用各向同性的方程偏移不能将地质体正确归位。

根据方程(5)，NsΔxs取最大偏移距长度为7 986 m，f取45 Hz，α 取 正、负30°，vs取1 500 m/s，则得到 Δp=2.8μs/m，Np=240。如果NsΔxs取小一点还可以取更少的P面。图6是用240个P面叠加得到的VTI介质中平面波偏移结果，与图5比较，平面波偏移用小于常规偏移几倍的计算量得到与之相同质量的成像。

从图5和图6可以看出，不管是常规炮剖面偏移方法还是平面波偏移方法，在盐体左腰处陡界面成像质量都较差。因此，通过偏移加强陡倾界面成像意义重大。

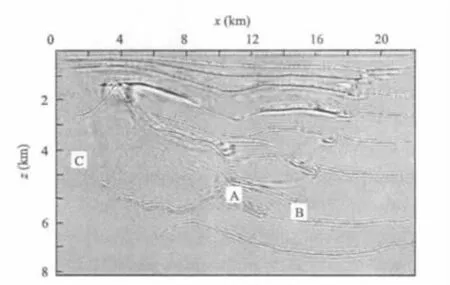
图5 VTI介质中传统波动方程IFD偏移结果Fig.5 Imaging obtained by conventional VTImedia shotprofilemethod wave equationmigration

图6 VTI介质中平面波IFD法偏移结果Fig.6 Imaging obtained by VTImedia plane wave IFDmigration

图7(见下页)是平面波偏移加强图5、图6中陡倾界面C的说明。图7(a)分别为炮点在1 738 m、3 048 m、4 816 m、6 200 m处的单炮偏移剖面，图7(b)分别为P等于 －131μs/m、－197μs/m、－262μs/m、－329μs/m时的单P偏移剖面。对比图7(a)和图7(b)可以发现，受偏移孔径限制，单炮偏移不能由某一炮或几炮对地下陡倾界面进行成像加强，而在平面波偏移中，一个单P面偏移对与之对应倾角的地下界面成像贡献较大，通过对特定的某个或几个P面成像加权，就能加强特定地下界面成像。如图7(c)为P等于300μs/m附近五个偏移剖面叠加之和，只对与之角度对应的界面成像(如界面C)。图7(d)与图7(e)分别为平面波偏移对界面C加强前后的效果。由图7可见，陡倾界面C成像明显加强。

图8(见后面)为特定陡倾界面加强后的效果，从图8中可以看出，陡倾界面C有了明显的加强。在基本没有增加计算量的情况下，在平面波偏移中，特定P面偏移改善了陡倾界面成像效果。

5 结论

作者在本文用优化方法设计了VTI介质隐式有限差分波场外推算子，将Taylor展开法求得的差分系数作为初始解，用非线性优化方法迭代求得差分算子系数。通过与VTI介质频散关系和偏移脉冲响应理论解对比分析证明，各向同性IFD算子在VTI介质偏移中会带来很大误差，尤其是在横向方向。Taylor展开法VTI介质IFD算子在低相位角时比较准，但高相位角时有一定误差。而作者在文中用优化的方法求取的VTI介质IFD算子频散曲线和偏移脉冲响应，与解析解匹配的都非常好，这也证明了设计算子的精度很高，而且不受弱各向异性假设限制。从计算量方面考虑，优化的VTI介质IFD算子比各向同性介质多出的计算量部份，为求取差分系数的部份，如果建立优化VTI差分系数库，采用表格查找系数方式，这部份时间就可忽略，而求取系数之后的计算量和各向同性下相同。

图7 平面波偏移加强特定陡倾界面成像Fig.7 Enhancing steep reflectors imaging by plane wavemigration

图8 特定P剖面加强陡倾界面C成像后的效果Fig.8 Imaging after steep reflectors enhancing by specifical Pmigration

作者在文中，结合设计的VTI介质下IFD波场外推算子，将平面波偏移理论推广到VTI介质中，并将该算法用于国际标准Hess VTI模型。拟合数据算例表明，VTI介质下平面波偏移在保证成像质量的同时，大大降低了计算量，这对各向异性偏移研究有重要意义。作者还给出了平面波偏移在加强特定陡倾界面成像方面的应用，平面波偏移用很少的计算量就能加强陡倾界面成像，这是常规炮剖面法偏移没有的一个优势。

［1]BERKHOUTA J.A real shot－record technology［J].J Seis Expl，1992，1(3):251.

［2]张叔伦，孙沛勇.基于平面波合成的傅里叶有限差分叠前深度偏移［J].石油地球物理勘探.1999，34(1):1.

［3]ZHANG Y，SUN J，NOTFORSC，et al.Delayed－shot 3D depth migration［J].Geophysics.2005，70(5):E21.

［4]STOFFA PL，SEN MK，SEIFOULLAEV RK，et al.Plane－wave depth migration［J].Geophysics.2006，71(6):S261.

［5]崔兴福，刘卫东，刘桂宝，等.平面波偏移、分角度成像与AVA道集生成［J].石油物探.2007，46(6):615.

［6]叶月明，李振春，仝兆岐，等.起伏地表条件下的合成平面波偏移及其并行实现［J].石油地球物理勘探.2007，42(06):622.

［7]SHAN G J，BIONDIB.Plane－wavemigration in tilted coordinates［J].Geophysics.2008，73(5):S185.

［8]韩利.延迟激发平面波叠前深度偏移研究［D].长春:吉林大学，2009.

［9]MARTIN D，EHINGER A，RASOLOFOSAON P.Some aspects of seismic modeling and imaging in anisotropic media using laser ultrasonics:62nd Ann.Internat.Mtg［J].Soc.Expl.Geophys.In，1992:1373.

［10]VESTRUM RW，LAWTON D C，SCHMID R.Imaging structures below dipping TI media［J].Geophysics.1999，64(4):1239.

［11]YAN L，LINES L，LAWTON D.Influence of seismic anisotropy on prestack depthmigration［J].The Leading Edge.2004，23(1):30.

［12]ROUSSEAU J.Depth migration in heterogeneous，transversely isotropic media with the phase－shift－plus－interpolation method in 67th Ann［J].Internat.Mtg.Soc.of Expl.Geophys.1997:1703.

［13]BAUMSTEIN A，ANDERSON J.Wavefield extrapolation in laterally varying VTImedia in 73rd Ann［J].73th Annual InternationalMeeting，SEG，Expanded Abstracts.2003:945.

［14]REN J，GERRARD C，MCCLEAN J，et al.Prestack wave－equation depthmigration in VTImedia［J].The Leading Edge.2005，24(6):618.

［15]CLAERBOUT JF.Imaging the Earth's interior［M].Blackwell Scientific Publications，1985.

［16]RISTOW D，RÜHL T.3－D implicit finite‐difference migration bymultiway splitting［J].Geophysics.1997，62(2):554.

［17]LIU L N，GAO H W，LIU H，et al.Wave equation depthmigration with optimum split－step Fourier method in 3－D VTImedia［J].Chinese Journal of Geophysics－Chinese Edition.2005，48(2):406.

［18]SHAN G J.Optimized implicit finite－difference and Fourier finite－differencemigrnation for VTImedia［J].Geophysics.2009，74(6):189.

［19]SHAN G.Optimized implicit finite－difference migration for VTImedia［J].In:SEG Annual Meeting;2006;New Orleans;2006:2367.

［20]Kelley CT.Iterative Methods for Optimization［M].SIAM Frontiers in Applied Mathematics，1999.

P 631.4

A

1001—1749(2011)02—0115—07

国家“973”项目(2007CB209603);国家863项目(2007AA060801)

2010－07－15改回日期:2010－10－25

韩利(1984－)，男，河北保定人，博士，主要从事地震偏移成像和反演方面的研究。