Kirchhoff叠前时间偏移关键参数分析与研究

顾 雯，王铎翰，阎建国

(1．成都理工大学 信息工程学院，四川成都610059;2．中石油川庆钻探工程有限公司 地球物理勘探公司，四川成都610213;3．成都理工大学 地球探测与信息技术教育部重点实验室，四川成都610059)

Kirchhoff叠前时间偏移关键参数分析与研究

顾 雯1，王铎翰2，阎建国3

(1．成都理工大学 信息工程学院，四川成都610059;2．中石油川庆钻探工程有限公司 地球物理勘探公司，四川成都610213;3．成都理工大学 地球探测与信息技术教育部重点实验室，四川成都610059)

叠前时间偏移已经成为地震资料处理的常规手段之一，在构造复杂但速度横向变化不大时，应用克希霍夫叠前时间偏移方法，一般可以得到较好的成像效果。但是叠前时间偏移是一项系统工程，一些配套技术的选取和一些关键参数的选取，直接影响到成像结果。这里根据OMEGA2处理系统制定的叠前时间偏移的处理方法和流程，对叠前时间偏移处理的配套技术和关键参数(叠前道集偏移距分组、偏移孔径和倾角选取、均方根速度建模、旅行时算法)进行了分析总结，结合试验程序进行了研究和讨论，并提出了关键参数选取的基本原则，对实际处理工作具有一定的应用价值。

克希霍夫叠前时间偏移;偏移成像;关键参数

0 前言

随着勘探与开发要求的不断提高，地震勘探越来越关注复杂构造的精确成像。影响复杂介质成像的主要原因在于:地层倾角大，横向速度变化剧烈，断层发育，埋藏较深等方面。地震偏移技术正是为了满足这一需求而不断发展和完善起来的。地下介质的偏移归位处理，既可以在叠加之前进行，也可在叠加之后进行。前者叫叠前偏移，后者叫叠后偏移。按其实施的领域，还可分为时间偏移和深度偏移。

在四川地区，工区地貌为典型的丘陵和高山地貌。由于地面海拔相对高差大，地势险恶，沟壑纵横，地形切割厉害，纵向、横向速度变化大，所以使用叠后偏移难以得到理想的成像效果，影响地质任务的完成。作者在本文中，结合四川工区实际地震资料，主要围绕影响Kirchhoff叠前时间偏移效果的关键参数进行分析探讨，总结了影响其成像效果的原因，实现了试射法旅行时计算程序，研究了不同旅行时计算方法的应用效果，最后提出了关键参数选取的基本原则，这对于实际资料处理具有一定的参考价值。

1 Kirchhoff叠前时间偏移原理和方法

1．1 偏移的概念

地震波偏移成像即通过波场外推，将炮检点逐渐向绕射点延拓。其中，绕射曲线会逐渐收敛，最终波场外推到绕射点的深度，绕射曲线收敛到绕射点上，其本质就是把数据域中的绕射波，收敛到模型空间中，并产生绕射的空间点。简而言之，地震偏移成像就是一个收敛绕射波的过程［2]。

1．2 Kirchhoff绕射积分中三个因子的含义

作者基于二维处理的Kirchhoff的积分，在二维情况下，可将积分公式简化为式(1)［1]。

式(1)中结合了倾斜因子cosφ，该因子表示为传播方向与垂直轴z之间夹角的余弦［4];球面扩散因子在二维波动空间中用表示［4];子波整形因子利用计算波场的半导数，如式(1)中项，这同45°相移和振幅谱用频率的校正是等价的(此时的速度V为均方根速度)［4]。

(1)倾斜因子。点孔(反射或绕射)得到的波前振幅与角度有关，所以在求和前要考虑到倾斜因素构成的振幅依赖角度的关系。

(3)子波整形因子是关于惠更斯二次震源波形的相干性。惠更斯二次震源作为子波响应，它在双曲线轨迹各点必然具有一定的相位和频率特性，否则，当它们互相靠近时，就不会有振幅相消的现象。对2D偏移，设计一个45°常相位谱，振幅谱正比于频率平方根;对3D偏移，这个因子的相移为90°，振幅谱与频率成正比［4]。

1．3 Kirchhoff绕射偏移中的孔径概念

Kirchhoff偏移是沿着绕射双曲线作振幅叠加。在理论上，一条绕射双曲线在时间和距离上可以无限延伸，而实际中，我们只能截取有限段作为求和路径，截取空间范围，即实际求和路径宽度，称为偏移孔径［4]，如图1所示。

图1 虚线范围内为计算的偏移孔径Fig．1 The diagram showing the migration aperture selection:dotted lines for the calculation of the offset within the aperture

绕射双曲线的曲率由速度函数决定。低速双曲线的孔径与高速双曲线的孔径相比窄一些，这一点符合我们的直觉。即速度高意味着偏移量大，而一般高速度层伴随着的是地层深度向下纵伸。

2 Kirchhoff偏移处理

2．1 资料处理流程

此次地震数据来自四川某工区2008年AAA三维地震资料，我们选取第20线(主测线)为例，结合工区地貌为典型的丘陵和高山地貌，地面海拔相对高差大，沟壑纵横，地形切割厉害，纵向、横向速度变化大的特点，采用叠前偏移处理，取得了较好的成像。

从图2可以看出，在叠前时间偏移处理时，速度模型需要反复修改，它是影响资料处理进度的关键。

图2 叠前时间偏移流程图Fig．2 Flow chart of pre－stack timemigration

将08AAA20地震测线数据进行预处理，可以得到水平叠加剖面(见图3)。由图3中可见，剖面的横向分辨率十分模糊。

图3 08AAA20线的水平叠加剖面Fig．3 Stack profile of08AAA20 line

在CMP点从1 700和2 100附近可以看见层位有明显的交叉，这是背斜构造的明显标志。

图3的叠加剖面中背斜构造变宽，但同向轴在结合部发生了交叉，不能准确反映地下构造情况。

2．2 Kirchhoff偏移处理成像结果

在Kirchhoff偏移模块选取偏移距分组、偏移孔径和倾角选取、旅行时算法的参数进行计算，可得到如图4所示的偏移结果。

图4 08AAA20线偏移后成图Fig．4 Migration profile of 08AAA20 line

与图5(a)的水平叠加剖面对比可明显看出，在给定参数下的Kirchhoff叠前时间偏移的效果。散射点、回转波得到收敛，地层背斜明显，偏移后横向成像效果得到明显提高。

3 Kirchhoff偏移参数分析

3．1 偏移距分组

偏移距分组即是实现等效偏移距偏移(EOM)成像。将克希霍夫时间偏移的双平方根方程(DSR)，转化为一个单平方根方程，使输入采样在没有发生时移的情况下，映射到以等效偏移距为变量的共散射点道集(CSP)上，使散射能量按照双曲线规律分布，之后在CSP道集上应用Kirchhoff动校正并叠加。

分好组后，不同的偏移距分组通过公式(单平方根方程)，可以计算出各自所对应的共散射点道集(CSP)，对各自同一CMP道集内具有相同偏移距的道进行叠加。

通过分贝谱(见下页图6)和对数能量谱(见下页图7)可以看出，不同分组下各自剖面的差异。其中，采用五组的分组方式，在分贝谱和对数能量谱的高频部份，会出现明显的噪音干扰。

3．2 偏移孔径和倾角

偏移孔径和倾角选取是影响Kirchhoff偏移的重要参数。偏移孔径的宽度是用所占的地震道数来度量的［4]。倾角是在确定合理孔径后，对其相应时间上的偏移孔径，利用倾角进一步控制孔径，其目的是提高偏移质量和节约运行时间。

在08AAA20研究工区上，结合偏移孔径和倾角参数的范围变化，分别选取了范围在1 000 m、2 500 m、4 500 m、6 000 m下的偏移剖面(见下页图8)。

偏移孔径和倾角参数的范围变化在1 000 m时，偏移剖面的横向分辨率十分低，背斜边界陡倾角不能正确成像，绕射没有很好的归位，剖面面貌差;在2 000 m时背斜成像变得清晰，但是深部的噪音影响依旧严重;随着范围的不断增大，在4 500 m和6 000 m时，剖面整体成像效果很好。

图5 偏移前后构造部位对比Fig．5 Comparison of the construction site before and aftermigration

图6 5组、100组、30组的分贝谱Fig．6 dB spectrum of 5 groups，100 groups and 30 groups

图7 100组、30组、5组的对数能量谱Fig．7 The logarithmic energy spectrum of 100 groups，30 groups and 5 groups

图8 不同偏移孔径下的偏移成像Fig．8 Themigrated images under differentmigration aperturs

3．3 偏移速度的选取

速度是偏移计算中的又一重要参数，之前进行的偏移计算，都是基于偏移距分组之前的速度分析所提供的速度进行计算。在利用Kirchhoff叠前时间偏移得到时间域CRP道集后，通过反动校正交互拾取速度谱，可建立均方根速度模型。只有在满足该点的均方根速度时，才会出现拉平。否则，只会出现上翘(速度过小)或下弯(速度过大)［8]。

图9是将拾取的速度进行0.8倍、1.2倍的速度变化，对剖面进行偏移成像。可以看到，随着速度的增加，背斜构造顶端的同向轴由0.8倍图像中的下弯，到1.2倍图像中同向轴上翘。

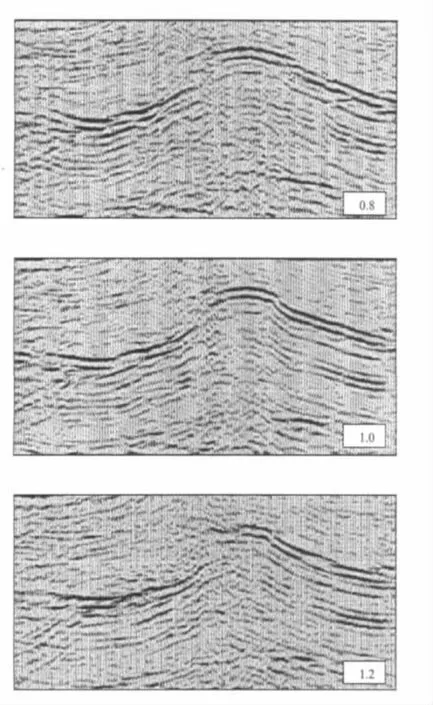
图9 不同速度场下的剖面面貌Fig．9 The profiles with different velocity fields

在实际运算中，由于选取的是弯曲射线旅行时，采用的是层状速度模型，上面均方根速度的提取，是为了提取层速度参与运算(是在整体速度选好后，对每个速度解释点进行的0.8倍、1.2倍的速度扫描)。

3．4 旅行时的算法

在时间偏移假设在水平层状介质的基础上，Kirchhoff叠前时间偏移利用均方根速度模型计算旅行时。而在实际工区的研究中，由于选取的Kirchhoff弯曲射线叠前时间偏移，采用的是层状速度模型。上面提到的均方根速度的提取，通过变换求出层速度来参与运算。

在生产中，主要采用直射线法进行旅行时间的计算。式(2)是弯曲射线偏移的旅行时间公式［6]。

直射线法采用了式(2)的前二项进行计算，在高阶的计算精度上不如弯曲射线法。

图10 水平层状介质下两种算法的计算路径Fig．10 The path of two algorithms for horizontal layered media

试射法通过循环迭代的方式，统计每一层的旅行时，较之直射线法和弯曲射线法在旅行时的计算上更为准确。我们编制了试射法的C语言程序，并将它用到了叠前时间偏移的旅行时计算中，取得了一定效果。下面将讨论三种算法在水平层状模型中的旅行时间差。

假设一个四层模型，速度是V1=2 000 m/s、V2=3 000 m/s、V3=4 000 m/s，到每层底部界面的双程旅行时是1 s、2 s、3 s、4 s，代入偏移距范围是500 m～12 000 m。

采用试射法计算、弯曲射线法进行旅行时间计算，通过模型正演的结果见表1

通过表1和图11可以看出，随着偏移距的增大，弯曲射线旅行时计算的旅行时，与试射法的旅行时差值越来越大。

在模型的对比中也发现，当选取偏移距与埋深相差不大时，其计算的结果也是相差无几的。只有在偏移距远大于目的层埋深时，采用试射法较之另外两种方法更为准确。

对比图13和图14的剖面，两种方法在大偏移距下，对剖面构造主体(构造相对复杂)的成像效果影响更为明显。

表1 不同旅行时间算法的计算结果Tab．1 Computation results of different travel time computingmethods

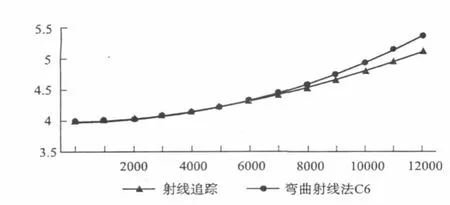
图11 对比试射法和弯曲射线在不同偏移距下的旅行时间差Fig．11 Comparison of testmethod and bending rays travel under different offset time difference

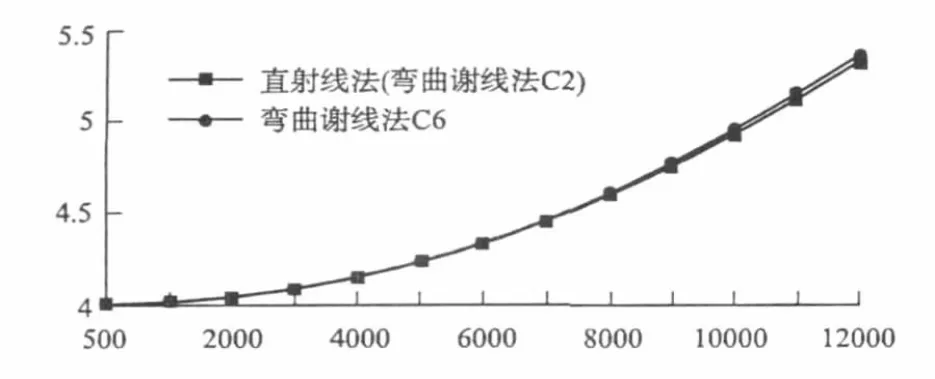
图12 对比直射线法和弯曲射线在不同偏移距下的旅行时间差Fig．12 Comparison of direct linemethod and bending rays travel under different offset time difference

在表2中我们可以看见，弯曲射线法比直射线法采用更高阶的运算，在偏移距较小时，直射线法与弯曲射线法计算的旅行时间差可以是忽略不计的;而在偏移距变大时，弯曲射线法的高阶项对曲线精度的计算也没有太大的实际价值。因此，在实际中人们采用弯曲射线法时不愿意采用高阶项，而通常把偏移距x控制在很小的数值，以消除计算上的影响(与偏移距分组相联系)。

图13 试射法在偏移距7 000 m的剖面Fig．13 The section of testmethod in the 7000m cross－section offset

图14 弯曲射线法在偏移距7 000 m的剖面Fig．14 The section of bending raymethod in the 7000mcross－section offset

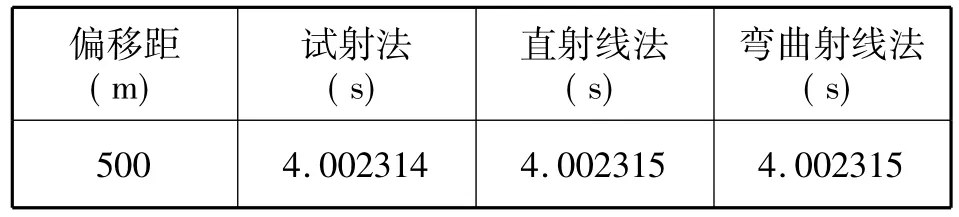
表2 小偏移距各种旅行算法的时间差Tab．2 Time difference of travel time algorithm in a variety small－offset

在实际运用中，应结合工区实际要求情况来选取适合的旅行时间算法。

3．5 关键参数的选取原则

(1)偏移距分组原则:在实际的生产过程中，同一偏移距组的空道，应控制在30%以内。对所缺的偏移距补充零道，使每一个CMP道集内偏移距分布尽量均匀、齐全。此外，若选用覆盖次数低的小偏移距道集，偏移处理后就会填充上假的大偏移距数据，这样的道集求取的速度会影响之后速度拾取时的精确度［10]。

(2)偏移孔径选取原则:当偏移孔径取值小时，由于不能含盖成像带范围，将损失掉陡倾角信息，偏移剖面会出现畸变现象。偏移孔径越大，由于含有大量来自其它反射点的波场，偏移剖面噪音会加重，降低了剖面信噪比，还增加了机器的运算时间，因此可以先根据目的层的深度选取偏移孔径大小。在首次选取偏移孔径大小时，应与目的层深度相同，保证目的层位信息量的获取，再进行实验验证，选取合适的偏移孔径大小。

(3)速度的选取原则:经预处理后，叠加剖面速度的选取，基本符合地下地质情况，偏移归位使速度谱能量更加收敛。从能量谱入手，不断细化速度的选取，建立更加准确的速度模型。

(4)旅行时间计算方法的选取原则:试射法作为一种高级旅行时间算法，在精度上比其它二种算法更符合地下实际地层速度分层。在地下地质结构相对简单，偏移距不大的情况下，算法对于剖面成像影响不大。但在地下地质结构复杂，采用大偏移距接收地层信息时，采用试射法更符合地下地层的信息的求取。

4 结束语

通过参与四川工区08AAA20线地震资料叠前时间偏移处理工作，得出以下几点体会和认识:

(1)叠前时间偏移并不是一个独立的处理过程，其成像效果与基础处理密不可分。叠前时间偏移要求输入经过基础处理的高质量道集数据，数据具有较高的信噪比，振幅能量均匀，且不存在静校正影响。因此在基础处理中，应着重做好振幅恢复与补偿、叠前去噪、子波处理、速度分析与静校正迭代等工作，为叠前时间偏移打下良好的基础［3]。

(2)速度场是直接影响偏移结果的关键，合理的、接近地质真实的、高精度的速度模型，是叠前时间偏移获得高质量效果的前提。叠前时间偏移除了其算法本身外，剩下的工作主要就是建立速度模型，而建立速度模型是一个复杂而费时的迭代过程［9]。

(3)对偏移孔径的实验，可以在偏移质量和偏移效率中寻找到最佳的结合点。

(4)在信噪比问题上，Kirchhoff积分法有其固有理论上的缺陷:即原始地震道上的任何一个样点幅值，不管它是信号还是噪声，都参与运算。有效波信号符合反射波传播路径规律，会被正确地偏移归位;而某些幅值较大的噪声经偏移算子改造后，放到偏移孔径范围内的所有网格点上，无法相互抵消，形成画弧现象，降低了叠前时间偏移的成像质量［7]。

［1]贺振华．反射地震资料偏移处理与反演方法［M]．重庆:重庆大学出版社，1989．

［2]路基孟．地震勘探原理下册［M]．北京:中国石油大学出版，2006．

［3]张颖．三维地震叠前时间偏移处理技术应用与展望［J]．石油地球物理勘探，2006，36(05):174．

［4]渥·伊尔马兹．地震资料分析［M]．刘怀山，王克斌，童思友，等译．北京:石油工业出版社，2006．

［5]EKOROMARIUSBLANCHARD，GU HANMING．Prestack Kirchhoff Time Migration for Imaging of Complex Structure in the Nanyang Oilfield［J]．The leading edge，2007，4(2):101．

［6]P．赫布拉尔Th．克雷．根据地震反射波旅行时测定——计算层速度［M]．北京:石油工业出版社，1987年．

［7]WANG DI，WANG HUAZHONGl，MA ZAITIANL，et al．Review of prestack time migration methods［J]．Geophysics，1984，49(11):2064．

［8]徐基祥，崔化娟．叠前时间偏移解析速度分析［J]．石油地球物理勘探，2004，39(2):126．

［9]李建明，杨品荣．地震资料叠前时间偏移处理技巧与效果——以坦南断裂带为例［J]．石油地球物理进展，2002，07(02):38.

［10]麻三怀，杨长春，孙福利，等．克希霍夫叠前时间偏移技术在复杂构造带地震资料处理中的应用［J]．石油物探，2008，54(07):447.

P 631.4

A

1001—1749(2011)02—0140—07

2010－09－01改回日期:2010－12－29

顾雯(1986－)，女，四川成都人，硕士，现主要从事构造解释储层预测研究工作，同时也研究叠前时间偏移处理。