SPSW对钢框架结构体系抗震性能影响分析

史三元，穆金花

(河北工程大学土木工程学院，河北邯郸056038)

钢板剪力墙(steel plate shear wall，SPSW)的框架结构是一种适合于高烈度区的双重抗侧力体系，具有自重轻，抗震性能强，用钢量少等优点［1]。目前国内苏幼坡［2]、王迎春［3]等曾从 SPSW 在框架中的应用着手，对在框架中使用的SPSW进行了试验，提出了SPSW抗剪承载力的简化设计公式，证明SPSW可用于地震地区既有建筑的加固或者作为新建筑的抗侧力体系。截至目前我国对于SPSW的研究只局限理论方面，对于常用的钢板厚度变化范围和SPSW对周边框架柱刚度的影响等研究不足，使得现阶段SPSW在框架中的应用还不是很广泛［4]。本文从研究SPSW对钢框架的抗震性能影响出发，分别建立钢框架与SPSW厚度不同的钢框架—钢板剪力墙有限元分析模型，分析两种结构体系抗震性能的变化规律，探讨SPSW对钢框架结构体系抗震性能的影响，并进一步比较SPSW厚度不同对钢框架—钢板剪力墙结构体系抗震性能的影响。

1 有限元计算模型

建立了典型的3跨6层钢框架和钢框架－钢板剪力墙平面模型(图1)，截面设计符合在多遇地震作用下我国规范要求［5]。恒荷载gk=16 kN/m，活荷载qk=7 kN/m，抗震设防烈度为8度，Ⅱ类场地，第一组。梁柱截面尺寸见表1。

采用有限元软件SAP2000进行计算。材料采用Q235钢材，弹性模量 E=2.01×105MPa，泊松比μ=0.3，假定钢材均为理想弹塑性材料。

表1 框架杆件截面尺寸Tab.1 The components of the frame system

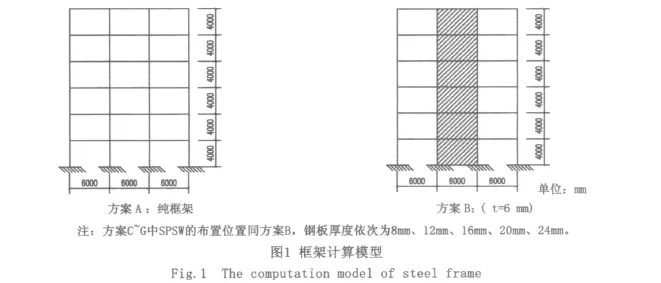
2 抗侧力分析

带SPSW的钢框架作为双重抗侧力体系，其整体刚度必大于普通钢框架［6～7]。本文先对结构顶点施加大小为10 kN的水平方向荷载进行简单分析，并计算结构的抗侧刚度进行比较。

柱抗侧刚度D是指柱节点有转角时使柱端产生单位位移所需施加的水平推力。钢框架D计算公式如下［8]:

其中，α—刚度修正系数;ic—柱线刚度，ic=EIc/h，EIc为柱抗弯刚度;h—层高。钢框架—钢板剪力墙D计算公式为［8]

其中，V—结构剪力;δ—结构平移变形的层间位移。

计算结果如表2所示。可以看出，带SPSW的钢框架结构的抗侧刚度远远大于钢框架结构，SPSW厚度为6 mm的钢框架－钢板剪力墙的抗侧刚度为是普通钢框架结构的9.681倍，且随着SPSW厚度的增大钢框架－钢板剪力墙结构的抗侧刚度逐渐增大。

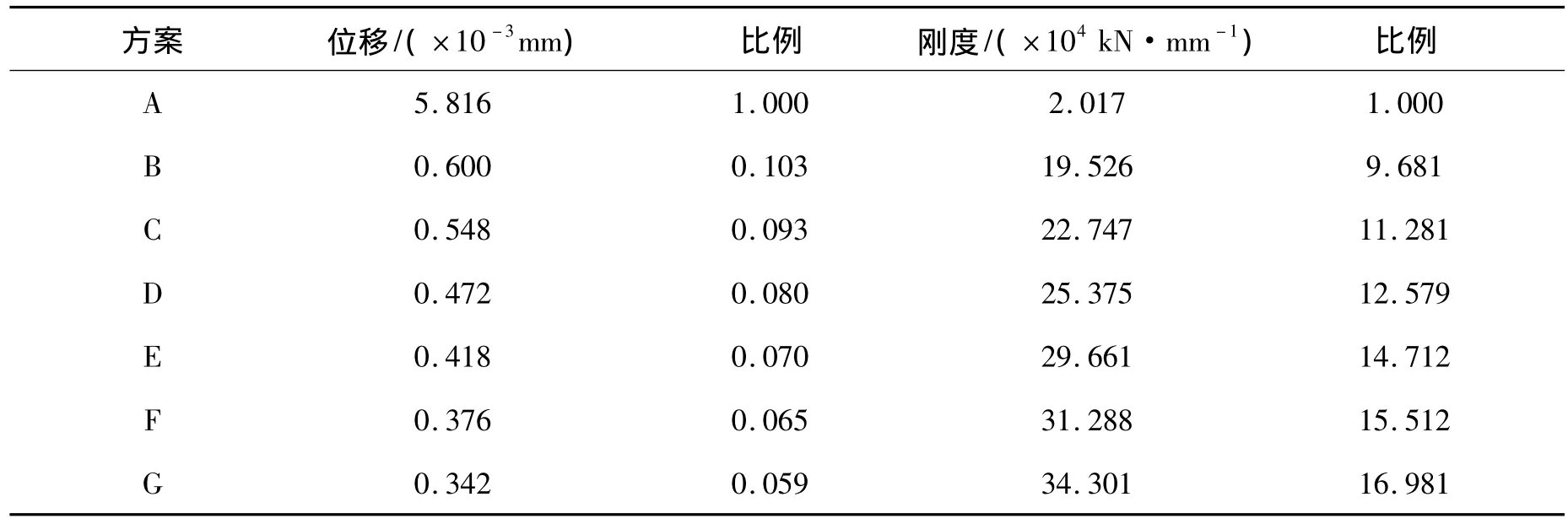
表2 结构的抗侧刚度Tab.2 The stiffness of the structure

3 模态分析

结构的模态(振型)分析用于确定结构的振型及其对应的自振周期，结构振型和自振周期是结构的固有特性，是反映结构动力特性的主要量，是结构动力分析的基础［9]。本结构模态的求解采用Ritz向量分析方法。Ritz向量法考虑了动力荷载的空间分布，可以为后面时程分析提供更精确的振型基础。

利用SAP2000计算不同方案的自振周期(表3)，可以得出该例中钢框架结构第一周期为1.6 s，反映了结构的整体刚度小的特点，而带SPSW的钢框架结构的自振周期要明显小于钢框架结构，并且各方案自振周期大小关系是:方案A＞方案B＞方案C＞方案D方案E＞方案F＞方案G。

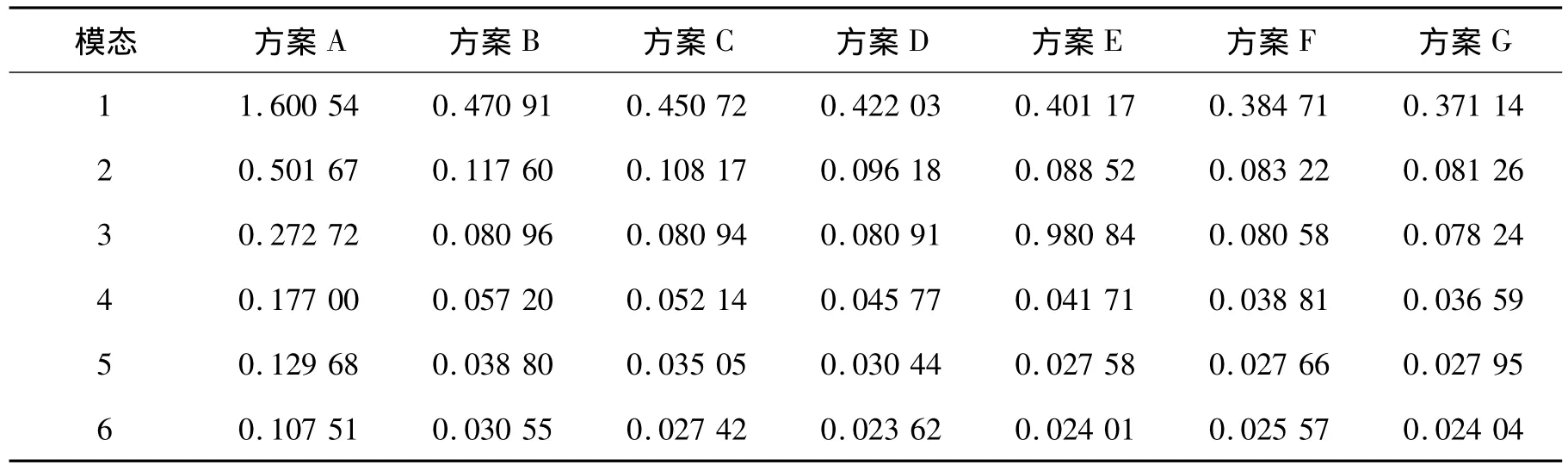
表3 结构的自振周期Tab.3 The natural vibration period of the structure s

4 时程分析

结构的地震反应的时程分析方法，是将地震波将地震输入，然后通过运动方程的积分求出地震持续时间内结构的内力和变形随时间变化的过程，是一种直接动力法，能比较真实的描述结构地震反应的全过程。时程分析方法建立在动力方程的基础上，动力平衡方程形式如下［10]:

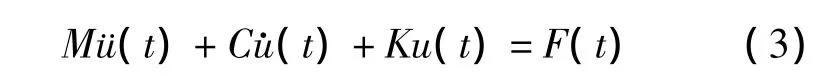
其中t—时间;K—刚度矩阵;C—阻尼矩阵;M—对角质量矩阵;u—结构的位移。

本文采用比较典型的El－Centro加速度时程波对结构进行计算分析。罕遇地震取400 cm/s2，时间间隔均为0.02 s，共作用30 s。

鉴于SPSW框架结构的时程曲线较为接近，以方案A、方案D为例，比较了2种框架结构在El－Centro波400 cm/s2加速度作用下，顶点位移及基底剪力时程曲线(图2)。可以看出，带SPSW的钢框架结构的顶点位移明显小于钢框架的顶点位移，钢框架结构所受基底剪力明显小于钢框架—钢板剪力墙结构体系。

表4列出钢框架及SPSW厚度不同的的钢框架－钢板剪力墙在El－Centro波400cm/s2加速度作用下的顶点最大位移，可以看出钢框架结构顶点位移最大值为43.96mm，SPSW厚度为6 mm的钢框架－钢板剪力墙顶点位移最大为16.70mm，24 mm的钢框架－钢板剪力墙顶点位移最小为10.41mm，即随着SPSW厚度的增加，钢框架－钢板剪力墙位移逐渐减小。

表4 顶点最大位移值Tab.4 The maximum of vertex displacement

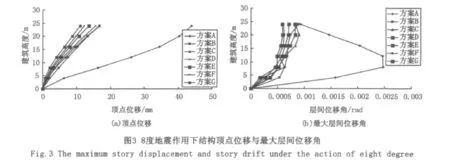
由结构的顶点位移和层间位移角之间的关系如图3所示，可以看出钢框架结构的最大层间位移角出现在第二层，内填钢板后结构的最大层间位移角上移而且没有明显的薄弱层;当SPSW≥20 mm时，由于结构的刚度很大，顶点位移很小，但在下部产生较大的层间位移;SPSW≤6 mm时，结构底部位移明显增大;SPSW厚度在8～16 mm范围内结构呈现较好的层间位移协调工作变形曲线，效果最佳。

5 结论

1)SPSW可以显著提高钢框架结构的抗侧刚度，减小层间位移，即对控制结构在水平力作用下的侧向变形非常明显，适合应用于8度地区，而纯钢框架结构体系则会出现明显的薄弱层，不适宜8度地区使用。

2)SPSW厚度不同的钢框架－钢板剪力墙结构在El－Centro波400 cm/s2加速度作用下，顶点位移变化趋势基本一致。随着SPSW厚度的减少，结构顶点位移逐渐增加。

3)在实际应用中应充分考虑钢框架与SPSW的协调变形能力，充分发挥SPSW的作用，选择合适的钢板厚度。该文中所举结构体系在SPSW厚度为8～16 mm时，表现效果最佳。

［1] 郭彦林，董全利.钢板剪力墙的发展与研究现状［J] .钢结构，2005，20(1):1－6.

［2] 苏幼坡，刘英利，王邵杰.薄钢板剪力墙抗震性能试验研究［J] .地震工程与工程振动，2002，22(4):81－84.

［3] 王迎春，郝际平，李峰，等.钢板剪力墙力学性能研究［J] .西安建筑科技大学学报:自然科学版，2007，39(2):181－185.

［4] 朱华.多高层钢结构住宅结构体系及钢板剪力墙体系综述［J] .中国建材科技，2009(6):56－60.

［5] GB50011－2010，建筑抗震设计规范［S] .

［6] 史三元，郭维光，陈鑫，等.高层钢结构抗震体系的力学性能分析［J] .河北工程大学学报:自然科学版，2008，25(4):1－3.

［7] 史三元，侯桂欣，苏晓亮，等.小高层钢结构住宅抗震性能研究［J] .河北工程大学学报:自然科学版，2010，27(2):12－15.

［8] 方鄂华，钱稼茹.高层建筑结构设计［M] .北京:中国建筑工业出版社，2008.

［9] 陈昌宏.SAP2000结构工程案例分析［M] .北京:冶金工业出版社，2010.

［10] 王社良.抗震结构设计［M] .武汉:武汉理工大学出版社，2010.