引入方向变量的群机器人启发式区域覆盖算法

李慧勇，张国有，郭银章

（1.太原科技大学计算机学院，太原 030024；2.山西工程职业技术学院计算机工程系，太原 030009）

机器人全区域覆盖问题是指携带有一定探测范围的传感器（如激光、声纳等）的机器人覆盖整个环境并创建环境地图的过程。该问题的本质是机器人或机器人团队利用其移动性将其感知范围逐步覆盖整个环境。群机器人学［1］是机器人学与群体智能交叉形成的一个新的学科和研究方向，利用群体机器人进行区域覆盖与传统的单机器人区域覆盖相比，可以加快覆盖速度，提高覆盖效率，节约成本，在军事、科研以及生产生活中有广泛的应用，例如:未知区域的地形测绘、未知水域的排雷、抢险救灾中的废墟探测、汽车轮船的检修或喷漆、室内外清洁等。

研究群机器人全区域覆盖问题，首先要建立环境地图的模型。目前环境地图的建模方法有:栅格法［2］、单元分解法［3］、拓扑逻辑图法［4］和 voronoi图法［5］等。在环境地图的模型建立后，群机器人的覆盖路径规划算法是区域覆盖问题的核心。目前已有的算法可以分为两类:离线规划算法和在线规划算法。Diana和Wesley等［6］用拟态物理的方法实现了群机器人的全区域覆盖，机器人之间采用显式通信方式。这种群机器人区域覆盖算法的一个局限是机器人群体在区域覆盖过程中，机器人之间的距离有一定限制。I.Wagner［7］和 S.Koenig 等［8］受蚂蚁等群体性昆虫运动时在路上留下信息素的启发，提出了群机器人启发式全区域覆盖算法:群体机器人通过在覆盖区域留下的信息素进行隐式通信从而完成对目标区域的覆盖。这类算法对群机器人中机器人之间的距离没有限制。在基于T.Balch等［9］提出的NC（Node Counting）算法的群机器人启发式全区域覆盖算法中，机器人每次完成更新当前栅格的值和移动到下一个栅格两个动作。其中，机器人每次移动到一个栅格后，给这个栅格的值加1，然后移动到与其相邻且值最小的那个栅格中，最后完成全区域覆盖。后来，I.Wagner等［7］改进了其中的更新栅格值策略，提出了WVU（Wagner's Value-Update Rule）算法，该算法较原算法全区域覆盖时间明显降低。S.Koenig等［8］将人工智能领域的LRTA（Learning Real-Time A）算法借鉴到更新栅格值的策略中，还有 S.Thrun［9］提出的 TVU（Thrun's Value-Update Rule）算法，都在一定程度上减少了机器人的区域覆盖时间。

由于群机器人启发式全区域覆盖算法的并行性，会产生多个机器人相遇，并且同时占据某个栅格的情况，因此增加了完成区域覆盖的时间。如果能够减少机器人的相遇次数，可以在一定程度上减少机器人群体的重复移动次数，从而提高算法的覆盖效率。

通过对NC、WVU、LRTA、TVU四种群机器人启发式全区域覆盖算法的分析，在原有算法基础上引入了方向变量。引入方向变量的新算法中，方向变量存放上一步机器人移动的方向，机器人每次移动尽量按照原来的方向前进，减少转向次数，从而减少了机器人相遇的几率，因此在一定程度上减少了机器人重复移动次数。同时由于减少了机器人转向次数，从而在一定程度上减少了机器人在实际应用中因为转向而造成的能量损耗。

图1 机器人和栅格地图Fig.1 Robot and grid map

1 群机器人启发式全区域覆盖算法

在栅格地图环境中，群体机器人中的个体机器人只有局部感知能力，个体机器人的感知范围如图1（a）中白色区域所示。设未被覆盖的栅格值为0，覆盖过的区域栅格值为一个正整数，如图1（b）所示；机器人每次只能判断与其相邻的A、B、C、D四个方向栅格的值；群体机器人中每个机器人的移动能力有限，每次只能移动至与其相邻的 A、B、C、D四个栅格之一；机器人可以同时占据一个栅格；群机器人在开始区域覆盖前的位置随机分布在栅格地图中。

最基本的NC算法［10］（Node Counting）如下:

Step 1 求出A、B、C、D四个栅格中值中的最小值；

Step 2 机器人将当前占据的栅格值加1；

Step 3 机器人移动到值最小的栅格中，如果有若干栅格值都等于最小值则随机移动到其中一个栅格中，转到Step 1.

该算法简单明了。由于机器人每次到过一个栅格后就把该栅格的值加1，因此栅格的值越小，说明栅格被访问的次数越少。机器人每次都向没有被访问过或者比较少访问过的栅格移动，因此最后可以完成整个栅格地图的覆盖。后来提出来的改进算法主要是针对NC算法的Step 2进行修改。设当前栅格值为u，下一步要移动到的那个栅格值为u_next，则NC算法的Step 2可以用等式u=u+1表示。WVU算法［7］中更新策略是:if（u＜=u_next）then u=u+1.LRTA 算法［8］的更新策略是:u=u_next+1.TVU 算法［10］的更新策略是:u=max（u+1，u_next+1）.这些算法都是通过修改原有NC算法中的栅格值的更新策略，在一定程度上减少了机器人完成区域覆盖所需时间。

但是，在上述四种算法的改进中，没有考虑到多个机器人相遇，同时占据某个栅格，从而产生对栅格的重复覆盖的问题。如何能够尽量减少机器人的相遇次数呢?下面比较一下同一栅格地图环境下，相同数量机器人执行同一覆盖算法，从相同位置出发，走不同路径，移动相同次数后，所形成的不同覆盖区域。

图2为执行WVU算法的两个机器人在10×10栅格地图环境下，移动8次后，走不同路径，可能形成的若干种覆盖区域中的三种不同覆盖区域。在图2中，值为0的栅格表示没有被覆盖，值为1表示栅格已经被覆盖过一次，值为2表示栅格被覆盖过2次。为区别不同的两个机器人的覆盖路径，分别用横线栅格和斜线栅格来区分不同机器人覆盖过的栅格。用（x，y）来表示机器人在栅格地图中所处的位置（其中x表示行坐标，y表示列坐标）。图2中两个机器人的出发点分别是（2，4）和（2，6），其中图2（a）中机器人移动路径分别是:（2，4）→（3，4）→（4，4）→（5，4）→（6，4）→（7，4）→（8，4）→（9，4）和（2，6）→（3，6）→（4，6）→（5，6）→（6，6）→（7，6）→（8，6）→（9，6）；图 2（b）中的机器人移动路径分别是:（2，4）→（3，4）→（4，4）→（5，4）→（5，5）→（5，6）→（5，7）→（5，8）和（2，6）→（3，6）→（4，6）→（5，6）→（6，6）→（7，6）→（8，6）→（9，6）；图 2（c）中机器人移动路径分别是:（2，4）→（3，4）→（3，5）→（4，5）→（4，6）→（5，6）→（5，7）→（6，7）和（2，6）→（2，6）→（3，5）→（3，6）→（4，6）→（4，7）→（5，7）→（5，8）。图2（a）中，机器人没有重复覆盖区域，共完成覆盖16个栅格；图2（b）中，有一个重复覆盖栅格，栅格（5，6）被两个机器人重复访问，共完成覆盖15个栅格；图2（c）中，有三个重复覆盖栅格，机器人共完成覆盖13个栅格。可见，相同的机器人数量，同样的移动次数，同样的算法下，不同的覆盖路径，图2（a）覆盖区域最大，图2（c）覆盖区域最小。从图2的比较中可以看出，机器人的移动路径转向次数越少，相遇几率就越小。相遇几率越小，那么相遇并同时覆盖一个栅格的情况就越少。因此，减少机器人在覆盖过程中的转向次数，可以在一定程度上减少栅格的重复访问次数，提高机器人的区域覆盖效率。

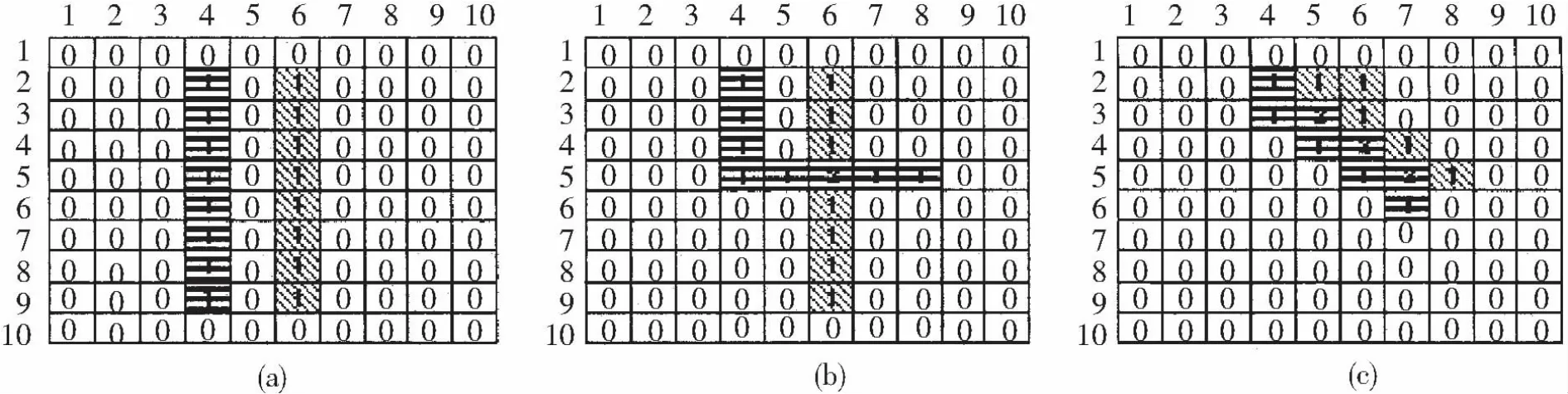
图2 两个机器人执行WVU算法的不同覆盖区域Fig.2 Different covering terrains of two robots executing WVU algorithm

另一方面，群机器人在进行区域覆盖的实际应用过程中，如果机器人个体在覆盖过程中能够尽量沿直线运动，则其能量消耗是较少的。如果机器人在行进中转向，则其要进行减速，转向，加速三个运动状态的转换，根据牛顿定律，转向过程中是要消耗一定的能量的，转向次数越多，这种额外能量损耗越大。设一次转向过程中机器人的能量损耗为e，则图2（a）中机器人能量损耗为0，图2（b）中机器人能量损耗为e，图2（c）中机器人能量损耗为12e.可见，机器人按照相同的区域覆盖算法，走不同的路径，移动相同的次数，会产生不同的额外能量损耗，而且差别较大。

群机器人执行相同的启发式全区域覆盖算法，之所以转向次数会产生如此大的差别，是因为在该类算法的Step 3中，当机器人相邻栅格中出现多个等于最小值的栅格时，机器人的移动方向是随机的。在这种情况下，如何能使机器人尽量按照原来的运动方向移动，从而尽量减少机器人的转向次数，是修改算法的切入点。

2 引入方向变量的群机器人启发式全区域覆盖算法

如图1（a）所示，设机器人每次移动的四个方向为A、B、C、D，引入机器人方向变量 m，m 的值可以取A、B、C、D之一。移动变量m中存放的是机器人前一次的移动方向，机器人每次移动完成后更新方向变量m的值。引入方向变量后的群机器人启发式全区域覆盖算法中，机器人首先求出其相邻四个栅格值中的最小值，然后和m方向栅格的值比较，如果相等，则机器人移动到m方向栅格中，并按照算法规则更新原占据栅格的值；如果不等，则机器人移动到栅格值最小的那个栅格中，如果有若干栅格值都等于最小值，再随机移动到其中之一。

根据上述思路，引入方向变量后的群机器人启发式全区域覆盖算法如下:

Step 1 求出A、B、C、D四个栅格值中的最小值；

Step 2 如果方向变量m方向的栅格值等于最小值，则机器人更新当前栅格的值，并移动到m方向的那个栅格中，然后转到Step 1；否则转到Step 3.

Step 3 机器人更新当前栅格的值并且移动到值最小的栅格中，如果有若干栅格值都等于最小值则随机移动到其中一个栅格中，并且更新方向变量m的值，然后转到Step 1.

引入方向变量后，原来群机器人启发式全区域覆盖算法中的NC算法、LRTA算法、WVU算法和TVU算法，分别形成了NC-M算法、LRTA-M算法、WVU-M算法和TVU-M算法。在图2的实例中，如果机器人执行引入方向变量的区域覆盖算法，只可能出现图2（a）中的移动路径，不会出现图2（b）和图2（c）那种移动路径，从而减少了机器人相遇并同时覆盖某个栅格的几率，在一定程度上减小了机器人的重复覆盖率，并且由于减少了机器人在行进过程中的转向次数，在一定程度上减少了机器人因为转向而造成的额外能量损耗。

3 仿真实验

通过仿真程序来验证改进算法的有效性。仿真程序由C语言编写，栅格地图在仿真程序中由一个二维数组表示，数组元素的值代表栅格的值。在栅格地图中每个栅格的初值为0，边界栅格的值为一个很大的数（使边界栅格在区域覆盖过程中不被访问）；机器人初始位置随机；机器人从一个栅格移动到相邻的栅格中为一次移动，机器人移动一次所花的时间为单位时间；机器人每次移动可以更新当前栅格的值；当所有栅格的值都为非0时，表示全区域覆盖结束；实验环境地图采用40×40栅格地图。

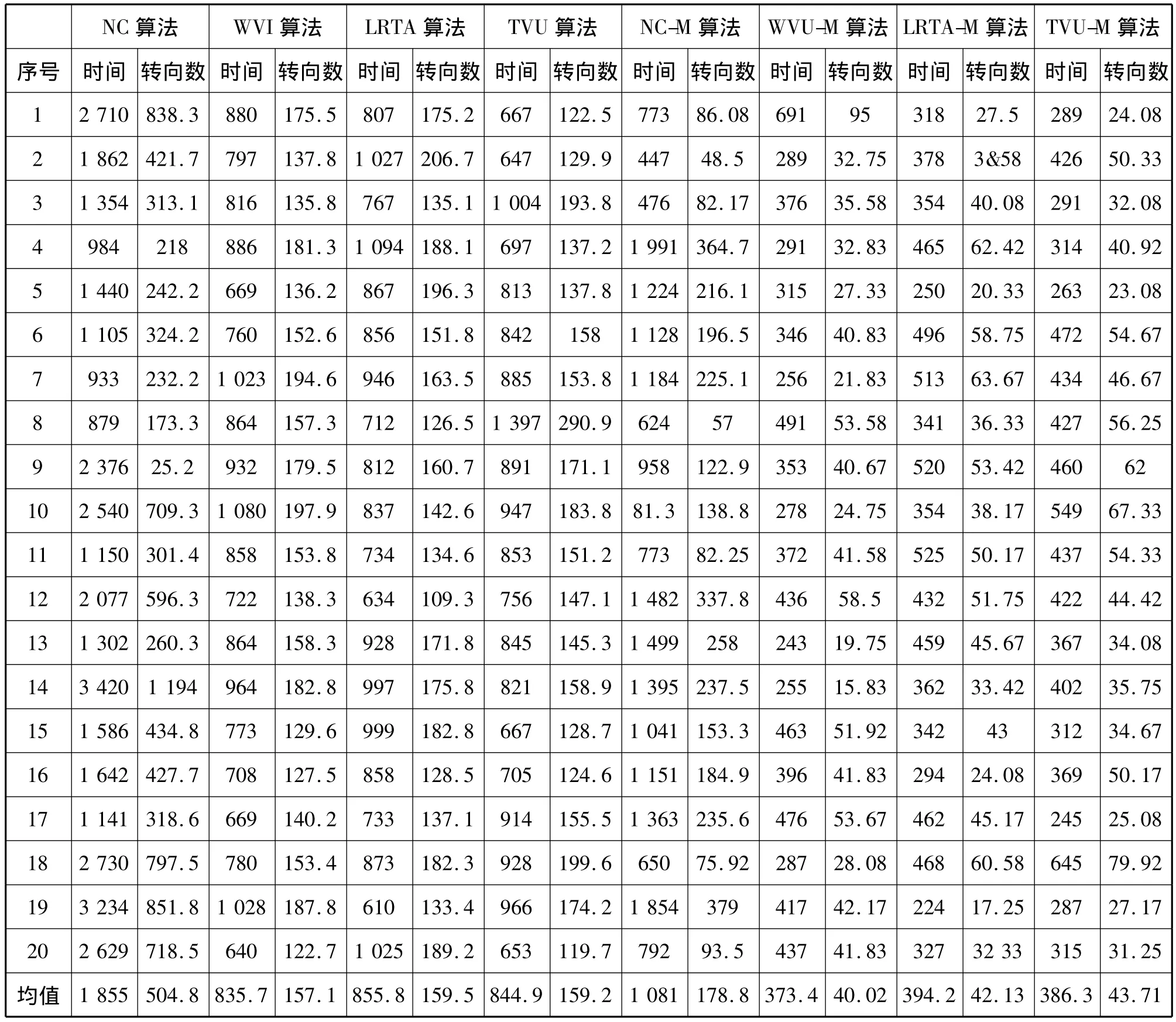
表1 12个机器人实验结果Tab.1 The experimental results of 12 robots

12个机器人分别采用8种不同的群机器人启发式全区域覆盖算法，对实验地图进行区域覆盖的结果如表1所示，其中的覆盖时间为群机器人完成一次全区域覆盖所花的时间，转向数为完成一次全区域覆盖每个机器人的平均转向次数。由于该类算法是随机算法，因此每种算法进行20次试验，并在最后求均值。从数据中可以看出，群机器人使用引入方向变量后的四种新算法，完成一次全区域覆盖的平均时间仅为相应原算法的45%左右，平均转向次数仅为相应原算法的25%左右，将上述算法的实验均值数据用条形图表示如图3所示。

从图3中可以清晰地看出，引入方向变量后的WVU-M、LRTA-M和TVU-M三种算法是所有算法中覆盖时间最小和转向次数最少的，并且这三种算法效率相当。NC-M算法比NC算法效率也大大提高，但较其他三种算法仍然有很大差距。通过实验比较机器人数量对算法效率的影响，得出的数据如图4所示。

图3 12个机器人均值数据Fig.3 The average data of 12 robots

图4 不同数量机器人的均值数据Fig.4 Average data of different numbers of robots

图4中，横坐标为机器人个数，图4（a）中的纵坐标为机器人完成一次全区域覆盖的平均时间，图4（b）中的纵坐标为完成一次全区域覆盖，每个机器人的平均转向次数。从图4（a）中可以看出，每种算法中，随着机器人数量的增加，群机器人完成一次全区域覆盖的时间逐渐减少，其中TVU-M、LRTA-M和WVU-M三种算法效率相当，且在所有算法中，这三种算法所用时间最少。在图4（b）中，NC、WVU、LRTA和TVU四种算法的每个机器人的平均转向次数随着机器人数量的逐渐增加，在上下波动，没有明显下降趋势；而NC-M、WVU-M、LRTA-M和TVUM四种算法，每个机器人的平均转向数随着机器人数量的增加而逐渐下降，其中TVU-M、LRTA-M和WVU-M三种算法转向次数最少而且效率相当。

4 结论

在原有的群机器人启发式全区域覆盖算法中，引入方向变量，在方向变量的作用下，机器人在区域覆盖过程中尽量不改变原来的运动方向，减少了机器人之间的相遇次数，从而减少了不同机器人同时访问相同栅格而导致的重复覆盖，提高了算法的效率。

仿真实验验证了群机器人在完成一次全区域覆盖任务时，使用引入方向变量后的改进算法比原算法的平均覆盖时间减少一半左右，而且随着机器人数量的不断增加，平均覆盖时间不断减少。在8种比较算法中，TVU-M、LRTA-M和WVU-M三种算法的全区域覆盖时间最少，并且三种算法效率相当。

同时实验结果也表明，完成一次全区域覆盖任务，如果使用原来的算法，随着机器人数量的增加，每个机器人的平均转向次数并没有明显的降低而是在上下波动。而如果使用引入方向变量的新算法，每个机器人的平均转向次数随着机器人数量的增加而线性下降，尤其是TVU-M、LRTA-M和WVUM三种算法转向次数最少而且效率相当。

［1］薛颂东，曾建潮.群机器人研究综述［J］.模式识别与人工智能，2008，21（2）:177-185.

［2］YAMAUCHI B.Decentralized coordination for multi-robot exploration［J］.Robotics and Autonomous Systems，1999，29（2）:111-118.

［3］CHOSET H.Coverage of Known Spaces:The Boustrophedon Cellular Decomposition［J］.Autonomous Robots，2000，9（3）:247-253.

［4］SYLVIA C WONG，BRUCE A MACDONALD.A topological coverage algorithm for mobile robots［C］//Proceedings of the 2003 IEEE/RSJ Intl Conference on Intelligent Robots and Systems，Las Vegas，Nevada.2003:1685-1690.

［5］CHOSET H，BURDICK J.Sensor based planning I，The generalized Voronoi graph［C］//IEEE International Conference on Robotics and Automation，1995:1649-1655.

［6］SPEARS D F，KERR W，SPEARS W F.Physics-Based Robots Swarms For Coverage Problems［J］.Int J on Intelligent Control and Systems，2006，11（3）:11-23.

［7］WAGNER I A，LINDENBAUM M.MAC vs PC:Determinism and randomness as complementary approaches to robotic exploration of continuous unknown domains［J］.Int J of Robotics Research，2000，19（1）:12-31.

［8］KOENING S，SZYMANKI B.Efficient and inefficient ant coverage methods［J］.Annals of Mathematics and Artificial Intelligence，2001，31:41-76.

［9］THRUN S.Efficient exploration in reinforcement learning［R］.Pittsburgh:Carnegie Mellon University，1992.

［10］BALCH T，ARKIN R.Avoiding the past:A simple，but effective strategy for reactive navigation［C］//International Conference on Robotics and Automation，1993:678-685.