Cr中SIA辐照损伤的改进分析型嵌入原子法的分析

王博,路彦冬

(1石河子大学生态物理重点实验室,石河子832003;2石河子大学后勤管理处,石河子832003)

Cr中SIA辐照损伤的改进分析型嵌入原子法的分析

王博1,路彦冬2

(1石河子大学生态物理重点实验室,石河子832003;2石河子大学后勤管理处,石河子832003)

将MAEAM和MD模拟方法相结合,从原子尺度上研究Cr中哑铃(dumbbell)间隙的稳定结构,获得了哑铃SIA 在(001)和(110)表面的能量E,并计算了Cr中(110)和(111)哑铃SIA的形成能。结果表明:SIA处于Cr(001)和(110)面时,(110)哑铃SIA结构最为稳定;形成能的结果与用第一原理和其他的理论或实验方法获得的结果基本一致。

铬;改进分析型嵌入原子法;MD;哑铃;哑铃间隙子

在核辐照环境下,金属材料中粒子之间发生碰撞[1],点缺陷将不断产生。大部分点缺陷在很短时间内通过间隙子和空位的结合而消失,从而使金属材料性能发生变化。粒子辐照导致金属材料中稳定性发生变化[2],因此,间隙和空位缺陷问题长期以来引起了人们的广泛关注。在实验研究方面,有粒子散射谱(ISS)[3]、Auger能谱(AES)[4]和原子探针(FIM-AP)[5]等实验都对金属材料缺陷作过研究;在理论研究方面,有第一原理(Ab initio calculation)[6]、模特卡罗模拟方法(Monte Carlo,MC)[7]、有效介质理论(effective-medium theory)[8]、密度泛函理论(density functional theory,DFT)[9]等。基于准原子和密度函数理论,Daw和Baskes建立了嵌入原子法(EAM)[10],这一半经验方法先后成功的用于金属的点缺陷、表面结构和重构、表面偏析等特性的研究。但是该理论没有考虑晶体中原子电子密度分布的方向性。为此,Zhang等人在 EAM模型和Johnson的AEAM模型[11]基础上,建立了改进分析型嵌入原子法(MAEAM)[12]。Ma Fe,Zhang Ji M等[13-16]采用该方法成功地研究了晶体表面、晶界、表面吸附、表面偏析和空位缺陷等,都得到了非常令人满意的结果。

Cr之所以被本文选作辐照损伤的研究对象,是因为其多以化合态存在,键间强度大,熔点高,在电镀、制造特种钢以及未来的核反应堆材料中都具有很大的潜在应用。本文旨在研究Cr中哑铃(dumb-bell)间隙的稳定结构,从原子尺度上获得了哑铃间隙子(self-interstitial atom,SIA)在(001)和表面的能量 E;并计算了Cr中(110)和(111)哑铃SIA的形成能,得到(110)哑铃SIA结构最为稳定这一结论。其结果与用ab initio calculation和其他的理论或实验方法获得的结果基本一致。

本文采用MAEAM与MD模拟方法相结合的理论方法,鉴于该方法中的势函数形式较为简单,用其计算SIA能量和形成能都比用量子力学计算简单且计算精度高。而且该方法与第一原理等方法相比较起来,耗机时少,应用方便。

1 理论方法

1.1 MAEAM法

MAEAM法的基本公式[12]为:

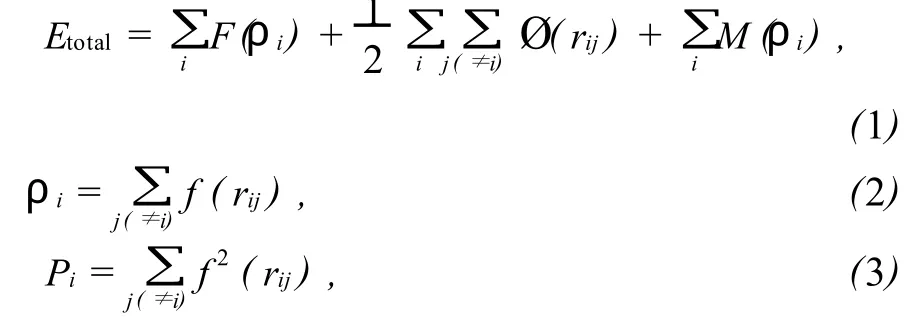
上式中:Etotal是系统的总能量;F(ρi)是在除第 i个原子外的其他原子组成的基体中再嵌入第i个原子的嵌入能,它仅是其他原子在第 i个原子所在处产生的背景电子密度ρi的函数,其中 f(rij)为单个孤立原子的球型电子密度分布函数;rij是第个原子和第j个原子间的距离;Ø(rij)是第 i个原子和第 j个原子间的相互作用能;M(ρi)是对最初嵌入原子法系统能量的修正,其中ρi为实际晶体中原子电子密度的非球型对称的贡献。

在计及更远近邻的情况下,嵌入函数 F(ρi)、原子间的相互作用能 Ø(rij)、能量修正函数 M(ρi)和电子密度函数 f(rij)分别为:

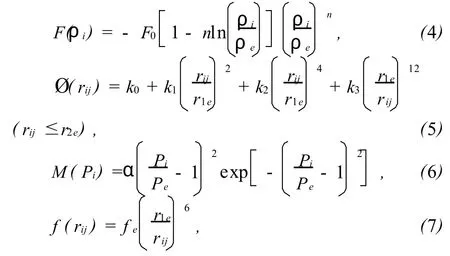
下标e表示平衡状态,r1e表示在平衡状态下纯元素晶体中原子的最近邻距离。本文选用的平衡状态的电子密度 fc为:

由能量与距离曲线拟合的 Rose公式,式(4)至(6)中的参数 n,α,F0,k0,k1,k2和 k3可根据所考虑BCC金属的结合能 Ec、单空位形成能 E1f、晶格常数a及弹性常数C11,C12和 C13分别由下列各式求得:

式(5)表示的相互作用势 Ø(rij)只适用于原子间距小于第2近邻 r2e的情况,对于距离大 r2e时,可使用一个三次条样函数作为截尾函数:式(16)中参数l0,l1,l2,l3和截尾距离 rc分别为:

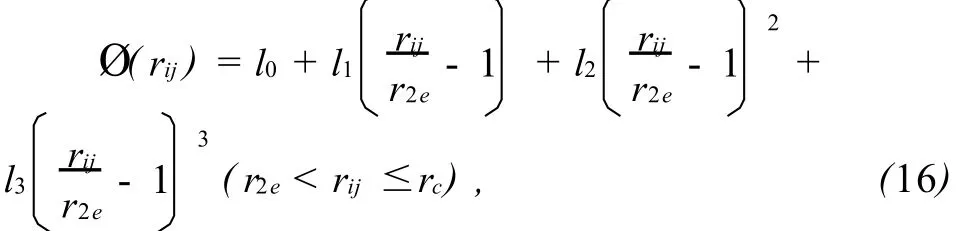
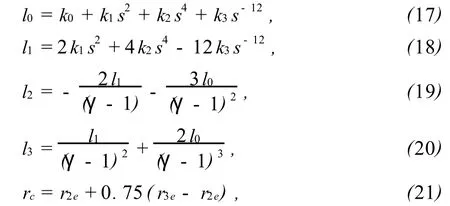
这里,r2e和r3e分别为平衡状态下第2近邻和第3近邻的距离

计算中Cr的输入参数为:晶格常数a=2.8845 Å,结合能 Ec=4.10 eV,单空位形成能 E1f=1.80 eV,弹性模量 C11=346 eV/nm3,C12=66 eV/nm3、C44=99 eV/nm3。Cr金属的有关参数的计算公式计算的MAEAM模型参数为:fe=0.3720 eV,n=0.8445,α=-0.3504,F0=2.3000 eV,k0=3.2012 eV,k1= -5.0749 eV,k2=3.0082 eV,k3=0.0276 eV,l0=1.6587 eV,l1=-0.5887 eV,l2=-0.2289 eV,l3=1.8506 eV。

1.2 计算过程

为了确保超晶胞中每个原子在相互作用势范围内具有完整的一系列近邻原子,本文选取具有559+1个原子的超晶胞,使其在模拟过程中能够不影响基体原子与SIA间的相互作用。

利用MD法研究由基体原子与SIA之间的相互作用所导致的晶格弛豫现象。晶胞中其它原子对第i个原子产生的作用力的α(分别为 x,y或z)分量可用下式计算:

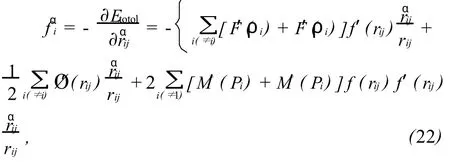
fαi为第 i个原子在α方向上的力和 rαij为原子 j与原子i之间的距离rij的α分量。弛豫后的SIA形成能EfI为:

t能量,Ec为结合能,用其来抵消附加的SIA能量。

2 结果与分析

由于SIA均处于平衡态晶体的对称面。故本文在立方结构的对称晶面群{100}和{110}中选取(001)和面作为对称面中的代表面,如图1所示,位置坐标以Cr的晶格常数a为基本单位。

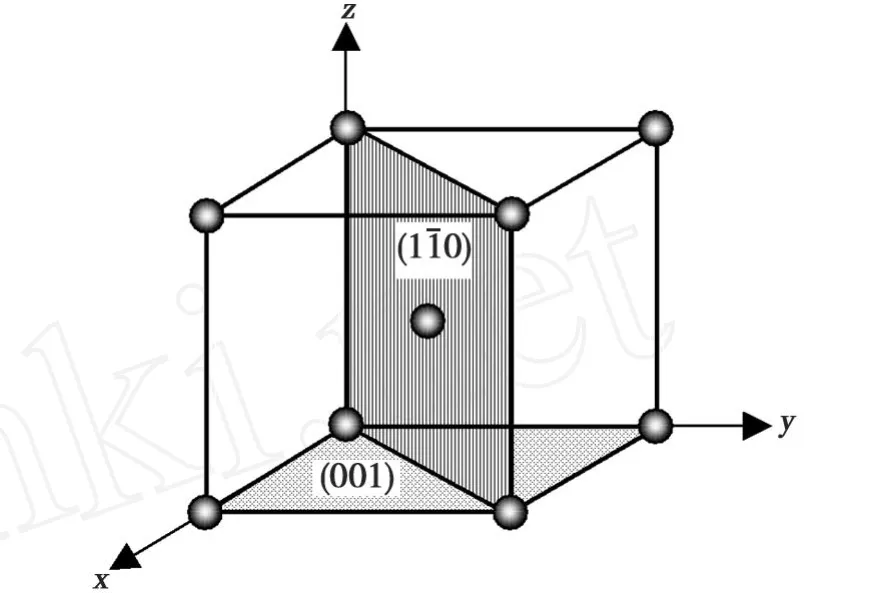
图1 扫描区域确定为含有哑铃SIA的代表面 (001)和面Fig.1 The scanning regions are defined as the representation plane(001)andcontaining either a dumbbell SIA interstitial

为了获得哑铃SIA在(001)和()表面的能量E的全貌,对哑铃SIA处在(001)和表面的任一位置进行全面扫描。考虑到晶体的对称性,故选取最小的扫描范围a＊a。首先将SIA放在原点位置,然后SIA以0.05Å的间隔分别沿着 x和 y轴方向移动,每移动一次计算出SIA的能量,获得的哑铃SIA处于(001)和表面扫描区域内任意位置的所有能量。可知,(110)和(111)哑铃SIA结构分别为SIA处于(001)和面的最稳定结构。为了便于描述,用S110和S111来表示(110)和(111)哑铃间隙位。(110)哑铃SIA结构为含有SIA晶体中的最稳定结构,(110)和(111)哑铃SIA处于(001)和面的能量最小值或局部最小值列于表1中。(001)和面的结构示意图。SIA到原点的距离在图2中标出,分别为0.509a和0.45a。

间隙缺陷的形成将会导致晶体中原子产生弛豫现象,晶格畸变是由间隙子附近的基体原子产生一系列的移动而形成的,是一个能量最小化过程。(110)哑铃SIA结构为含有SIA晶体中的最稳定结构

表1 哑铃自间隙子在(001)和面的能量最小值或局部最小值Tab.1 The minimum or local minimum values of the energy and corresponding positions of dumbbell interstitial on the(001)andplane

表1 哑铃自间隙子在(001)和面的能量最小值或局部最小值Tab.1 The minimum or local minimum values of the energy and corresponding positions of dumbbell interstitial on the(001)andplane

类型 (001)(110)Emin/eV -1.13(S110)3.58(S111)哑铃 (0.18a,0.18a,0)(-0.18a,-0.18a,0) (0.13a,0.13a,0.13a)(-0.13a,-0.13a,-0.13a)位置 (S110) (S111)

图2、图3分别为哑铃自间隙子S110和S111在Cr构,这是因为该结构具有最大的晶格空间和高对称性。本文在考虑弛豫问题的基础上计算出的Cr中哑铃自间隙的形成能和文献[17-19]计算出的哑铃间隙形成能均列入表2中,由表2可知,本文的计算结果4.05和4.76要小于 EAM的计算值 5.16[17]和5.78[18]和第一原理方法的计算值5.65[19],这说明本文所使用的MAEAM理论方法是可行的。

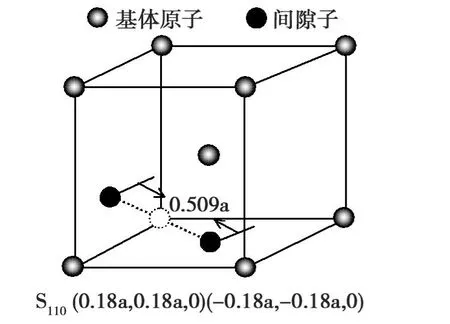
图 2 S110在 Cr 001面Fig.2 S110configurations for the Cr on the(001)surface

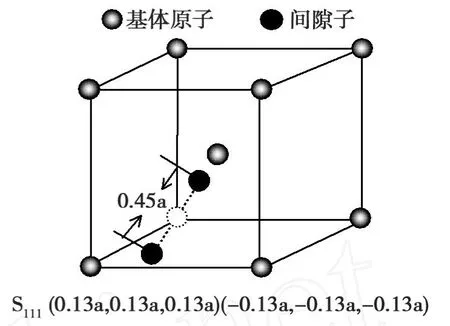
图 3 S111在 Cr 110面Fig.3 S111configurations for the Cr on thesurface

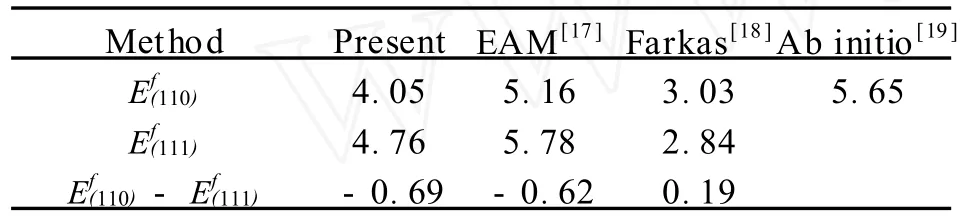
表2 哑铃自间隙子形成能 Efl eVTab.2 The formation energy Efl(eV)of the dumbbell SIA

3 结语

1)采用MAEAM与MD模拟方法相结合的理论方法计算SIA能量和形成能都比用量子力学的方法简单且计算精度高,且该方法与第一原理等方法相比较起来,耗机时少,应用方便。

[1]胡本英,木下博嗣,版口纪史,等.Fe-Cr-Mn钢时效析出碳化物的辐照损伤行为[J].金属学报,2006,42(3):234-238.

[2]Nolfi F V.Phase Transformations During Irradiation[M].New York:Applied Science Publishers,1983.

[3]Willians,Nelson G C.Surface Composition of Pt/Rh alloys[J].Applied Surface Science,1979,3:409.

[4]Van Langeveld A D,Niemantsverdriet J W.Surface composition of Pt-Rh alloys:The role of lattice vibrational entropy[J].Surface Science,1986,178:880-887.

[5]Ahmad M,Tsong T T.Compositional Variation in the Near Surface Layers,An Atom-Probe Study of Cosegregation of Sulfur in PtRh and PtIr Alloys[J].Journal of Chemical Physics,1985,83:388-396.

[6]Fu C C,Willaime F.Stability and Mobility of Mono-and Di-Interstitials inα-Fe[J].Physical Review Letters,2004,92(17):175503.

[7]Ulli Wolff.Collective Monte Carlo Updatingfor Spin Systems[J].Physical Review Letters,1989,62(4):361-364.

[8]García-Vidal F J,Pitarke J M,Pendry J B.Effective Medium Theory of the Optical Properties of Aligned Carbon Nanotubes[J].Physical Review Letters,1997,78(22):4289-4292.

[9]Weitao Yang.Direct calculation of electron density in density-functional theory[J].Physical Review Letters,1991,66(11):1438-1441.

[10]Domain C,Becquart C S.Ab initio calculations of defects in Fe and dilute Fe-Cu alloys[J].Physical Review B,2001,65(2):024103.

[11]Johnson R A.Analytic nearest-neighbor model for fcc metals[J].Physical Review B,1988,37(8):3924.

[12]邓辉球,胡望宇,舒小林,等.Pt-Rh二元合金系表面偏聚的分析型 EAM模型计算[J].金属学报,2001,37(5):467-471.

[13]王博,张建民,路彦冬,等.FCC金属表面能的各向异性分析及表面偏析的预测[J].物理学报,2010,60(1).

[14]Zhang J M,Huang Y H,Wu XJ,et al.Energy calculation for symmetrical tilt grain boundaries in iron[J].Applied Surface Science,2006,252:4936-4942.

[15]Zhang J M,Shu Y,Xu K W.Analysis of energy and force of Pt adatom on Pt(001)surface by MAEAM[J].Applied Surface Science,2006,252:5207-5214.

[16]Zhang J M,Wang Bo,Xu K W.Surface segregation of the metal impurity to the(100)surface of FCC metals[J].Pramana of Journal Physics,2007,69:603-616.

[17]Wallenius J,Abrikosov I A,Chakarova R,et al.Development of an EAM potential for simulation of radiation damage in Fe-Cr alloys[J].Journal of Nuclear Materials,2004,329-333:1175-1179.

[18]Farkas,D Schon,C GLima,M S F.et al.Embedded atom computer simulation of lattice distortion and dislocation core structure and mobility in Fe-Cr alloys[J].Acta Mater,1996,44:409.

[19]Christophe Domain.Ab initio modelling of defect properties with substitutional and interstitials elements in steels and Zr alloys[J].Journal of Nuclear Materials,2006,351:1-19.

Analysis of SIA Radiation Damage for
Cr by Modified Analytical Embedded-Atom Method

WANGBo1,LU Yandong2
(1 Key Laboratory of Ecophysics,Shihezi University,Shihezi 832003,China;2 Classroom Administration and Registration Division of Logistic Management,Shihezi University,Shihezi 832003,China)

From the atomic scale,dumbbell self-interstitial stable structure of Cr have been simulated and calculated by using the MAEAM and MD.The energies of the dumbbell SIA located in the(001)andsurface are attained,and the formation energy of the dummbell SIA is simulated.The results show that thedumbbell SIA stable structure in the(001)and(110)surface of Cr which have the lowest energies will be the most stable,which is consistent with the Ab initio calculation and other theory or experimental methods results.

Cr;MAEAM;MD;dumbbell;SIA

O77.1 < class="emphasis_bold">文献标识码:A

A

2010-07-05

王博(1982-),女,实验师,从事金属材料辐照损伤的研究;e-mail:xjrwbb1982@yahoo.com.cn。