具有年龄结构的SIRS流行病模型的分析
刘军军,闫萍,白江红
(新疆大学数学与系统科学学院,乌鲁木齐830046)
具有年龄结构的SIRS流行病模型的分析
刘军军,闫萍,白江红
(新疆大学数学与系统科学学院,乌鲁木齐830046)
建立和研究一类具有非终身免疫并带有年龄结构的SIRS流行病模型平衡解的存在性与稳定性。在总人口规模不变的假设下,运用微分方程和积分方程的理论和方法得到了决定疾病消亡与否的基本再生数 R0的表达式;证明了当 R0<1时无病平衡点是全局渐近稳定的,当 R0>1时此时至少存在一个地方病平衡点,并在一定的条件下证明了该地方病平衡点的局部渐近稳定性。
年龄结构SIRS流行病模型;基本再生数;无病平衡点;地方病平衡点;稳定性
流行病在现实生活中广泛存在,对流行病的研究已是数学知识应用的一个重要领域。目前,建立和研究年龄结构的流行病模型的工作有许多[1-6],但这些研究的都是具有终身免疫的年龄结构流行病模型。方彬等[7-8]研究了潜伏期和染病期均具有康复和传染的MSEIS流行病模型的稳定性,但模型没有考虑免疫期,因为有些疾病,例如鼠疫、白喉、炭疽、霍乱等许多流行病有暂时的免疫期,病人康复后先进入具有免疫力的移出者类,再以比例丧失免疫力而变成易感者。
靳祯[9]和Cooke虽然考虑了具有非终身免疫的传染病模型,但没有考虑年龄结构的因素。而年龄结构对传染病的影响是很重要的[11],因此,建立和研究非终身免疫且带有年龄结构的传染病模型具有重要的理论和实际意义。本文建立和研究具有非终身免疫且带有年龄结构的SIRS传染病模型,运用微分方程和积分方程的理论和方法讨论SIPR流行病模型平衡解的存在性与稳定性。
1 模型及其转化
把一个疾病传播的封闭社会的总人口分为三部分:易感类,染病类与康复类。首先引入一些记号:令 a和t分别表示年龄和时间,a+表示个体存活的最大年龄,分别用 S(a,t)、I(a,t)、R(a,t)、N(a,t)表示该社会时刻易感类、染病类、康复类和总人口关于年龄的密度函数,用b(a)和μ(a)分别表示年龄为的个体的出生率和死亡率,并假设b(a)和μ(a)不受疾病存在的影响,用c(a)表示年龄为的康复者失去免疫率,用α(a)表示年龄为 a的染病类进入康复类的比率。
本文不考虑疾病引起的死亡率,根据仓室建模思想得到具有非终身免疫并带有年龄结构的SIRS
流行病模型如下:
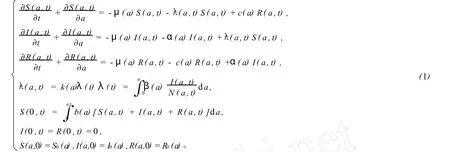
对系统(1)作如下归一化变换:
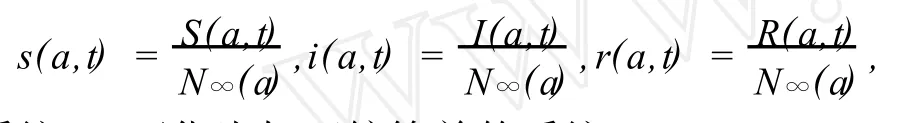
则系统(1)可化为如下较简单的系统:
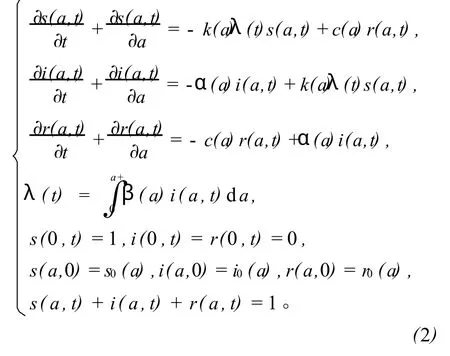
2 无病平衡点和地方病平衡点的存在性与稳定性
2.1 无病平衡点的存在性
设(¯s(a),¯i(a),¯r(a))为系统(2)的平衡点,则满足下面的方程组:
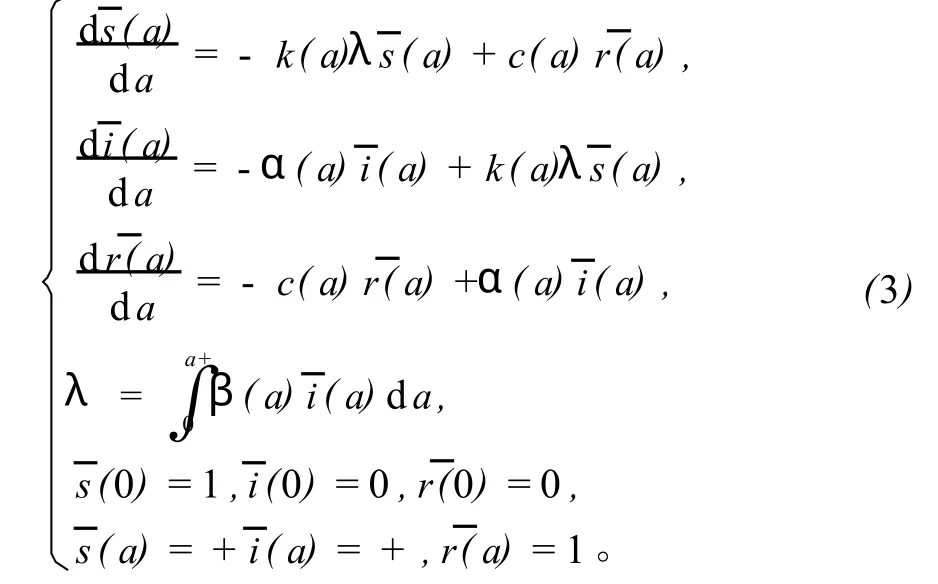
2.2 地方病平衡点的存在性
若系统(2)的平衡点 P*(s*(a),i*(a),r*(a))存在,即
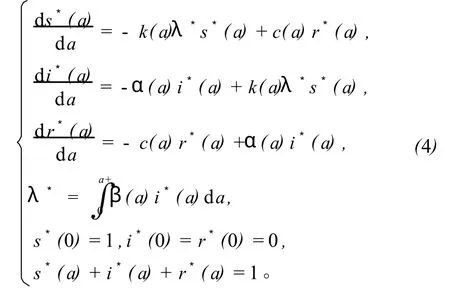
通过对方程组(4)求解得:a
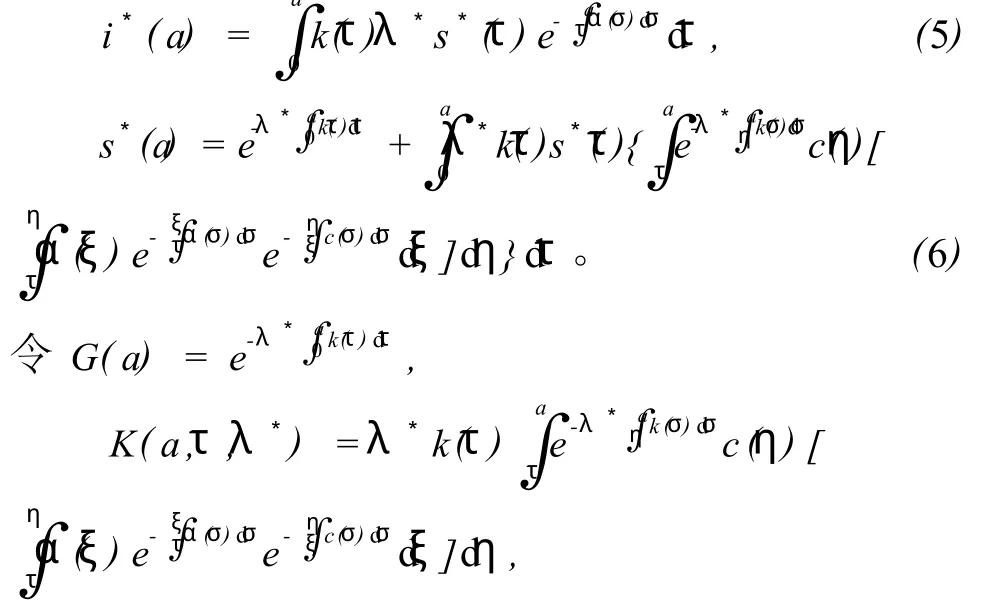
则方程(6)变为下列关于s*(a)的Volterra积分方程
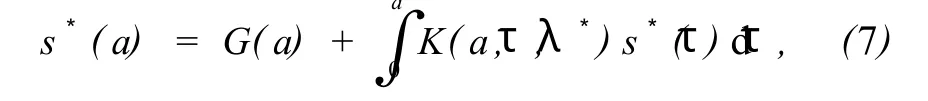
式(7)中,K(a,τ,λ*)是一个连续的 Volterra 核,对于每一个λ*,方程(7)都有唯一依赖λ*的解s*(a)。将式(5)代入方程组(4)的第4个方程得
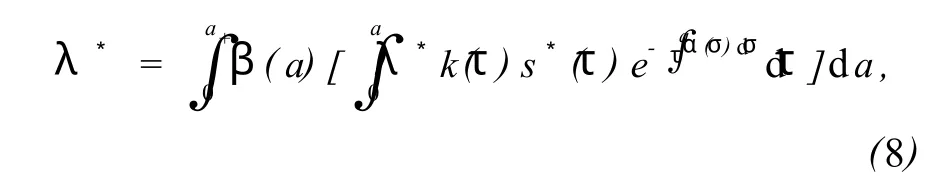
当λ*=0时,模型(2)有无病平衡解 P0(1,0,0),当λ*≠0时,有
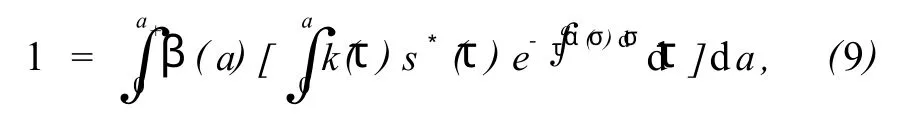
记式(9)右边为 H(λ*),则 H(λ*)是通过 s*(a)依赖于λ*的函数,令
这就是基本再生数的表达式,它表示一个典型的染病个体在其整个染病期间,在易感人群中所感染该种流行病的个体的平均数。
当 R0<1时,式(8)只有唯一解,相应的系统(2)只有唯一的无病平衡解 P0(1,0,0),当 R0>1时,即 H(0)>1。由式(5)及 i*(a)<1且有
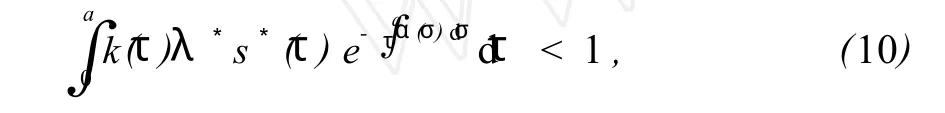
从而对任意的λ*>0,由式(9)和(10)得:
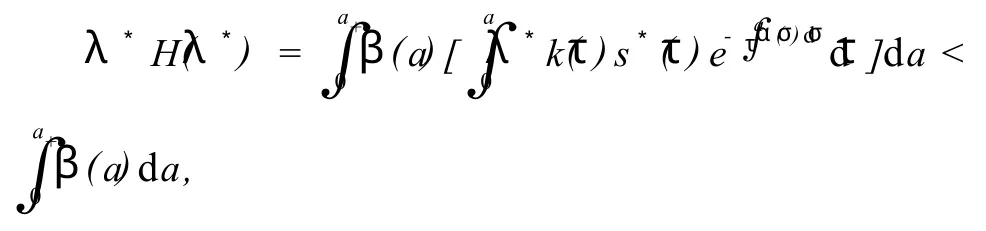
则当 R>1时,系统(2)除存在无病平衡点 P0(1,0,0)外,至少存在一个地方病平衡点 P*(s*(a),i*r*(a))。因此,有如下定理:
定理1当 R0<1时,系统(2)只有无病平衡解P0(1,0,0),当 R0>1时,系统(2)除无病平衡解 P0(1,0,0)外,至少存在一个地方病平衡点 P*(s*(a),i*(a),r*(a)) 。
2.3 无病平衡点的稳定性
定理2 当 R0<1时,无病平衡点 P0(1,0,0)是全局渐近稳定的;当 R0>1时,无病平衡点 P0(1,0,0)不稳定。
证明:为讨论无病平衡点 P0的局部渐近稳定性,将系统(2)在无病平衡点 P0处线性化,令并考虑到
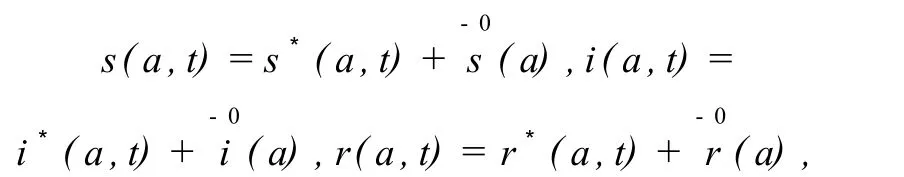
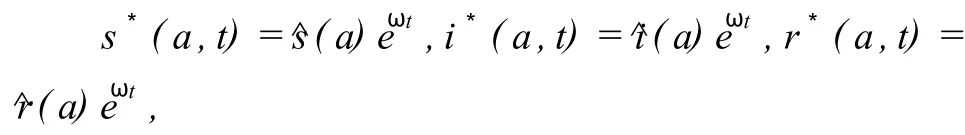
则函数^s(a)^i(a),^r(a)及参数ω满足下列方程:由系统(11)的第2个方程可得:
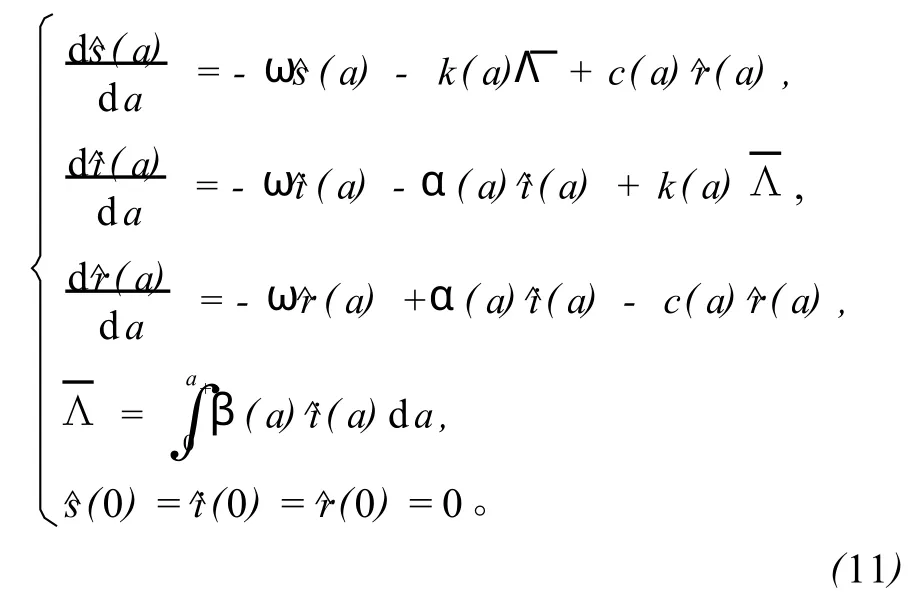
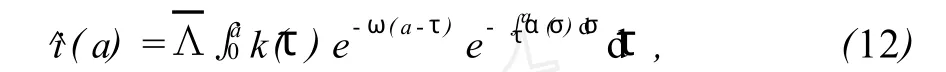
把式(12)代入系统(11)的第4个方程得:
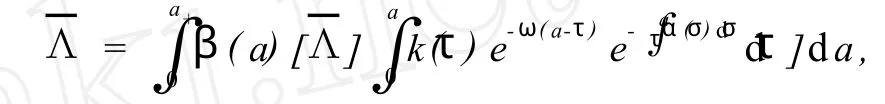
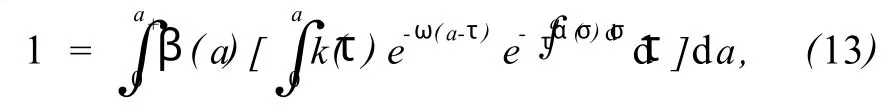
对于式(13),当ω取实数时有:
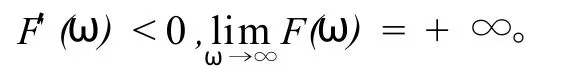
于是,函数 F(ω)在(-∞,+∞)上是严格单调递减函数,当且仅当 R0<1(即 F(0)<1)时,方程(13)存在唯一的负实数根ω*;当且仅当 R0>1时,方程(13)存在唯一的正实数根。故当 R0<1时特征方程(13)只有负实部特征根,当 R0>1时,特征方程(13)有正实部的特征根。由此得到,当 R0<1时,无病平衡点是局部渐近稳定的。当 R0>1时,无病平衡点不稳定。
为了得到全局渐近稳定性,对系统(2)的第2个方程沿特征线积分得:(14)当 t>a时,把式(14)代入系统(2)的第5个方程得:
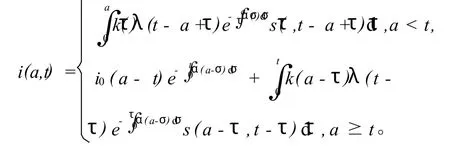
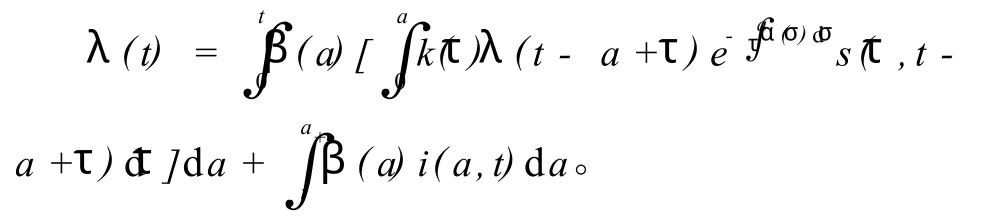
-0同时有s(a,t)≤1=s(a),故且有
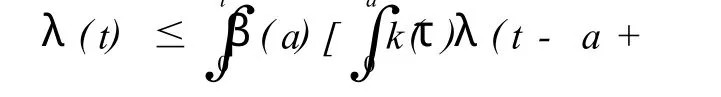
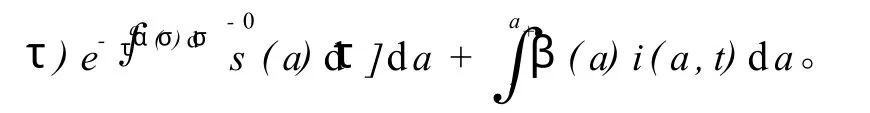
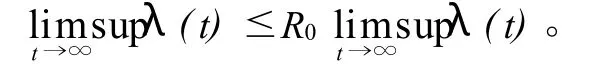
由于 R0<1,故只有令由式(14)知:
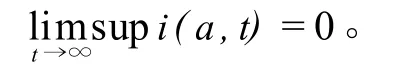
对方程(2)的第3个方程沿着特征线积分并利用Fatou引理得:
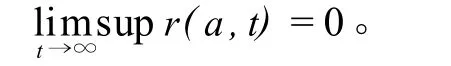
2.4 地方病平衡点的稳定性
为了讨论地方病平衡点 P*(s*(a),i*(a),r*(a))的稳定性,首先对系统(2)在 P*点处线性化,令
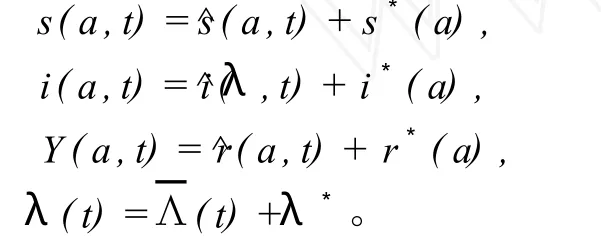
并考虑到:
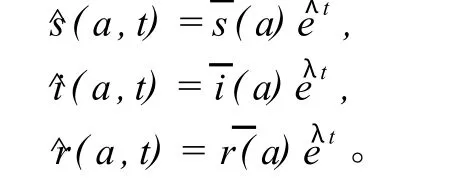
为了讨论方便,假设Λ≠0,令:
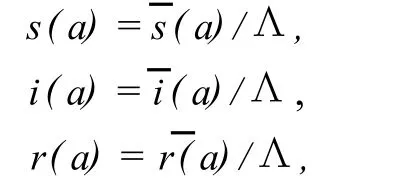
则系统(2)可化为
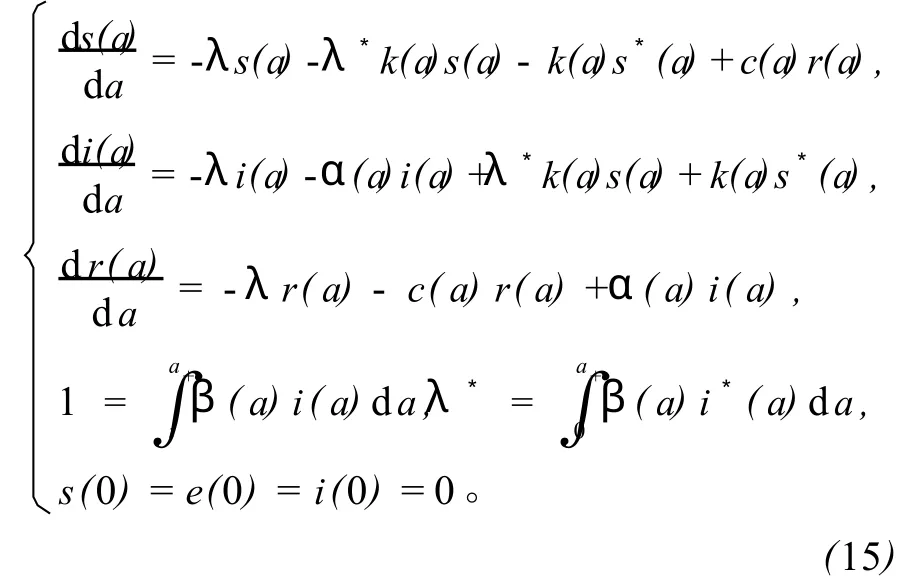
把系统(15)前三个方程相加,并考虑边界条件得:s(a)+i(a)+r(a)=0。
由系统(15)的前三个方程分别得:
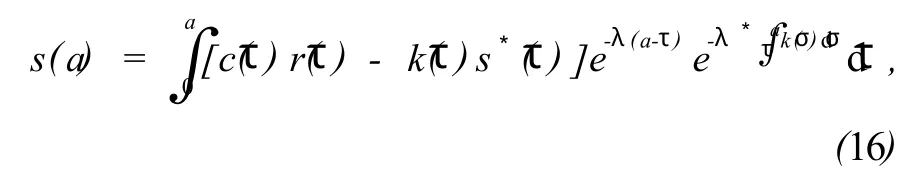

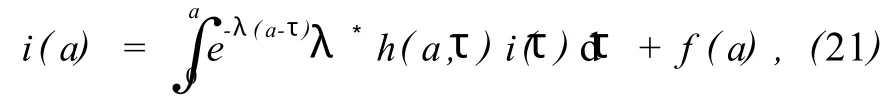
显然 h(a,τ)和 f(a)是与参数λ无关的非负函数,且方程(21)为关于 i(a)的Volterra积分方程,由文献[12]知积分方程(21)有以下解:
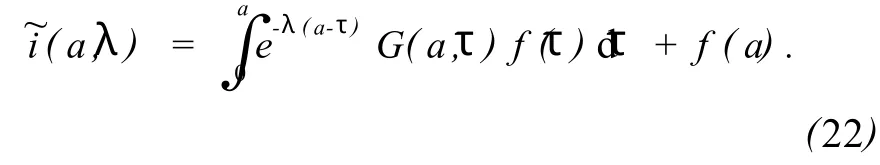
式(22)中 G(a,τ)是与参数λ无关的非负函数。

定理3:若假设式(20)成立,则有:
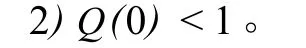
证明:1)由于
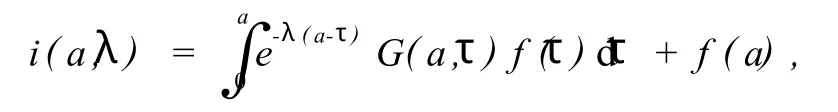
把 ¯i(a,λ)代入式 (23),整理后得 :
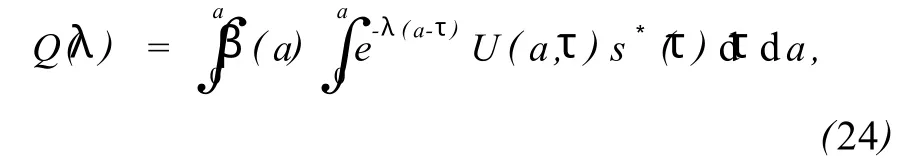
其中U(a,τ)=k(τ)g(a,τ)+∫aτG(a,η)k(τ)g(η,τ)dη。由前面假设知:U(a,τ)(对 0≤τ≤a≤a+)是与参数λ无关的非负函数。所以由方程(24)知 Q(λ)≥0,并且 Q(λ)是关于 x的递减函数,故当λ→+∞时,Q(λ)→0。
2)把式(17)代入 Q(λ)的表达式,当λ=0时,
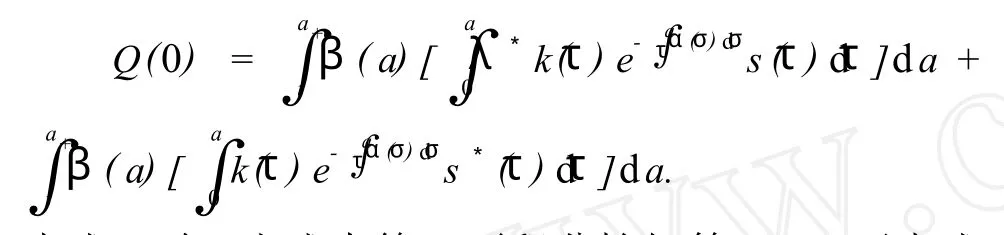
由式(9)知:上式中第2项积分恰好等于1。再由式(20)知:
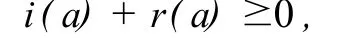
又因为
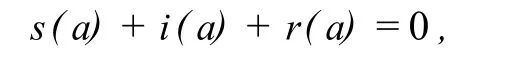
故可得s(a)≤0,∀a∈[0,a+],从而上式第1项积分为负。
综上所述,所以有 Q(0)<1。
由定理3知,在式(20)的假设下,若 R0>1,则特征方程(23)只有负实部的根,从而地方病平衡点是局部渐近稳定的。因此有如下定理:
定理4:当 R0>1时,若式(20)满足,则地方病平衡点 P*是局部渐近稳定的。
3 结论
本文建立和讨论了具有非终身免疫且具有年龄结构的SIRS流行病模型,得到了基本再生数 R0的表达式,证明了当 R0<1时,无病平衡点是全局渐近稳定的,当 R0>1时,无病平衡点不稳定,此时系统至少存在一个地方病平衡点,并在一定条件下证明了该地方病平衡点时局部渐近稳定的。当 R0>1时,是否存在多个地方病平衡点以及地方病平衡点是否为全局渐近稳定的仍是一个有待解决的问题。
[1]Hoppensteadt F.An age-structured epidemic mode[J].Franklin Inst,1974,197:325-333.
[2]Inaba H.Threshold and stability results for an agestructured epidemic model[J].Math Biol,1990,28:411-434.
[3]Li X Z,Geni Gupur,Zhu G T.Threhold and stability results for an age-structured SEIR epidemic model[J].Comp Math Appl,2001,42:883-907.
[4]Li X Z,Gupur Geni,Zhu G T.Analysis for an Agestructured SEIR Epidemic Model with Vaccination.Inter[J].Diff Equ Appl,2003,7(1):47-67.
[5]Li X Z,Gupur Geni,Zhu G T.Existence and Uniqueness of Endemic State for the Age-structured SEIR Epidemic Model[J].Acta Math Appl,2002,18(3):441-454.
[6]荣翠贤,盛其荣.一类传染病动力学偏微分方程组解的适定性[J].石河子大学学报:自然科学版,2007,25(2):251-255.
[7]方彬,李学志.潜伏期具有传染性的年龄结构MSEIS流行病模型的稳定性[J].应用数学学报,2008,31(1):110-125.
[8]方彬,杨金根,李学志.潜伏期和染病期均具有康复的年龄结构MSEIS流行病模型的稳定性[J].应用数学,2009,22(1):90-100.
[9]靳祯.在脉冲作用下的生态和流行病模型的研究[D].西安:西安交通大学,2001:34-65.
[10]Cooke K L,Driessche P Van Den.Analysis of an SEIRS epidemic model with two delays.J Math Biol,1996,35:240-258.
[11]马知恩,周义仓,王稳地,等.传染病动力学的数学建模与研究[M].北京:科学出版社,2004:335-393.
[12]Gripenberg G,Londen S,Staffans O.Volterra Integral and Functional Equation[M].Camberidge:Camberidge Univ Press,1990:145-150.
An SIRS Epidemic Model with an Age-Structured
LIU Junjun,YAN Ping,BAI Jianghong
(College of Mathematics and Systems Science,Xinjiang University,Urumqi 830046)
An SIRS epidemic model with an age-structured is studied.By using the theory and methods of Differential and Integral Equation,the explicit expression of the basic reproductive numberR0was obtained.It is showed that the disease-free equilibrium is locally and globally asymptotically stable ifR0<1,at least one endemic equilibrium exists ifR0>1,the stability conditions of endemic equilibrium are also given.
age-structured SIRS epidemic models;the basic reproductive number;the disease-free equilibrium;endemic equilibrium;stability
O175.12 < class="emphasis_bold">文献标识码:A
A
2010-09-29
新疆高校科研重点项目(XJ EDU2007I03)与创新团体项目(XJ EDU2007G01)
刘军军 (1984-),男,硕士研究生,专业研究方向为偏微分方程理论及应用;e-mail:liujunjun㊦0517@163。com。

