扩散方程的一种跳点格式
马菊香
(石河子大学师范学院数学系,石河子832003)
扩散方程的一种跳点格式
马菊香
(石河子大学师范学院数学系,石河子832003)
通过求解泥沙扩散方程研究泥沙沿水深的分布和含沙量分布沿程的变化规律,构造了一种新的差分格式——跳点格式,并对其理论性质作了分析验证,结果表明:这种格式计算简便,算法简单,稳定性好、精度较高,体现了这种格式的实用性和优越性。
扩散方程;差分格式;稳定性
1 泥沙扩散方程的新的差分格式及算法
1.1 差分格式的构造
泥沙扩散方程经过一定程度的简化和变形,可以化为如下的微分方程[1]:
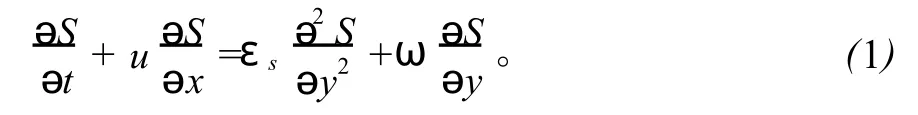
偏微分方程(1)是一个二维变系数的抛物型方程,对于多维方程,显格式稳定性要求很高,隐格式虽然稳定性较好,但要解大型的代数方程组,并且这些方程组又不是三角形方程组,工作量也非常大。为了克服上面2种格式的不足,笔者建立了一种实用的跳点格式。
为了对扩散方程(1)建立差分格式,先引入差分算子[2-3]:
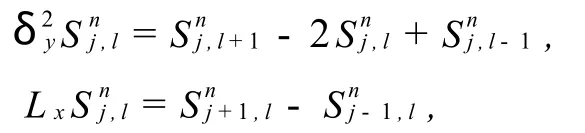
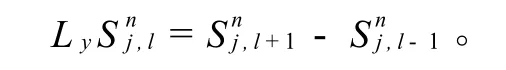
对方程(1)先构造显式差分格式,有:
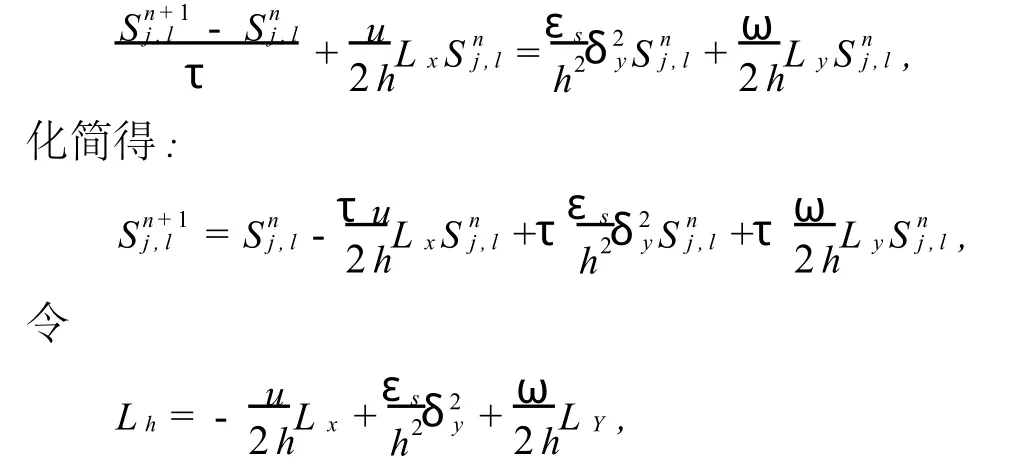
则上式显格式可以化简为:

相应地,其隐格式为:
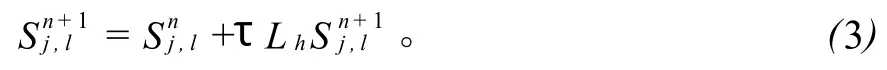
对显、隐格式(2)、(3)引入一个奇偶函数[4]
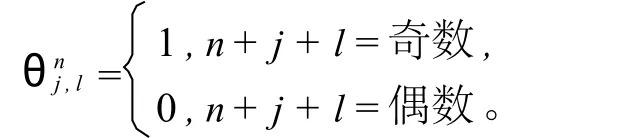
可以对(1)建立跳点格式[5-6]为:
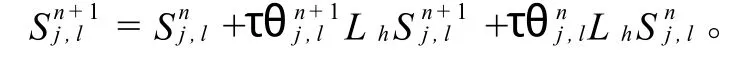
1.3.1 相容性分析
对式(11)进行 Taylor展开,可得到
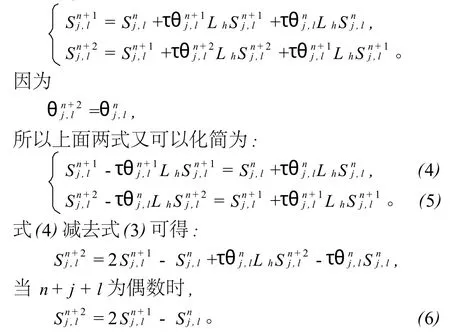
由上式可知:在相邻的时间层上,对固定的空间点(xj,yt)上的算法是改变的。下面给出相邻时间层上的计算公式:
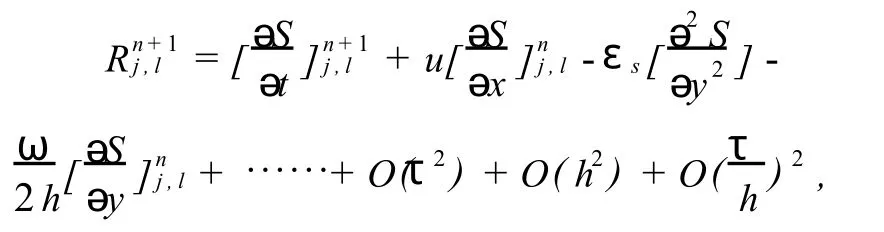
由此可看出,相容性就要求当τ→0,h→0时,τ/h→0,即差分方程与微分方程相容的充分必要条件是:τ→0的速度比 h→0的速度快,使τ/h→0,反之,若τ/h不趋向0,那么差分方程就不与扩散方程相容了,所以跳点格式是条件相容的。
1.3.2 稳定性分析
由于式(10)是一个三层格式,因此首先把它化成与其等价的二层差分方程组:
1.2 跳点格式的算法
设在第 n层上,Snj,l已知,求 n+1层上的 Sn+1j,l值有以下三步:

第3步:在上面的基础之上,代入式(6)即可求出n+2时间层上的值。
由上可见,这种跳点法非常节省工作量。
1.3 相容性和稳定性的理论分析
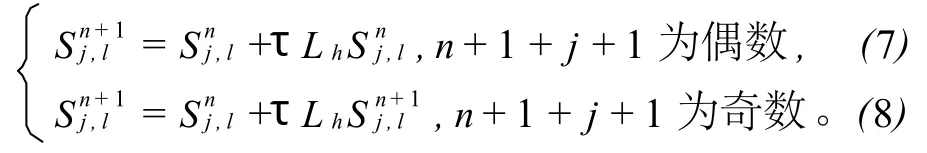
跳点格式
当利用式(8)算出奇数网格点上的Sn+1j,l时,n+2+j+l必为偶数,此时利用式(7)可以得到
式(8)与(7)相减得到:
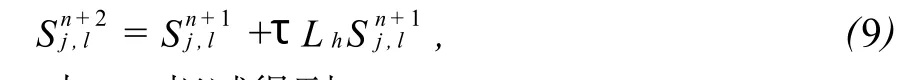

式(10)中,n+2+j+l为偶数。
从式(10)与(8)中消去 Sn+1j,l可以得到:
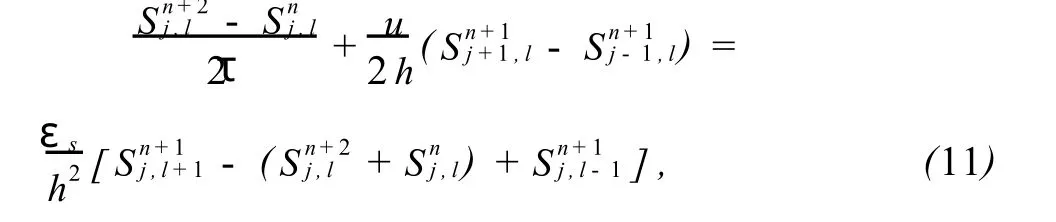
下面给出增长矩阵 G的特征值估计,为此引入一个引理,即
Miller定理[8]:若 G的特征方程为Aλ2+Bλ+C=0,则 G的特征值λ满足
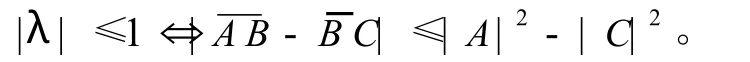
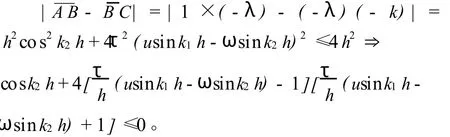
由于,τ≤≤h,且参数 u,ω的取值远远小于1,所以在上面的情况下,在差分格式相容的条件下,对于任意的τ和h,此式是绝对成立的。
定理:跳点格式是一个条件相容、绝对稳定的差分格式。B=-λ,C=-k,根据上面的定理,下面验证(10)的稳定性。经计算的一般规律:水面浓度相对较小,近底浓度相对较大,含沙量沿程衰减的特性较为明显。在距进口300 m处,泥沙的分布调整到一种不平衡输沙状态,随着泥沙的沿程淤积,水流输沙向平衡方向发展,垂线平均含沙量趋于水流挟沙力,而含沙量沿垂线分布向平衡时的分布状态发展。计算结果表明,本文提出的计算方法是合理可行的。
2 实例及分析
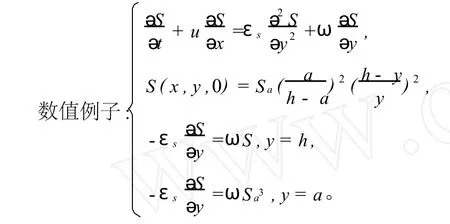
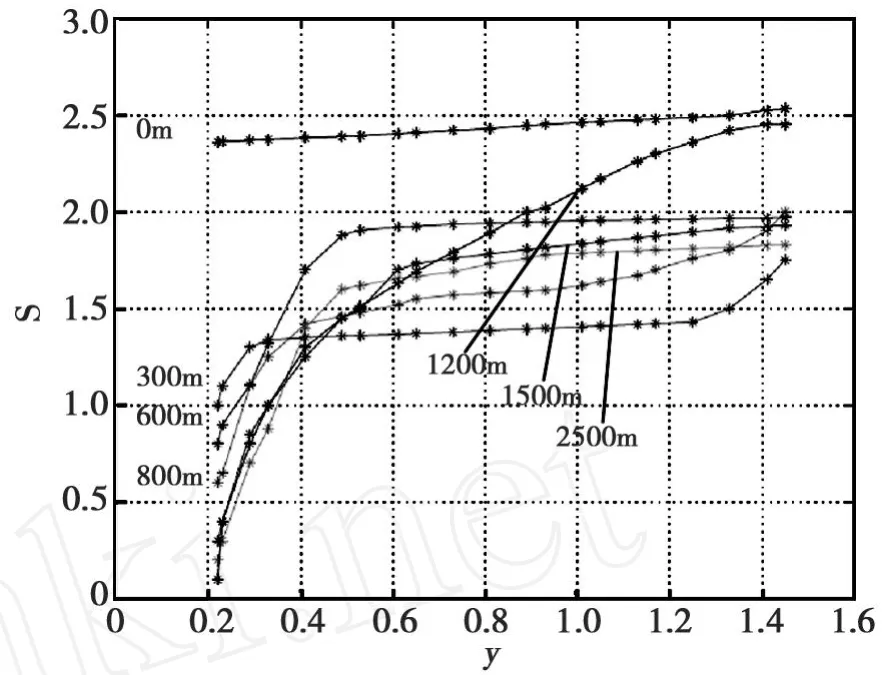
图1 数值模拟结果Fig.1 figure of numerical result
其中参数的确定参见文献[1]。
用跳点格式对上面的例子进行模拟,主要数据为:水深 h=1.53 m,平均流速 u=0.12 m/s,泥沙沉速ω=0.0176 cm/s,悬浮指标z=0.01,计算时取卡门常数 k=0.4,a=0.05h。
图1是用跳点格式的数值模拟结果,其中 y表示相对水深,S表示沿水深含沙量的变化规律,曲线旁的数字表示断面距进口的距离。
由图1可见,计算结果符合含沙量沿垂线分布
图2是用Douglas差分格式和交替方向隐格式模拟出的曲线变化。
由图2可知,本文的跳点格式比Douglas差分格式计算精度高,更加符合泥沙沿程变化规律,且光滑性较好;而与交替方向隐格式比较,后者需要求解大型的代数方程组。
本文构造的跳点格式实质上是一个显式算法,简单易算,其计算量要远远小于交替方向隐格式,并且模拟效果很好。
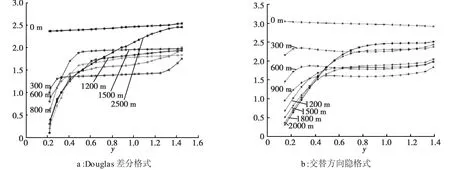
图2 不同格式模拟出的泥沙沿程变化Fig.2 Changes along the river simulated by different patterns
3 结论
本文在显、隐格式的基础上加入了一个0-1函数,把节点分为奇、偶两组点分别计算,构造了它的跳点格式。经过理论分析和实例验证,跳点格式在计算上比交替方向隐格式要简单易算,在精度上要比Douglas差分格式[9]高,是一个实用有效的计算格式。
[1]马菊香,阿不都热西提.阿不都外力.剖面二维非恒定悬移质泥沙扩散方程的数值方法[J].新疆大学学报:自然科学版,2007,24(2):171-174.
[2]马菊香.泥沙扩散方程的Douglas差分格式[J].通化师范学院学报,2008,29(10):7-8.
[3]张杰,李永红.平面二维河床冲淤计算有限体积法[J].长江科学院院报,2002,19(5):17-20.
[4]陈焕帧.平面二维水沙模型的特征有限元数值模拟[J].高等学校计算数学学报,2007,29(3):245-256.
[5]梁国亭,高懿堂,等.非恒定流泥沙数学模型原理及其应用[J].泥沙研究,1999(4):44-48.
[6]韩其为,胡春宏.50年来泥沙研究所主要研究进展[J].中国水利水电科学研究院学报,2008,6(3):170-182.
[7]陆金甫,关治.偏微分方程数值解法[M].北京:清华大学出版社,1987.
[8]崔侠.剖面二维数学模型的研究[D].武汉:武汉水利电力学院,1988.
[9]胡健伟,汤怀民.微分方程数值方法[M].北京:科学出版社,1999.
A Jumped Node Different Format of Diffusion Equation
MA Juxiang
(Department of Mathematics,Teachers College,Shihezi University,Shihezi,832003,China)
In this paper,through solving sediment diffusion equation to study the distribution of sediment concentration along with depth,creating a new difference format—a jumped node different format.The theory of its nature and analyzed validation:This method is simple and convenient,highly accurate and stable.This format embodies practicability and superiority.
diffusion equation;different format;stability
O241.82 < class="emphasis_bold">文献标识码:A
A
2009-07-26
马菊香(1979-),女,讲师,从事偏微分方程数值解研究;e-mail:majuxiang@shzu.edu.cn。

