论莫尔条纹的计算

龚仲华

(常州机电职业技术学院，江苏常州 213164)

光栅是数控机床等机电一体化设备常用的位置检测装置，其工作原理早为人们所熟知。一次偶然的机会，笔者发现某高校教材中所给出的莫尔条纹节距计算式存在错误，因而专门浏览了其他教材及相关参考书，不料这样的错误竟然十分普遍，乃至于未见正确的计算式。为此，本文将对光栅莫尔条纹的正确计算式进行分析与证明，以供读者参考。

1 问题的提出

众所周知，绝大多数光栅都是通过如图1b所示的夹角为θ的标尺光栅与指示光栅所产生的莫尔条纹来放大栅距W(光栅的条纹间距)、提高测量分辨率的，因此，分析光栅工作原理需要确定莫尔条纹节距B与光栅栅距W、夹角θ的关系问题。归纳目前教材与参考书中所提供的莫尔条纹节距B计算式，主要有以下3种:

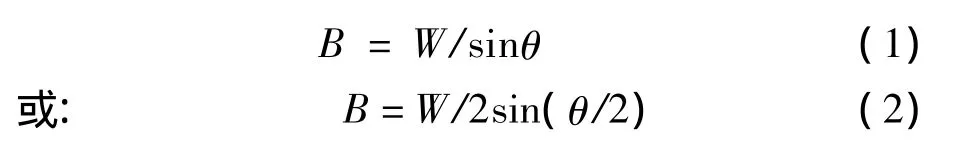
式(1)［1－2］与式(2)［3－4］为标尺光栅与指示光栅在栅距同为W时的计算式;部分书籍还提供了指示光栅栅距为a、标尺光栅栅距为b时的计算式［5－6］:

以上3个计算式都是错误或片面的。

从图1b可见，式(1)误将倾斜条纹被相邻两垂直条纹所截线段(图1b中的粗线段)的长度直接当成了莫尔条纹的节距B，这显然不正确。

式(2)已注意到这一问题，它在计算式(1)的基础上通过三角函数变换，由B=(W/sinθ)·cos(θ/2)=W/［2sin(θ/2)］得到结论。如仅从图1b上看，这一结论似乎是正确的。但是，如进一步分析当两光栅夹角θ=180°时的情况，此时由于两光栅相互平行，实际上不可能得到上下移动的莫尔条纹，但按计算式(2)得出的结果为B=W/2，这就意味着光栅能生成节距为W/2的莫尔条纹，此结论显然与实际情况不符。

由下面的分析可知，式(3)所提供的莫尔条纹节距计算式是不正确的。

2 分析要点

以上计算式错误的原因在于，他们没有根据莫尔条纹产生的一般规律来分析问题，所得到的结论或只适用于特定情况或存在错误，因此，不能正确解释莫尔条纹的普遍现象。

计算莫尔条纹节距B必须先计算莫尔条纹的水平夹角α(图2)，即确定条纹的运动方向，这是分析问题的关键。因为，α一旦为90°，条纹就不再有垂直方向的上下运动，节距也就失去了意义。

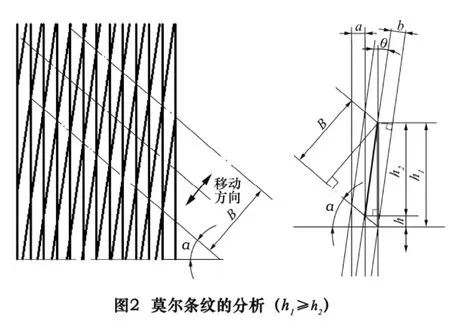
莫尔条纹的节距B、夹角α不但与两光栅的夹角θ有关，而且还与光栅的栅距有关。栅距不同的光栅同样可以生成莫尔条纹，这一点在分析时同样必须清楚。莫尔条纹夹角α的分析方法如下:

假设倾斜条纹的宽度为b、垂直条纹的宽度为a，从图2可以得到垂直条纹被相邻两倾斜条纹所截部分的长度h1为

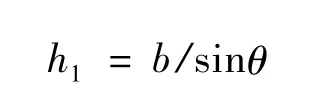
倾斜条纹被相邻两条垂直条纹所截部分在垂直方向的投影长度h2为

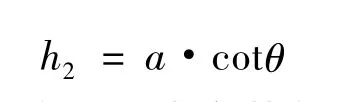
h1与h2之间的关系是决定莫尔条纹水平夹角α、节距B的关键，必须由此入手，通过对不同情况的分析，才能得到正确结论。

3 正确的计算式

莫尔条纹的节距B、夹角α与h1、h2有关，在不同情况下的计算式可以推导如下。

3.1 h1≥h2

当h1≥h2时，莫尔条纹的情况如图2所示，因此有:

即莫尔条纹的节距B与垂直条纹宽度b直接相关。

由式(5)可见，若光栅夹角 θ=0°或180°，则夹角α为90°，故无垂直方向移动的莫尔条纹;或简单地从式(6)上理解为B=∞，这也可解释无莫尔条纹的实际情况。

对于a=b的特殊情况，可得到:

由此可见，式(2)仅是在特殊情况下所得到的特殊结论，而不能用来解释普遍现象。

3.2 h1＜h2

h1＜h2时的情况较为复杂，分析如下。

① 如h1＜h2≤2h1，其情况如图3所示，计算方法如下:

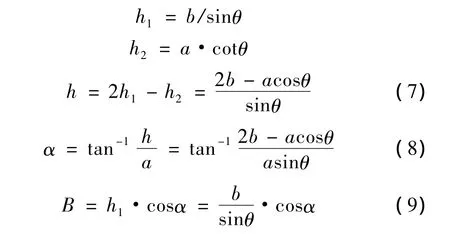
即:莫尔条纹的节距B与倾斜条纹宽度b直接相关。式(8)与式(9)同样可以解释θ=0°或180°两种特殊情况。

对于a=2b的特殊情况，则存在以下结论:

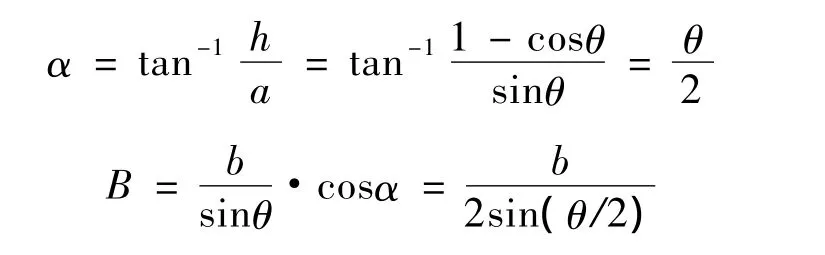
与a=b的情况相比，这时所产生的莫尔条纹其水平夹角α不变，但节距B是a=b时的1/2(图4)。

②对于栅距相差更大的光栅，同理可推出其计算式。如2h1＜h2≤3h1，则:

同样对于a=3b的特殊情况，这时所产生的莫尔条纹水平夹角仍然为θ/2，但节距B是a=b时的1/3。依次类推，可得出3h1＜h2≤4h1等情况下的结论。以上结论可以直接通过实验证明，也可以简单地用CAD制图进行模拟验证。

4 结语

光栅莫尔条纹的分析与计算只需要简单地利用三角函数便可进行，特别是在CAD技术普及的今天，还可用CAD直接进行验证，因此，在教材、设计手册等较为严肃的参考书籍中，还是有必要进行深入、仔细的分析，以防止出现基本概念上的错误而误导读者。

［1］何玉安.数控技术及其应用［M］.北京:机械工业出版社，2004.

［2］上海市电气自动化研究所.机床数字控制与计算机应用［M］.北京:机械工业出版社，1982.

［3］王永章.数控技术［M］.北京:高等教育出版社，2001.

［4］张燏.机电一体化概论［M］.北京:人民邮电出版社，2009.

［5］赵先仲.机电系统设计［M］.北京:机械工业出版社，2004.

［6］李谋.位置检测与测量技术［M］.北京:机械工业出版社，1991.